Kaj je egiptovski sistem številk? Zgodovina, opis, primeri

Z nenasilnim egiptovskim številskim sistemom, ki je bil uporabljen v starem Egiptu, smo vizualno seznanjeni z nekaj preostalimi papirusi. Primeri nalog in njihovih rešitev so v njih tako zanimivi, da ostane le obžalovanje, da jih je tako malo.

Iz njih je razvidno, da sta bila matematika in egiptovski sistem številk tesno povezana z gospodarskimi potrebami in praktično uporabo. Vsako leto po poplavi Nila je bilo treba obnoviti stavbe, ponovno zemljišča, izračunati površino in meje, voditi evidenco o žetvi, koledarju.

Kaj so pozicijski in ne-pozicijski oštevilčeni sistemi?

Odgovor leži v samem naslovu. Če položaj številke vpliva na rezultat izračunov, imamo pozicijski sistem števil, če ne - ne pozicijski.

Če pišemo 12, to je dvanajst, in z enakimi številkami, je 21 enaindvajset. V skladu z egiptovskim sistemom številk: za pisanje 12, morate uporabiti simbol enote dvakrat in desetkratni simbol enkrat, 21 pa bo izgledal kot enojni simbol in dva desetkovna simbola, kar pomeni, da morate samo napisati tri simbole.

Nepolicijske so: rimski sistem, ki nam je znan, v katerem so številke označene z rimskimi črkami, slovanskim sistemom, kjer vsaka črka označuje tudi določeno število ali številko. Rimski sistem se je do 16. stoletja soočal s svojimi funkcijami v zahodni Evropi.

Številski sistem, ki ga uporabljamo v sodobnem življenju, je pozicijski decimalni sistem.

Nonpositional sistemi so bili zelo primerni za opravljanje enostavnih aritmetičnih operacij, saj so kompleksni izračuni vključevali okorne zapise, ki niso preprečevali uspešnega razvoja algebre in geometrije v starem Egiptu.

Kako so Egipčani mislili?

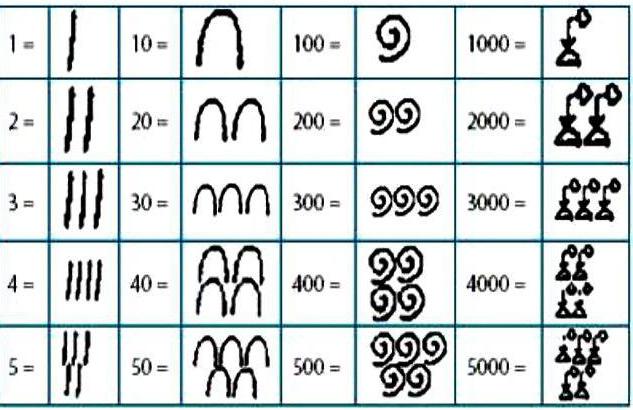
Kaj je to - egiptovski sistem številk? Za pisanje poljubnega števila smo uporabili hieroglife, ki označujejo določene številke, katerih vsota je bila enaka želeni vrednosti.

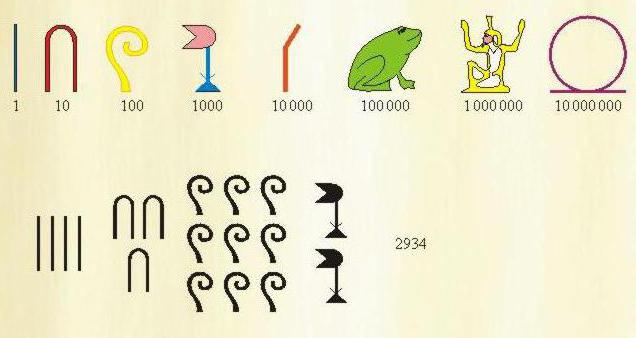
Na voljo so bile posebne oznake za številke 1, 10, 100, 1000, 10000, 100000, 1000000. Pri pisanju zahtevane številke je bila vsaka oznaka uporabljena do 9-krat. Zapis v egiptovskem številčnem sistemu je bil v naraščajočem zaporedju: najprej enote, nato desetine, stotine in tako naprej.

Praviloma so pisali od desne proti levi, vendar je bilo od leve proti desni možno, da se znesek tega ni spremenil. Uporabljeno je bilo tudi vertikalno pisanje, potem pa je odštevanje odšlo od zgoraj navzdol.

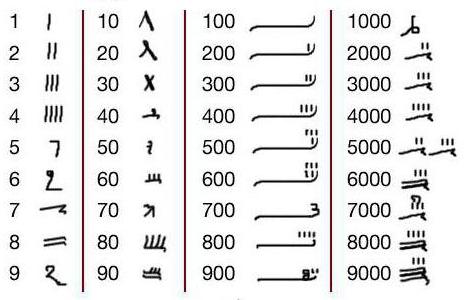
Uporabljena sta bila dva načina pisanja:

1. Hieroglyphic, v katerem so bili uporabljeni sprejeti hieroglifi.
2. Hieratic, ki je bil bolj shematičen in primeren v praksi.

Ogled zgodovine

Zgodovina egiptovskega številskega sistema je nastala v antičnih časih, prvi rokopisi s številkami pa se nanašajo na drugo tisočletje pr. Denarja potem ni bilo, zato je bil sistem uporabljen tako za neverjetno kompleksnost in velikost matematičnih problemov kot tudi za reševanje vsakodnevnih vsakodnevnih problemov.

Navsezadnje je bilo poznavanje matematike uporabljeno pri geodetskih posegih ter pri gradnji koledarjev in zemljevidov v astronomiji, plovbi in gradnji palač, kanalov in vojaških utrdb.

Egiptovski ne-pozicijski sistem je bil uporabljen do 10. stoletja.

Imela je tudi mističen pomen, skrivnost, ki so jo duhovniki vzeli s seboj, deloma pa je odprl svet Pitagori. Ima dela, v katerih opisuje simbolne pomene, ki jih dajejo digitalni hieroglifi, ki jih je napisal po svojem bivanju v Egiptu. Zato njihov opis pripada egiptovskemu številskemu sistemu.

Preživelo je le nekaj papiranj tistih časov, s katerimi je mogoče razumeti, da je bila raven matematike visoka. Avtentično je znano, da so Grki preučevali starodavno egiptovsko matematiko. Eno od najglobljih znanj je egiptovski ne-pozicijski sistem številk.

Papyrus Ahmes

Akhmes Papyrus sega v leto 1650 pred našim štetjem in vsebuje 84 matematičnih nalog. Najdeno je bilo v Tebah, shranjenih v Britanskem muzeju.

Vse naloge v papirusu obravnavamo na konkretnih primerih egiptovskega številskega sistema. Prikazujejo primere izračunov z ulomki, s celimi števili, delitvijo in množenjem.

Podani so izračuni za iskanje področij geometrijskih oblik: štirikotnik, krog, trikotnik.

Informacije iz papirusa dokazujejo, da so egiptovski matematiki lahko izvlekli koren, naredili aritmetiko in geometrijsko napredovanje enačbe z neznankami.

Alikvotne frakcije

Zanimivo je, da so bile v izračunih uporabljene samo alikvotne frakcije, pri katerih je bil števec enak enemu in je bil označen s takšnim znakom, pod njim pa so bile zapisane vrednosti imenovalca, vse druge frakcije za izračun pa je bilo treba najprej razširiti na alikvotne dele. Vendar so bili uporabljeni in so imeli posebno oznako frakcije 2/3 in 3/4.

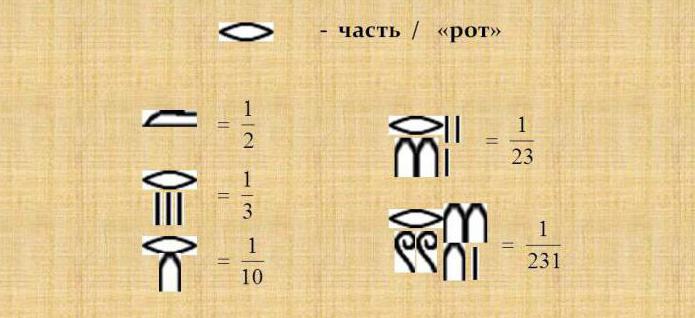
Da bi običajne frakcije prenesli v stanje alikvota na egiptovski številčni sistem, je bilo treba delati:

4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2 + 1/4 + 1/20

2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28

3/7 = 12/28 = 24/56 = 14/56 + 7/56 + 3/56 = 1/4 + 1/8 + 1/18 + 1/56.

Frakcije so bile oblikovane na sodoben način: z zmanjševanjem na skupni imenovalec so bile za številne vrednote številne pripravljene mize.

Množenje

Egipčani so se naučili želenega rezultata, ne da bi poznali tabelo množenja, vendar so uporabili znanje, da če se en faktor podvoji in drugi faktor zmanjša, se rezultat ne bo spremenil:

32 x 13 = 16 x 26 = 8 x 52 = 4 x 104 = 2 x 208 = 1 x 416

Zanimivo je, da je bila ta metoda razmnoževanja znana v Rusiji, in verjel je, da je prišla iz starega Egipta, v Evropi pa se je imenovala ruska.

Papyrus Golenishcheva

Zahvaljujoč prizadevanjem znanstvenika egiptologa V. S. Golenischeva, papirus je shranjen v Moskvi še 200 let starejši od papirusa pisarja Ahmesa. Znanstvenik ga je kupil med svojim delom v Tebi.

Napisano je bilo hieratično, v poševnem tisku, obravnava 25 problemov, podan je njihov opis po egiptovskem številčnem sistemu in rešitev. Njegova dolžina je več kot 5 m, širina 7 cm, na te probleme pa ni nobenih pripomb, kot v prejšnjem papirusu, obstajajo samo matematični izračuni.

Iz tega je razvidno, da so Egipčani z natančnostjo lahko izračunali območja trikotnika, trapeza, pravokotnika, kroga, kot tudi volumne piramide, prizme, paralelepipeda, valja in okrnjene piramide, številne formule pa popolnoma sovpadajo s sodobnimi.

V egiptovskem številskem sistemu je bilo število pi 3,16, kar je skoraj ustrezalo sodobni vrednosti 3,14, čeprav je bila takrat vrednost 3 uporabljena povsod na vzhodu.

Vse stvari so številke

Domneva se, da je Pitagora živel v Egiptu že 22 let, globoko preučuje geometrijo, filozofijo, mističnost številk. Tista odkritja, ki jih je kasneje naredila pitagorejska šola, so se lahko zgodila že v starem Egiptu.

Zato se verjame, da dela Pitagore o misticizmu številk, ki jih je kasneje napisal, temeljijo na tajnem znanju, ki ga je prejel od egiptovskih duhovnikov. Tujcev niso vzeli za študij, temveč je prišel do njih z visokim pokroviteljstvom, po pogovoru z glavnim duhovnikom, ki je bilo vredno, da je seznanjen s skrivnostmi.

Številke so bile žive osebe, ki odražajo lastnosti prostora, glasbe, energije. Vse se lahko izrazi preko matematike, opisuje vidne pojave z formulami, napoveduje nevidno, temelji na logiki in matematičnih zakonih.

Višina, širina podnožja, kot nagiba piramide Cheops v Egiptu se ujemajo z matematičnim pravilom za gradnjo pitagorejske piramide, ki prav tako potrjuje medsebojno povezanost odkritij, ki jih je ustvaril, in znanje, ki so ga pridobili stari egipčanski duhovniki, ki so uporabljali egiptovski številčni sistem.

Delo s številkami, stari misleci niso le razumeli bistva stvari, ampak so lahko vplivali tudi nanje.

Preučevanje matematike starodavnega Egipta, z uporabo egiptovskega številskega sistema, lahko samo občuduje, koliko ljudi so odkrili tisoči let pred našo dobo.