Pravokotni trapez: vse formule in primeri nalog
Naloge s trapezom se ne zdijo težke v številnih številkah, ki so bile preučene prej. Kot poseben primer se upošteva pravokoten trapez. In ko iščemo njeno območje, je včasih bolj priročno, da ga razdelimo na dva že znana: pravokotnik in trikotnik. Treba je le malo pomisliti in obstaja rešitev.
Opredelitev pravokotnega trapeza in njegovih lastnosti
Pri poljubnem trapezu so osnove vzporedne, stranice pa lahko imajo poljubno vrednost kotov. Če upoštevamo pravokoten trapez, je v njem ena od strani vedno pravokotna na osnove. To pomeni, da bosta oba vogala v njej enaka 90 stopinjam. Poleg tega vedno pripadajo sosednjim vozliščem ali, z drugimi besedami, eni strani.
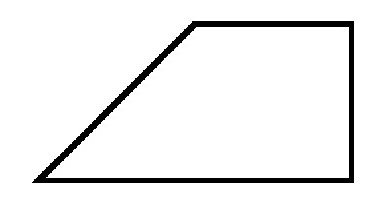
Drugi koti v pravokotnem trapezu so vedno ostri in nejasni. Njihova vsota bo vedno enaka 180 stopinj.
Vsaka diagonala se oblikuje s svojo manjšo stranjo pravokotni trikotnik. In višina, ki je potegnjena z vrha z nejasnim kotom, deli sliko na dva dela. Eden je pravokotnik, drugi je pravokoten trikotnik. Mimogrede, ta stran je vedno enaka višini trapeza.
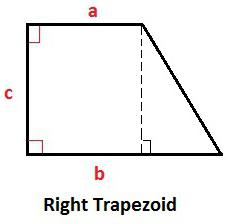
Katere oznake so sprejete v predstavljenih formulah?
Vse vrednosti, ki se uporabljajo v različnih izrazih, ki opisujejo trapez, so takoj označene in predstavljene v tabeli:
| Magnituda | Njegovo ime |
| a | večja baza |
| b | manjša osnova pravokotnega trapeza |
| c, h | pravokotno na osnovno stran, višino |
| d | nagnjena stran |
| α | akutni kot |
| β | temen kot |
| m | trapezna srednja črta |
| d 1 | manjša diagonala |
| d 2 | velika diagonala |
Formule, ki opisujejo elemente pravokotnega trapeza
Najenostavnejši od njih se nanašajo na višino in manjšo stran:
c = h.
Nekaj formul za to stran pravokotnega trapeza:
c = d * sinα;
c = (a - b) * tg α;
c = √ (d2 - (a - b) 2 ).
Prvi sledi iz pravokotnega trikotnika. In pravi, da noga do hipotenuze daje sinus nasprotnega kota.
V istem trikotniku je druga noga enaka razliki dveh baz. Zato je trditev, ki izenačuje tangens kota z razmerjem nog, resnična.
Iz istega trikotnika lahko dobimo formulo, ki temelji na poznavanju Pitagorejevega izreka. To je tretji posneti izraz.
Formule za drugo stran lahko napišemo. Prav tako so tri:
d = (a - b) / cosα;
d = c / sin α;
d = √ (c 2 + (a - b) 2 ).
Prva dva sta ponovno pridobljena iz razmerja v istem pravokotnem trikotniku, drugo pa iz Pitagorovega izreka.
Katero formulo lahko uporabimo za izračun površine?
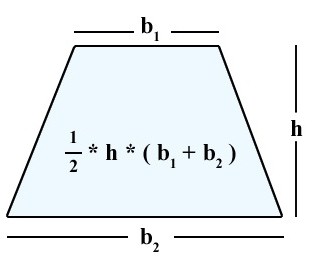
To, kar je dano za poljuben trapez. Upoštevati je treba le, da je višina stran pravokotna na podstavke.
S = (a + b) * h / 2.
Te vrednosti niso vedno podane izrecno. Da bi izračunali površino pravokotnega trapeza, morate izvesti nekaj matematičnih izračunov.
Kaj, če morate izračunati diagonalo?
V tem primeru morate videti, da tvorijo dva pravokotna trikotnika. Zato lahko vedno uporabite Pitagorov izrek. Potem bo prva diagonala izražena kot:
d1 = √ (c 2 + b 2 )
ali na drug način, ki nadomešča »od« s »h«:
d1 = √ (h 2 + b 2 ).
Podobno dobimo formule za drugo diagonalo:
d2 = √ (c 2 + b 2 ) ali d 2 = √ (h 2 + a 2 ).
Problem številka 1
Stanje Območje pravokotnega trapeza je znano in znaša 120 dm 2 . Njegova višina je dolga 8 dm. Treba je izračunati vse strani trapeza. Dodatni pogoj je, da je ena osnova manjša od druge za 6 dm.
Odločitev. Ker je podan pravokoten trapez, v katerem je znana višina, lahko takoj rečemo, da je ena stran enaka 8 dm, torej manjša stran.
Zdaj lahko preštejemo drugo: d = √ (z 2 + (a - b) 2 ). In tu sta tako stranski kot razlika med bazami takoj podani. Slednji je 6 dm, kar je znano iz stanja. Potem bo d enak kvadratni koren iz (64 + 36), to je od 100. Tako smo našli drugo stran, enako 10 dm.
Vsota osnov je mogoče najti iz formule za območje. Enaka bo dvakratni vrednosti območja, deljenega z višino. Če računate, se izkaže 240/8, zato je vsota baz 30 dm. Po drugi strani pa je njihova razlika 6 dm. Če združimo te enačbe, lahko računamo obeh osnov:
a + b = 30 in a - b = 6.
Lahko izrazite kot as (b + 6), ga nadomestite v prvi enakosti. Potem se izkaže, da bo 2b enak 24. Zato bo samo b 12 dm.
Potem je zadnja stran a enaka 18 dm.
Odgovor je. Strani pravokotnega trapeza: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.
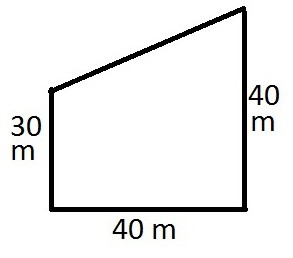
Problem številka 2
Stanje Glede na pravokotni trapez. Njegova velika stran je enaka vsoti baz. Njena višina je dolga 12 cm, zgrajen je pravokotnik, katerega stranice so enake podnožju trapeza. Potrebno je izračunati površino tega pravokotnika.
Odločitev. Začeti morate z želenim. Zahtevana površina se določi kot zmnožek a in b. Obe količini nista znani.
Potrebno bo uporabiti dodatne enakovrednosti. Ena od njih temelji na izjavi iz pogoja: d = a + b. Za to stran je treba uporabiti tretjo formulo, ki je navedena zgoraj. Izkazalo se je: d 2 = c 2 + (a - b) 2 ali (a + b) 2 = c 2 + (a - b) 2 .
Potrebno je narediti preoblikovanje, ki namesto njegove vrednosti nadomesti vrednost - 12. Po odpiranju oklepajev in postavljanju takšnih izrazov se izkaže, da je 144 = 4 ab.
Na začetku odločitve je bilo rečeno, da a * b daje zahtevano območje. Zato lahko v zadnjem izrazu ta izdelek zamenjate s S. Enostavno izračunavanje bo dalo vrednost območja. S = 36 cm2.
Odgovor je. Potrebna površina je 36 cm 2 .
Problem številka 3
Stanje Površina pravokotnega trapeza 150id3 cm². Ostri kot je 60 stopinj. Kot med majhno osnovo in manjšo diagonalo ima isto vrednost. Potrebno je izračunati manjšo diagonalo.
Odločitev. Iz lastnosti trapezoidnih kotov se izkaže, da je njegov nejasen kot 120º. Potem ga diagonala deli na enako, ker je en del že 60 stopinj. Potem je kot med to diagonalo in drugo bazo prav tako 60 stopinj. To pomeni, da je trikotnik, ki ga tvori velika podlaga, nagnjena stran in manjša diagonala, enakostranični. Tako bo želena diagonala enaka a, kakor tudi stran d = a.
Zdaj moramo razmisliti o pravem trikotniku. V njem je tretji kot 30 stopinj. Noga, ki leži proti njej, je enaka polovici hipotenuze. To pomeni, da je manjša osnova trapeza enaka polovici želene diagonale: b = a / 2. Iz nje je treba najti višino, ki je enaka strani, pravokotno na osnove. Stran s tem je noga. Iz Pitagorejevega izreka:
c = (a / 2) * √3.
Zdaj je ostalo samo, da nadomestimo vse vrednosti v formulo za območje:
150√3 = (a + a / 2) * (a / 2 * )3) / 2.
Reševanje te enačbe daje koren 20
Odgovor je. Manjša diagonala je dolga 20 cm.