Obdobje nihanja: poskusi, formule, naloge

Kakšno je obdobje nihanja? Kakšna je ta vrednost, kakšen fizični smisel ima in kako jo izračunati? V tem članku bomo obravnavali ta vprašanja, razmislili o različnih formulah, s katerimi lahko izračunamo obdobje nihanja, in ugotovili, kakšno razmerje obstaja med takšnimi fizičnimi veličinami kot čas in frekvenco nihanja telesa / sistema.

Definicija in fizični pomen

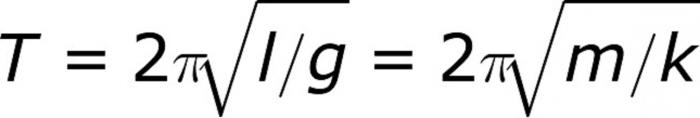
Obdobje nihanja se imenuje obdobje, v katerem telo ali sistem opravi eno nihanje (nujno popolno). Vzporedno lahko opazimo parameter, pri katerem se nihanje šteje za popolno. Vloga takega pogoja je vračanje telesa v prvotno stanje (v izvirno koordinato). Zelo dobra analogija z obdobjem delovanja. Mimogrede, napaka je misliti, da se odvija izključno v navadni in višji matematiki. Kot veste, sta ti dve znanosti neločljivo povezani. Obdobje funkcij se lahko srečuje ne samo pri reševanju trigonometričnih enačb, ampak tudi v različnih odseki fizike, gre namreč za mehaniko, optiko in druge. Pri prenosu obdobja nihanja iz matematike v fiziko je treba razumeti samo fizično količino (in ne funkcijo), ki je neposredno odvisna od časa prehoda.

Kakšna so nihanja?

Nihanja so razdeljena na harmonične in anharmonične ter periodične in neperiodične. Logično bi bilo domnevati, da se v primeru harmoničnih nihanj izvajajo v skladu z neko harmonično funkcijo. Lahko je sinus in kosinus. V tem primeru lahko pride do raztezanja stiskanja in koeficientov povečanja-zmanjšanja. Tudi oscilacije so dušene. To pomeni, da na sistem deluje določena sila, ki postopoma »upočasni« nihanja. Hkrati se obdobje zmanjšuje, frekvenca nihanja pa se stalno povečuje. Zelo dobro dokazuje tako preprost aksiom fizičnih izkušenj z uporabo nihala. Lahko je pomladnega tipa in matematičnega tipa. Ni pomembno. Mimogrede, obdobje nihanja v takih sistemih bo določeno z različnimi formulami. Toda o tem kasneje. Zdaj dajemo primere.

Izkušnje z nihali

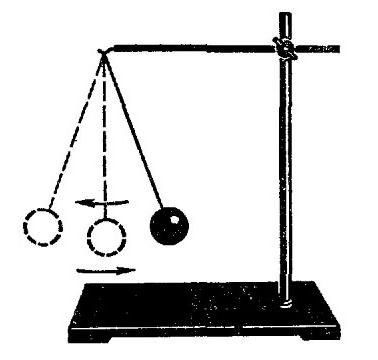
Vsako nihalo lahko vzamemo najprej, ne bo razlike. Zakoni fizike in zakoni fizike, da se v vsakem primeru spoštujejo. Ampak iz nekega razloga bolj kot matematično nihalo. Če nekdo ne ve, kaj je: to je krogla na neraztegljivi niti, ki je pritrjena na vodoravno palico, pritrjeno na noge (ali elemente, ki igrajo svojo vlogo - da sistem ohrani v ravnovesju). Kroglo je najbolje vzeti iz kovine, tako da je bila izkušnja jasnejša.

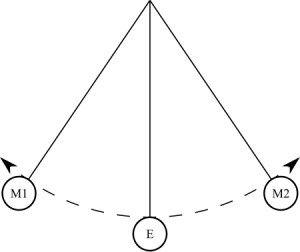
Torej, če takšen sistem izločite iz ravnotežja, uporabite nekaj sile v kroglo (z drugimi besedami, potisnite jo), potem bo žoga začela nihati na nitki, ki sledi določeni poti. Sčasoma boste opazili, da se pot, po kateri poteka žogica, zmanjšuje. Hkrati se žoga hitro premika naprej in nazaj. To kaže na to frekvenca nihanja povečuje. Vendar se čas, v katerem se žoga vrne v začetni položaj, zmanjša. Toda čas enega popolnega nihanja, kot smo ugotovili prej, se imenuje obdobje. Če se ena vrednost zmanjša, druga pa se poveča, potem govorimo o obratni sorazmernosti. Tako smo prišli do prve točke, na podlagi katere so zgrajene formule za določanje obdobja nihanja. Če vzamemo vzmetno nihalo, potem bo zakon tam opazen v nekoliko drugačni obliki. Da bi bilo to najbolj jasno predstavljeno, bomo sistem premaknili v navpični ravnini. Da bi bilo bolj jasno, je bilo sprva vredno povedati, kaj je pomladni nihalo. Iz imena je razvidno, da mora biti v njegovi zasnovi prisotna vzmet. In to je res. Ponovno imamo vodoravno ravnino na oporah, na katero je vzmetena vzmet določene dolžine in togosti. Za njo pa je suspendirana teža. Lahko je valj, kocka ali druga številka. Morda je celo izdelek tretje osebe. V vsakem primeru, ko odstranite sistem iz ravnotežnega položaja, bo začel izvajati dušene oscilacije. Najbolj jasno vidno povečanje frekvence je v navpični ravnini, brez kakršnega koli odstopanja. Pri tem lahko poskusite končati.

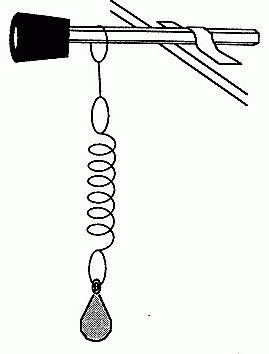
Tako smo ugotovili, da sta obdobje in frekvenca nihanja dve fizikalni velikosti, ki imata inverzno razmerje.

Označevanje količin in dimenzij

Običajno je obdobje nihanja označeno z latinično črko T. Veliko manj pogosto jo lahko označimo drugače. Pogostnost je označena s črko µ ("Mu"). Kot smo rekli na samem začetku, obdobje ni nič več kot čas, v katerem se v sistemu zgodi popolno nihanje. Potem bo dimenzija obdobja druga. In ker sta obdobje in frekvenca obratno sorazmerna, bo dimenzija frekvence deljena z drugo. V posnetkih opravil bo vse izgledalo takole: T (s), µ (1 / s).

Formula za matematično nihalo. Problem številka 1

Kot v primeru poskusov sem se najprej odločil, da se ukvarjam z matematičnim nihalom. V izpeljavo formule ne bomo šli podrobno, saj taka naloga na začetku ni bila določena. In sam zaključek je okoren. Oglejmo si tudi same formule, ugotovimo, kakšne so vrednote v njih. Tako je formula za obdobje nihanja matematičnega nihala naslednji:

Kjer je l - dolžina niti, n = 3,14 in g - pospešek prosti padec (9,8 m / s ^ 2). Formula ne sme povzročati težav. Zato brez dodatnih vprašanj nemudoma nadaljujemo z reševanjem problema določanja obdobja nihanja matematičnega nihala. Kovinska krogla, ki tehta 10 gramov, je obešena na neraztegljivo nit dolžine 20 centimetrov. Izračunajte obdobje nihanja sistema in ga vzemite kot matematično nihalo. Rešitev je zelo preprosta. Kot pri vseh fizikalnih problemih, je potrebno zaradi zavračanja nepotrebnih besed čim bolj poenostaviti. Vključeni so v kontekst, da bi zamenjali odločevalca, v resnici pa nimajo nobene teže. V večini primerov seveda. Tukaj lahko izločite trenutek z »neločljivo nitjo«. Ta stavek ne sme priti v stupor. In ker imamo matematično nihalo, nas ne sme zanimati masa tovora. To pomeni, da besede okoli 10 gramov prav tako preprosto pomenijo, da študenta zmedejo. Vemo pa, da v formuli ni mase, zato lahko s čisto vestjo odločamo. Zato vzamemo formulo in preprosto nadomestimo vrednosti v njej, ker je potrebno določiti obdobje sistema. Ker niso bili določeni dodatni pogoji, bomo zaokrožili vrednosti na tretje decimalno mesto, kot je običajno. Če pomnožimo in delimo vrednosti, ugotovimo, da je obdobje nihanja 0,886 sekund. Problem rešen.

Formula za pomladno nihalo. Problem številka 2

Formule nihalov imajo skupni del, in sicer 2p. Ta vrednost je prisotna v dveh formulah hkrati, vendar se radikalno izražata. Če se pri problemu v zvezi s časom vzmetnega nihala pokaže teža obremenitve, je nemogoče izogniti se izračunov z njeno uporabo, kot je bilo pri matematičnem nihalu. Toda ne smete se bati. Tu je formula za obdobje pomladnega nihala:

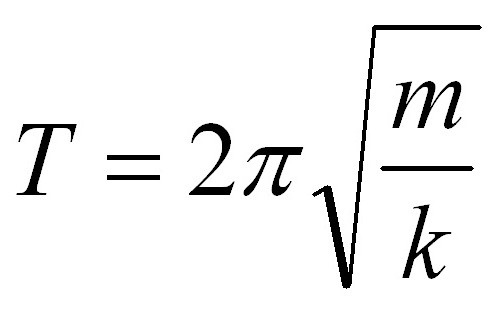
V njej je m masa obremenitve vzmeti, k je konstanta vzmeti. V nalogi je mogoče podati vrednost koeficienta. Toda, če v formuli matematičnega nihala niste še posebej jasni - navsezadnje sta 2 od 4 vrednosti konstante - dodan je 3 parameter, ki ga lahko spremenite. In na izhodu imamo 3 spremenljivke: obdobje (frekvenca) nihanj, vzmetno konstanto vzmeti, maso visečega tovora. Naloga je lahko usmerjena v iskanje katerega koli od teh parametrov. Preveč enostavno bi bilo pogledati za določen čas, zato bomo malce spremenili stanje. Poiskati koeficient togosti vzmeti, če je skupni čas nihanja 4 sekunde, teža vzmetnega nihala pa 200 gramov.

Da bi rešili vsak fizični problem, bi bilo dobro najprej narisati sliko in napisati formule. Tukaj so pol bitke. Pri pisanju formule je potrebno izraziti koeficient togosti. Imamo ga pod korenom, tako da bomo obkrožili obe strani enačbe. Če se želite znebiti frakcije, jih pomnožite s k. Sedaj pustimo le koeficient na levi strani enačbe, torej delimo dele s T ^ 2. Načeloma bi lahko bila naloga nekoliko težja, ne pa določanje obdobja v številkah, temveč pogostost. V vsakem primeru se pri izračunu in zaokroževanju (dogovorili smo se zaokrožiti na tretje decimalno mesto) izkaže, da je k = 0, 157 N / m.

Obdobje prostih nihanj. Formula časa prostih nihanj

Pod formulo za obdobje proste vibracije razumeli formule, ki smo jih razvrstili v prej omenjenih dveh problemih. Sestavljena je tudi enačba prostih nihanj, toda že govorimo o premikih in koordinatah, to vprašanje pa se nanaša na drug članek.

Nasveti za reševanje težav, povezanih z obdobjem

1) Preden se lotite naloge, zapišite formulo, ki je z njo povezana.

2) Najenostavnejše naloge ne zahtevajo slik, v izjemnih primerih pa jih je treba opraviti.

3) Poskusite se znebiti korenin in imenovalcev, če je mogoče. Enačba, napisana v vrsti, ki nima imenovalca, je veliko lažje in lažje rešiti.