Merjenje lomnega količnika stekla. Laboratorijske vaje

Poznavanje lomnega količnika določenega stekla je pomembno za njegovo uporabo kot material za optične leče. V tem članku predstavljamo laboratorijsko delo o merjenju lomnega količnika stekla, ob upoštevanju vseh potrebnih formul na poti.

Namen in cilji laboratorijskega dela

Laboratorijsko merjenje lomnega količnika stekla je namenjeno doseganju naslednjega cilja: naučiti se meriti lomne lastnosti transparentnih materialov in obdelati rezultate.

Med delom je treba rešiti naslednje naloge:

• Študij teoretičnega gradiva.
• Študija eksperimentalne postavitve in njenega načela delovanja.
• Za izračun vpadnih in lomnih kotov.
• Določite kritični kot.
• Poiščite vrednost refrakcijskega indeksa za steklo in obdelajte rezultate.
• Pripravite zaključke o delu.

Teorija fenomena refrakcije

Ta pojav sestoji iz spreminjanja smeri pravokotnega gibanja svetlobnega snopa, ko se premika iz enega transparentnega medija v drugega. Takšna situacija nastane, na primer, ko svetloba prečka mejo voda - zrak ali steklo - zrak.

Zakoni lomljenja so v svoji zgodovini zanimali človeštvo. Ukvarjali so se z antičnimi Grki (Ptolomej, I-II. Stoletje), Arabci v srednjem veku (Ibn Sahl, X. stoletje), pa tudi mnogi znanstveniki v novem času (Huygens, Newton, Descartes, Snell). Trenutno se verjame, da je Nizozemec Snell najprej oblikoval zakon loma v sodobni obliki, ki povzema veliko eksperimentalnih podatkov.

Formula za fenomen refrakcije ima naslednjo obliko:

n ₁ * sin (θ ₁ ) = n ₂ * sin (θ ₂ ) = const.

Tu je θ ₁ kot glede na normalo do vmesnika med medijem, pri katerem žarek doseže to površino, θ ₂ je kot glede na isto normo za lomljeni žarek. Vrednosti n ₁ , n ₂ so lomni indeksi medijev 1 oziroma 2. Indikator n določa, kako močno medij upočasni hitrost svetlobe glede na to v vakuumu, to je:

n = c / v, c je hitrost svetlobe v vakuumu, v je v mediju.

Kritični kot

Snellov zakon dokazuje, da je vpadni kot večji od kota loma, če je 1. medij optično manj gost (n ₁₎ 2). To je tudi obratno.

Ko se žarek premakne v optično bolj gostem mediju in preide skozi vmesnik med medijem v manj gosto prosojno snov, potem obstaja kot, pod katerim se lomljeni žarek premika vzdolž površine, ki ločuje medij. Ta kot je kritičen. Vsi vpadni koti, ki so večji od tega, bodo vodili do dejstva, da noben del svetlobe ne gre skozi vmesnik. Ta pojav se imenuje notranji popoln odsev.

Glede na zakon Snell in zgornja pojasnila lahko za kritični kot pišete:

θ ₁ = arcsin (n ₂ / n ₁ ), kjer je n ₁ > n ₂ .

Ta pojav se uporablja v optičnih vlaknih za prenos elektromagnetne energije na dolge razdalje brez izgube.

Poskusna nastavitev

Določanje lomnega količnika stekla se izvede z namestitvijo, kar je prikazano na spodnji sliki.

Številke na fotografiji pomenijo naslednje:

1. Prehodna črta, na kateri so glavne delovne naprave naprave.
2. Vir električne energije.
3. Svetilka, ki je vir svetlobe.
4. Zbirna leča z znano goriščno razdaljo (na primer 10 cm).
5. Kaseta za membrane.
6. Apertura v obliki rešetke (odprtine se uporabljajo za boljši fokus svetlobnega žarka.).
7. Optični graduirani disk.
8. Stekleni predmet, katerega lomni količnik je treba izmeriti. Ima obliko pol-cilindra, kar pomeni, da so njegove tri ploskve ravnine, četrta pa je valjasta.
9. Optična prizma (ne uporablja se za to laboratorijsko delo).

Zakaj je potrebno uporabiti stekleni predmet v obliki pol-cilindra, bomo razložili spodaj.

Priprava naprave za delovanje

Načelo delovanja naprave za eksperimentalno merjenje lomnega količnika stekla je zelo preprosto: potrebno je le tvoriti ozek svetlobni žarek, poslati ga vzporedno z optičnim diskom skozi stekleni polvaljnik in z gradacijo diska izmeriti vpadni kot in lomni kot.

Priprava za vgradnjo poteka zaporedno:

1. Vir svetlobe (luč) položite na merilno ravnilo v položaju "0 cm".
2. Postavite telo z zbiralno lečo na merilno ravnilo v položaju, ki je enak goriščni razdalji. V tem primeru 10 cm, zaradi tega položaja bodo vsi žarki, ki jih žarnica oddaja iz leče, vzporedni z merilno ravnino.
3. Vklopite vir napajanja in s prilagoditvijo položaja diafragme zagotovite, da je svetlobni snop čim bolj ozek. Njegova debelina mora biti veliko manjša od najmanjše delitve na optičnem disku.
4. Prilagodite višino položaja optičnega diska, tako da svetlobni žarek preide čez njo in se skoraj dotika njegove površine. Disk mora biti nastavljen tudi glede na stransko os, tako da žarek prehaja točno skozi njegovo središče, to je skozi enega od premerov.
5. V središču plošče položite stekleni polcilindar tako, da njegova stranska ravnina sovpada z enim od premerov plošče.

Nastavitev je pripravljena za poskus.

Izvedba poskusa

Delo laboratorija "Merjenje indeksa loma stekla" je sestavljeno iz dveh stopenj. Najprej izvedite poskus, da premaknete žarek svetlobe iz zraka v steklo in nato iz stekla v zrak:

• Od zraka do stekla. Najprej morate obrniti optični disk, tako da po prehodu skozi polvaljnik žarek ne lomi. Ta položaj bo ustrezal izvoru (0 ^o ). Po tem je potrebno zavrteti disk za vsakih 5 ^o in vnesti podatke v ustrezno tabelo: α in β - vpadne kote in lom. Potrebno je izvesti približno 10-15 meritev. Položaj pol valja na disku si lahko ogledate na spodnji sliki (a).
• Od stekla do zraka. V tem primeru je treba disk s polcilindrom zasukati za 180 ^o . V tem primeru bo vpadni žarek najprej padel na valjasto površino. Ker pade na njem vzdolž polmera (pod kotom 90 ^o ), ne pride do refrakcije na vhodu v steklo in se pojavi le na izhodu iz nje skozi ravno površino. To stanje je prikazano na spodnji sliki (b). Če izberete referenčno točko kot v zgornjem primeru, zavrtite disk vsakih 5 ^o in izmerite kot.

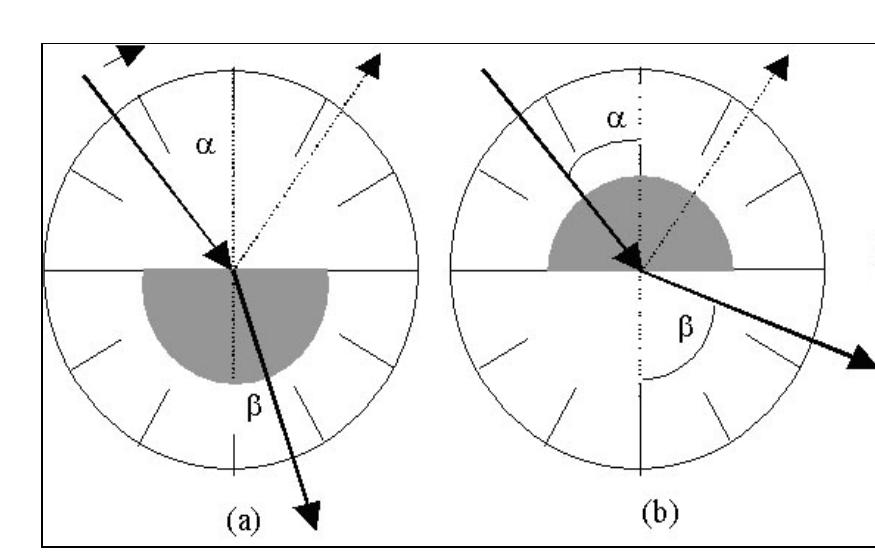
Ko se izvede poskus »steklo-zrak«, nastane situacija pri določenem vpadnem kotu žarka, ko ne pride ven skozi ravno površino pol-cilindra. Ta kot je kritičen.

Rezultati obdelave

Za vsak par kotov α in β izračunamo vrednost n _i za steklo. To naredimo s pomočjo formul za merjenje indeksa lomov stekla. Rešitev iz Snellovega zakona je naslednja:

• Od zraka do stekla: n _i = n _v * sin (α) / sin (β).
• Od stekla do zraka: n _i = n _v * sin (β) / sin (α).

Refrakcijski indeks zraka je enak n _v = 1.00029.

Tako dobimo niz vrednosti n (njihovo število je enako skupnemu številu opravljenih meritev). Naj bo to število m. Sedaj je treba najti povprečno vrednost za lomni količnik stekla n¯, kot tudi varianco Δn (srednji kvadratni odklon), ki kaže točnost poskusa. Te vrednosti so določene z naslednjimi formulami:

np = ∑ _{i = 1} ^m (n _i ) / m;

Δn = √ ( _{= i = 1} ^m (n _i -n¯) ² / m).

Končni rezultat je zapisan v obliki:

np ± Δn.

Zaključki laboratorijskega dela

Po opravljenem delu "Merjenje lomnega količnika stekla" lahko sklepamo naslednje:

• žarek svetlobe se lomi po prehodu v drug medij;
• kritični kot nastane le v primeru prehoda svetlobe iz stekla v zrak, vendar ne obratno;
• zaradi zanesljivosti dobljenih rezultatov je treba izvesti več meritev (več kot 10), nato pa je treba končno vrednost predstaviti kot povprečno vrednost, ki kaže mejo njene točnosti.