Klein steklenica: lastnosti in uporaba

Kleinova steklenica je dvodimenzionalna zbirka, določena neusmerljiva površina. Prvič ga je leta 1882 opisal nemški matematik Klein. Če razrežete Kleinovo steklenico vzdolž njene osi simetrije na polovico na enake dele, bo rezultat Mobiusov trak. Samo ime, najverjetneje, izhaja iz napačnega prevoda iz nemške besede Flache - površina. Z besedo je beseda blizu besede Flasche - steklenica. V prihodnosti se je to ime v tej različici vrnilo v nemški jezik.

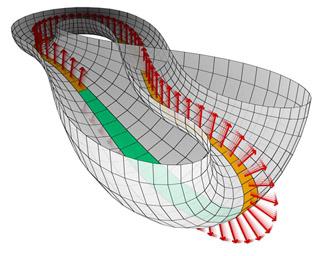
Krogla od znotraj navzven

Mobius Tape, Kleinova steklenica in heptaedar - vse to je popolna statična oblika z notranjimi površinami. V 20. stoletju so topologi začeli reševati probleme dinamične narave, prva izmed njih pa je bila inverzija krogle. Za razliko od zgornjih številk je površina krogle usmerjena. Njegova notranja stran je lahko obarvana modro, zunanja - v rdeči barvi. Če po takšnem obarvanju površin na nekem mestu spreminjamo južni in severni pol krogle, ju premikamo po povezovalni osi, se krogla obrne navzven tako, da njena zunanja površina postane modra, notranja površina pa postane rdeča. Na celotnem obodu ekvatorja se oblikuje pregib. Ampak to še ni vse: ko poli preidejo vzdolž osi večino poti in zunanja površina krogle spremeni barvo iz rdeče v modro, potem dolžina ekvatorja izdelali bomo toroidno površino, ki bo od zunaj pobarvana rdeče. Zato je krogla, prikazana na pol, pokazala še en zanimiv učinek v topologiji - prepletanje zunanjega in notranjega prostora, saj obe površini izstopata od zunaj.

Kako zgraditi model steklenice Klein

Najprej morate vzeti steklenico z luknjami v steni in na dnu ter potegniti vrat, jo upogniti in skozi luknjo v steni. Če v štiridimenzionalnem prostoru zgradite model prave steklenice, potem v steni ni potrebe po luknji. Toda brez tega ni mogoče, če je model zgrajen v tridimenzionalnem evklidskem prostoru (R3). Nato je treba na luknjo na dnu pritrditi vrat. Kleinova steklenica, za razliko od običajnega stekla, nima »roba«, kjer se površina nenadoma konča. Če jo primerjamo z balonom, potem pot od znotraj navzven prehaja, ne da bi prečkala površino. Torej v resnici objekt nima niti notranje niti zunanje površine.

Klein steklenica: uporaba in lastnosti

Ta objekt, tako kot Mobiusov trak, je dvodimenzionalni diferenciabilni ne-orientabilni kolektor. Ampak, za razliko od traku, je Kleinova steklenica kompaktna zbirka brez roba. Če na robovih zlepimo dve robovi Mobiusa, dobimo steklenico Kleina. To pa ni mogoče storiti v običajnem prostoru (R3), ne da bi ustvarili samo-presečišče. Steklenico Klein lahko potopite le v vodo tridimenzionalni prostor hkrati pa se lahko vključi v štiridimenzionalni prostor. Ta objekt ima kromatično število površin šestih.