Poiščite koren enačbe? To je enostavno!
V matematiki obstajajo različne enačbe. Vedno jih je treba rešiti, tj. Poiskati vse številke, ki bodo resnično enakopravne. Načini iskanja rešitev so določeni z izvirno obliko enačbe. Od njega bo odvisno število dejanskih vrednosti spremenljivke, ki so označene kot koren enačbe. To število se lahko spreminja od nič do neskončnosti.
Kaj pomeni enačba in njen koren?
Iz naslova je jasno, da izenačita dve vrednosti, ki jih lahko predstavimo z numeričnimi ali abecednimi izrazi. Poleg tega vsebujejo še neznane količine. Najenostavnejša enačba ima samo eno.
Obstaja veliko število enačb, vendar je koncept korena zanje vedno enak. Koren enačbe je taka vrednost neznanega števila, pri katerem enačba prevzame pravo enakost. Obstajajo situacije, ko je takih števil več, potem se neznano imenuje spremenljivka.
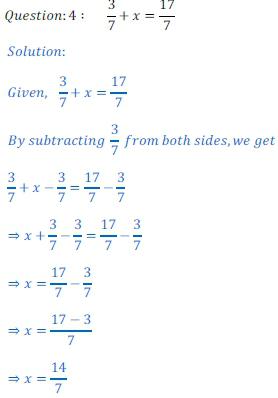
Iskanje vseh možnih korenin enačbe je njena rešitev. To pomeni, da morate izvesti vrsto matematičnih operacij, ki jo poenostavijo. Potem pa vodi k enakosti, ki vsebuje samo neznano in številčno.
V algebri lahko pri reševanju enačb pride do situacije, da korenin sploh ne bo. Potem pravijo, da je netopna. In v odgovoru take enačbe je potrebno zapisati, da ni rešitve.
Ampak včasih se zgodi nasprotno. To pomeni, da se v procesu številnih transformacij pojavijo tuje korenine. Pri zamenjavi ne bodo zagotovili resnične enakosti. Zato je treba številke vedno preveriti, da se izognemo situaciji z nepotrebnimi koreninami v odgovoru. V nasprotnem primeru se enačba ne bo štela za rešeno.
O linearni enačbi
Vedno se lahko pretvori v zapis naslednje oblike: a * x + v = 0. V njej je “a” vedno ne-nič. Da bi razumeli, koliko korenov ima enačba, jo bo treba rešiti v splošni obliki.
Algoritemske spremembe:
- premaknemo izraz »v« na desno stran enakosti in zamenjamo njegov znak z nasprotnim;
- na obeh straneh nastale enakosti delimo s koeficientom a.
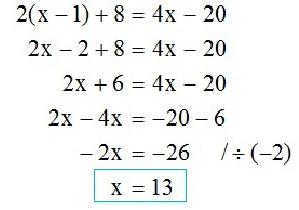
Splošni pogled na rešitev je:
x = -in / a .
Iz tega je jasno, da je odgovor ena številka. To je samo en koren.
Kvadratna enačba
Njegova splošna oblika: a * x 2 + b * x + c = 0 . Tu so koeficienti poljubne številke, razen prvega, "a", ki ne more biti enaka nič. Navsezadnje bo samodejno postal linearen. Odgovor na vprašanje, koliko korenov ima enačba, ni več tako enostavna kot v prejšnjem primeru.
Vse bo odvisno od vrednosti diskriminanta. Izračuna se po formuli D = v 2 - 4 a * s . Po izračunih se lahko »D« izkaže za več, manj ali enako nič. V prvem primeru bodo korenine enačbe dve, v drugem pa bo odgovor »brez korenin«, tretji pa samo eno neznano vrednost.
Formule, ki se uporabljajo za iskanje korenin kvadratne enačbe in vsebujejo diskriminantno
V splošnem primeru, ko je "D" pozitivno število, ki ni enako nič, morate uporabiti naslednjo formulo:
x 1,2 = (-v ± √D) / (2 * a) .
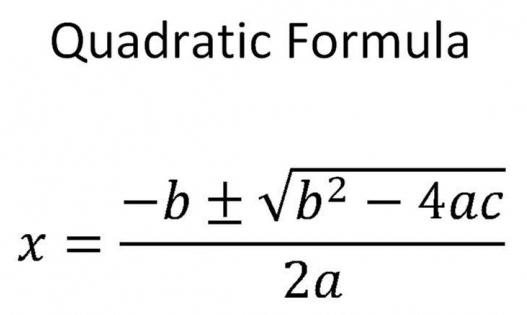
Tukaj sta vedno dva odgovora. To je posledica dejstva, da je izvirna formula plus / minus. To bistveno spremeni vrednost neznanega.
Ko je "D" enaka nič, je koren enačbe edina številka. Samo zato kvadratni koren od nič je nič. Torej, dodati in odštevati bo treba nič. Iz te številke se ne bo spremenilo. Zato lahko formulo korena enačbe zapišemo brez omembe "D":
x = (-v) / (2 * a).
Če je diskriminanten negativen, iz njega ni mogoče izvleči kvadratnega korena. Zato korenine takšne enačbe ne bodo.
Opomba To velja za šolski tečaj, ki se ne poučuje. kompleksnih števil. Ko vstopijo, se izkaže, da bodo v tem primeru dva odgovora.
Formule za izračun korenov kvadratne enačbe, ki ne uporabljajo diskriminantne
Govorimo o izreku Vieta. To velja v primeru, ko je kvadratna enačba napisana v nekoliko drugačni obliki:
x 2 + c * x + c = 0.
Potem korensko formulo kvadratna enačba gre za izpolnitev rešitve dveh linearnih:
x 1 + x 2 = -in
in
x 1 * x 2 = s.
Rešeno je zaradi dejstva, da je izraz za enega od korenin izpeljan iz prvega. To vrednost je treba nadomestiti z drugo. Torej bo najti drugi koren, nato pa prvi.
Ta možnost lahko vedno izhaja iz splošne oblike kvadratne enačbe.
Dovolj je, da vse koeficiente razdelimo na "a".
Kaj, če morate vedeti najmanjšo vrednost korena?
Rešite enačbo in poiščite vse možne številke, ki so primerne za odgovor. In potem izberite najmanjšo. To bo najmanjši koren enačbe.
Najpogosteje se taka vprašanja nahajajo v nalogah, ki imajo stopnjo, večjo od 2, ali vsebujejo trigonometrične funkcije. Primer, ko morate najti najmanjši koren, je naslednja enakost:
2 x 5 + 2 x 4 - 3 x 3 - 3 x 2 + x + 1 = 0.
Da bi našli vsako vrednost, ki jo lahko imenujemo "koren enačbe", je treba to enačbo preoblikovati. Prvo dejanje: združiti člane v parih: prvo z drugim in tako naprej. Nato iz vsakega para naredite skupen dejavnik.
V vsakem oklepaju ostane (x + 1). Skupni faktor v prvem paru bo 2 x 4 , v drugem pa 3 x 2 . Zdaj morate ponovno uvesti skupni dejavnik, ki bo enak ogrodju.
Po množilniku (x + 1) bo (2 x 4 - 3 x 2 + 1). Produkt dveh faktorjev je enak nič, samo če eden od njih vzame vrednost, ki je enaka nič.
Prva oklepaja je nič za x = -1. To bo eden od korenin enačbe.
Drugi bodo pridobljeni iz enačbe, ki jo oblikuje drugi oklep, enačena z ničlo. Je dvakratni. Da bi jo rešili, morate vnesti zapis: x 2 = y. Nato se bo enačba bistveno spremenila in vzela običajno obliko kvadratne enačbe.
Njegova diskriminantna je D = 1. Je večja od nič, kar pomeni, da bosta dve koreni. Prvi koren je enak 1, drugi pa 0,5. Ampak to so vrednosti za y.
Vrniti se morate na vneseno oznako. x 1.2 = ± 1, x 3.4 = ± √0.5. Vsi koreni enačbe: -1; 1; -0,5; .0.5. Najmanjša med njimi je -1. To je odgovor.
Kot zaključek
Opomnik: vse enačbe je treba preveriti, ali je koren ustrezen. Mogoče je tujec? Treba je preveriti predlagani primer.
Če nadomestimo enoto v prvotno podani enačbi namesto "x", se izkaže, da je 0 = 0. Ta koren je pravilen.
Če je x = -1, je rezultat enak. Primerna je tudi korenina.
Podobno se z vrednostmi "x", ki so enake -0,5 in .50,5, ponovno pokaže prava enakost. Vse korenine se prilegajo.
Ta primer ni prinesel tujih korenin. To ni vedno tako. Lahko je tudi to, da najmanjša vrednost ne bi bila primerna za testiranje. Potem bi moral izbrati med ostalimi.
Zaključek: treba se je spomniti na pregled in skrbno pristopiti k rešitvi.