Primer algoritma Diffieja Hellmana

Razkritje teme kriptografije javnega ključa se mora začeti z zgodovinsko potjo problema. Whitfield Diffie in Martin Hellman sta prva vprašala o odprti metodi predaje ključev. To se je zgodilo leta 1976. Publikacija je prvič poskušala rešiti problem. Njihova rešitev ni bila brez pomanjkljivosti, ampak je postavila temelje za popolnoma drugačen način razmišljanja na področju šifriranega prenosa podatkov.

Predpogoji za izdelavo Diffie-Hellmanovega algoritma

Do tega trenutka sta bila avtentifikacija in šifriranje mogoča le prek skupnega tajnega ključa. Z razvojem tehnologije je vprašanje postalo vse bolj pereče. Če mora 10 ljudi med seboj prenesti podatke prek nezanesljivih kanalov, bodo morali med seboj izmenjati gesla. Ta naloga izgleda resnično. Tudi če jih je treba posodobiti. Konec koncev boste za 10 prijateljev potrebovali le 45 tajnih ključev. In če bodo stiki 100? To bo trajalo 4950 gesel. Položaj narašča kot snežne kepe.

Glavni dosežek Diffija in Hellmana je bila pravilna formulacija vprašanja in iznajdljiv odgovor na to vprašanje. Predlagali so, da se podatki lahko šifrirajo na en način in dešifrirajo v drugi. To pomeni, da imata 2 ključa. Tisto, ki se uporablja za šifriranje, lahko pustite odprto. Tako lahko vsaka oseba šifrira sporočilo, vendar ga lahko dešifrirajo samo lastniki drugega tajnega ključa. Ampak kako izvajati algoritem za prenos takega ključa? Znanstveniki so lahko delno odgovorili.

Kratka matematika: skupine

Diffie-Hellmanov algoritem ali protokol (nadaljnji DH) deluje s pomočjo enostavnih števil. Naj bo dovolj veliko število, ki pripada setu številke. Algoritem vključuje uporabo številnih 250-500 bajtov. Naj je Za multiplikativna skupina obročka za ostanke modulo a, ki ga bo uporabil Diffie-Hellmanov algoritem za šifriranje. Sestavljen je iz niza števil 1, ..., a-1.

Vzemite nekaj elementa b iz skupine Z _a in razmislite o neskončnem zaporedju 1, b, b ² , b ³ , b ⁴ , ... Iz dejstva, da je skupina Z _a po definiciji končni niz, prej ali slej upoštevano zaporedje {b} se bo ponovilo. Nastavite b ⁱ = b ^j (i <j).

Zdaj delimo vsak del enakosti z b ⁱ (modulo a) in dobimo b ^ji = 1. To pomeni, da je število k = ji, za katerega je b ^k = 1 (mod a) resnično. Najmanjši k, za katerega velja ta enakost, se imenuje vrstni red b. Da bi se izognili zamenjavi z drugo posebno literaturo, se za razlago sistema Diffie-Hellman uporablja standardna matematična notacija.

Tako dvig števila b, imenovanega generirni element, na moč dobimo zaporedje števil (množice) 1, ..., b ^k-1 . Število elementov v tem nizu je točno k.

Lastnost množenja po modulu a pravi, da obstaja vsaj ena številka b, ki generira vse elemente skupine Z * _a . Z drugimi besedami, obstaja število, za katerega velja k = a - 1. Ta lastnost nam omogoča, da predstavimo številke skupine Z * _a v obliki 1, b, b ² , ... b ^a-2 . Takšno število b se imenuje primitivno število skupine.

V nadaljevanju je iz skupinskih znakov enostavno dokazati, da je množica, ki jo generira številka b, tudi sama skupina in podeduje vse lastnosti skupin. Z drugimi besedami, operacije znotraj ustvarjene skupine ali podskupine se lahko izvedejo na popolnoma enak način kot v skupini modulo a.

Razmislite o izjavi. Za vsak element b njegov red je delitelj a-1. To je enostavno pokazati. Naj bo a = 7. Število b = 3 je primitivno, saj 1, ..., b ⁵ = 1, 3, 2, 6, 4, 5. Nato bo število h = 2 ustvarilo podskupino 1, ..., h ² = 1 , 2, 4, ker h ³ = 2 ³ mod 7 = 1. h = 6 ustvarja podskupino 1, 6. Velikosti skupin so 3 oziroma 2. Očitno so delitelji števila a-1 = 6.

Prvi DH algoritem

V prvotni različici je algoritem delal na naslednji način. Veliko število a je izbrano iz množice enostavnega in primitivnega elementa b, ki generira Z * _a . Obe številki a in b predstavljata javni ključ, ki ju poznajo vsi, vključno z napadalci. Kako potem skriti sporočila?

Na tem koraku sta Diffie in Hellman prišla do zelo domiselne poteze. Recimo, da imamo dve osebi, ki komunicirata drug z drugim: A in B. Najprej A izbere naključno število x od Z * _a , kar je enako izbiri števila iz {1, ..., a-1}. Nato izračuna vrednost s formulo (b ^x mod a) in jo pošlje na B. Po drugi strani pa B izbere določeno število y iz istega niza, izračuna vrednost (b ^y mod a) in pošlje rezultat nazaj na A.

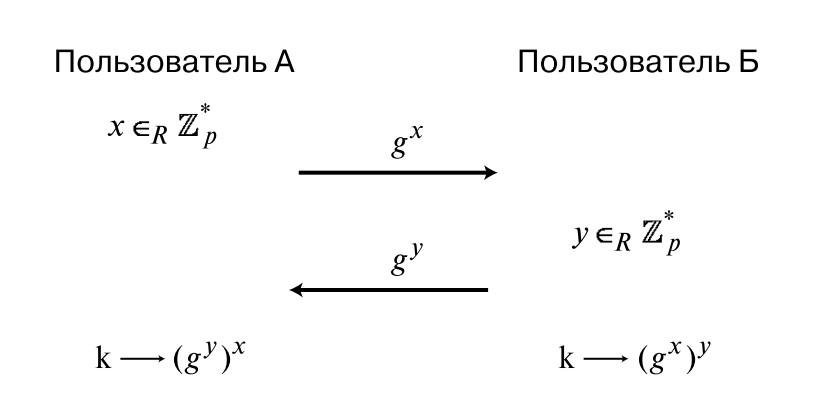
Na tako zapleten način se izkaže, da skrivni ključ izgleda kot b ^xy . Zaradi lastnosti stopinj, ki pravijo g ^xy = (g ^y ) ^x , lahko sogovornik A izračuna želeno vrednost in dešifrira informacije, ki so mu poslane. Na enak način izračuna sogovornik B. Tako imata oba isti tajni ključ.

Kakšne težave ima vsiljivec s to izmenjavo informacij? Lahko prestreže številke g ^x in g ^y . Tudi s poznavanjem javnih ključev problem izračuna g ^xy ni trivialen, t. Ker ni učinkovitega algoritma za iskanje želene vrednosti v distribuciji Diffie-Hellmanovih ključev. Ta problem je znan kot problem izračunavanja diskretnega logaritma.

Mediatorski napad

Ena od slabosti primarnega Diffie-Hellmanovega algoritma je njegova ranljivost pred posredniškimi napadi. Kaj to pomeni? Sogovornik A ve, da komunicira z določenim obrazom, vendar še posebej s kom - nima pojma. Tako lahko napadalec prodre v prenos informacij in posnema sogovornika B, ko komunicira z A, in obratno. Nihče od njih ne bo mogel sumiti, da je nekaj narobe.

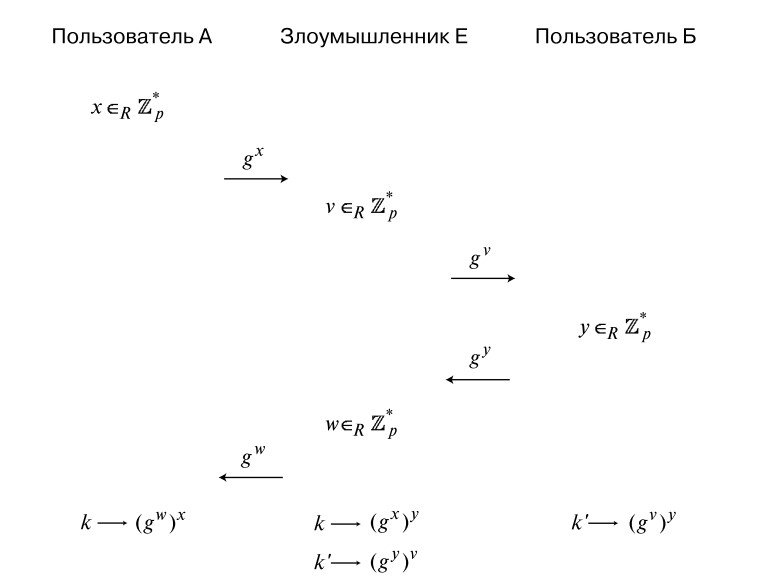
Obstaja samo eno področje uporabe, v katerem so napadi na Diffie-Hellmanov algoritem izključeni. To je telefonski in video klic. Tukaj se sogovorniki lahko spoznajo, tako da posrednik ne bo mogel prodreti.

Pasti

Poleg posredniškega napada protokol DH skriva še vrsto drugih težav. Na primer, ena od pomanjkljivosti je primer, ko primitiv ni primitivna. Potem ustvari samo podskupino. Zaradi zmanjšanja števila možnih možnosti se lahko napadalcu dovoli iskanje

Težavam zaradi te pomanjkljivosti se je mogoče izogniti, če vsak sogovornik pred začetkom izmenjave podatkov preveri pravilnost številk a in b. To pomeni, da je a praštevilo in b primitivno. Vendar pa, ko gre za varnost z izvajanjem nekaterih enotnih, neobveznih korakov, jih uporabniki pogosto ignorirajo.

Drug resen problem nastane na podlagi podskupin po modulu a. Če se napadalec odloči spremeniti g ^x na 1, da bi mu olajšal prisluškovanje, ga lahko uporabniki zlahka zaznajo s preverjanjem številke za tekmo. Če pa zamenja ključ z nizko številko naročila, uporabniki ne bodo mogli ničesar domnevati. In ker bo število elementov v nizu z nizkim naročilom majhno, bo napadalec moral rešiti majhno število možnosti za dekodiranje.

Zanesljivost praštevil

DH algoritem uporablja veliko in zanesljivo število številnih preprostih. Kako točno izbrati? Analiziramo korake.

1. S formulo a = 2k + 1 izberemo številke a in k tako, da sta preprosta.
2. Iz množice 1, ..., a-1 izključimo 1 in a-1.
3. Iz niza, ki ostane po drugem koraku, vzamemo naključno število x in poiščemo vrednost b = x ² (mod a).
4. Prepričajte se, da b ni enak 1 ali a-1. Če je b enaka eni od prepovedanih vrednosti, izberite drugo x. In ponovite operacijo.

Tako dobljeni niz (a, k, b) se lahko šteje za zadostnega za uporabo v algoritmu za izmenjavo ključev Diffie-Hellman. V skladu s tem mora prejemnik sporočila preveriti tudi vrednost, ki mora biti moč b, in se prepričati (npr. O funkciji simbola Legendre), da pade v niz, ki ga generira številka b.

Uporaba podskupin

Glavna pomanjkljivost zgoraj navedenega algoritma je nezadostna učinkovitost. Če predpostavimo, da je dolžina praštevila a n bitov, potem je k n-1 bitov. Izkazalo se je, da bo vsaka stopnja dolga n-1. Nato operacijo izpostavljenosti v povprečju bo sestavljen iz 3n / 2 množenja mod a. To je velik proces.

Da bi se soočili s tem problemom, smo se odločili za uporabo manjših podskupin. Kakšen je dobiček v tem primeru? Če je število a sestavljeno iz 2000 bitov, je za izračun b ^x potrebno 3000 operacij množenja. Z uporabo podskupin se lahko to število zmanjša na ~ 400. To znatno povečanje učinkovitosti algoritma omogoča njegovo popolno uporabo. Na primer, algoritem Diffie-Hellman s tremi ali več člani.

Kakšna naj bo dolžina a

Pravilna izbira velikosti parametrov Diffie-Hellmanovega algoritma je precej zapletena naloga. Skupna zahteva v svetu kriptografije je na primer pogoj, da mora napadalec vdreti v sistem vsaj ^2.128 korakov. Če je v simetričnih algoritmih za šifriranje v skladu s takšno zahtevo precej enostavno, je v algoritmih javnega ključa to resničen problem. Če upoštevate zgornjo zahtevo, mora biti dolžina a sestavljena iz vsaj 850 bajtov.

V praksi ta velikost povzroča velike težave z zmogljivostjo v sistemu, saj operacije javnega ključa trajajo veliko dlje kot na primer pri simetričnem šifriranju s 128 ali 256 bitnimi ključi. Kako pa potem? Najmanjša dolžina javnega ključa se mora začeti pri 2048 bitih. Čeprav je ključ daljši, višja je raven varnosti. Upoštevati je treba predvsem uspešnost sistema in njegove stroške. Če vam omogoča uporabo ključa 4096 bitov, morate to storiti.

Kako se ocenjuje zahtevana stopnja varnosti?

Velikosti ključev v simetričnem šifriranju ostajajo nespremenjene (128, 256 bitov) celotno življenjsko dobo sistema, medtem ko so velikosti javnega ključa vedno spremenljive vrednosti. Če morate razviti sistem, ki ga morate uporabljati 30 let in hraniti podatke v tajnosti vsaj 20 let po tem, ko je bil sistem izločen iz uporabe, mora biti velikost simetričnega šifrirnega ključa na začetku dovolj velika, da zaščiti sistem za naslednjih 50 let.

Zaradi očitnih težav z zmogljivostjo, ker Diffie-Hellmanov algoritem šifrira veliko večje število operacij, se zahteve za javne ključe razlikujejo. Še vedno velja eno leto in podatke varuje za naslednjih 20 let, torej se uporablja skupno 21 let. Zaradi spremenljive velikosti se lahko ključ spreminja vsako leto in se vedno bolj ustvarja, da se zagotovi zahtevana raven varnosti.

Najboljše ocene na primer kažejo, da lahko ključ z dolžino 256 bajtov zagotovi zaščito podatkov za približno 20 let, dolžina 384 bajtov pa 35 let, z dolžino 512 bajtov pa je 47 let itd. ^{Za odpravo} je potrebnih ^2.128 korakov, ki izhajajo iz podobnih ocen. Vendar pa je to le napoved, ki jo morate zelo skrbno zaupati. Lahko precej natančno napovedati razvoj dogodkov za 10 let naprej, vendar na 50 - to je fantastično.

Praktična priporočila

Tu je nekaj praktičnih nasvetov o uporabi protokola DH. Izberite k kot prvo število 256 bitov. To je minimum, ki lahko zagotovi vsaj ustrezno raven varnosti pred napadi. Za a izberite število, ki bi imelo obliko Na + 1, kjer je N celo število. O velikosti števila a je bilo rečeno prej. Po tem se izbere naključno število b in se preveri za več pogojev. Prvič, ne more biti enota. Drugič, b ^k = 1.

Vsak udeleženec v komunikaciji pa mora biti prepričan o naslednjem:

• a in k sta primarni številki, dolžina k je 256 bitov, dolžina p je precej velika.
• število k je delitelj a-1.
• b ni enako 1 in b ^k = 1.

Te pogoje je treba preveriti tudi z brezpogojnim zaupanjem v vir.

Zaključek

DH algoritem je iznajdljiva rešitev enega resnih problemov in se še vedno aktivno uporablja v spremenjeni obliki za sodobne varnostne zahteve v različnih protokolih. Diffie-Hellmanov algoritem se na primer uporablja v nekaterih delih implementacije protokola IKE. Vendar pa mora biti njegova uporaba metodična in previdna zaradi prisotnosti očitnih težav in resnih pasti.