Algebraično napredovanje: formule in primeri rešitev
V članku bomo razpravljali o algebraični progresiji, formulah, ki so potrebne za reševanje problemov z njeno udeležbo, ter nekaj primerov njihove uporabe. Zaradi celovitosti bomo na kratko govorili o drugi vrsti napredovanja - geometrični.
Koncept algebrskega napredovanja

Vsako serijo številk, ki so urejene po nekem zakonu, lahko imenujemo napredovanje. Najbolj priljubljena in uporabljena za reševanje praktičnih problemov sta dve vrsti takšnih serij: algebraična in geometrijska progresija. Razmislite o prvi od njih podrobneje.
Algebraic se pogosto imenuje aritmetično napredovanje. Matematično pomeni:
a n = a n-1 + d
To pomeni, da govorimo o takšnem številčnem zaporedju, v katerem se katerikoli njegov član razlikuje od prejšnjega ali naslednjega z isto številko d. To število se imenuje razlika (lahko jo določimo z ugotovitvijo razlike med dvema sosednjima elementoma napredovanja).
V skladu s to definicijo ima obravnavano napredovanje začetek, vendar ne konca. Vedno se začne z izrazom a 1 (katero koli realno število) in nato nadaljuje s seštevanjem tega člana z razliko d. V skladu s tem je lahko neskončno naraščajoč (d> 0) ali se zmanjšuje (d <0). Položaj, ko je d = 0, lahko velja tudi za poseben primer aritmetičnega napredovanja, ki ga predstavlja neskončno zaporedje enakih števil.
Formula za iskanje poljubnega člana
Kot je bilo pojasnjeno zgoraj, je obravnavani tip napredovanja edinstveno določen s prvim elementom in razliko, vendar se to pravilo uporablja za vse druge vrednosti. Na primer, poznavanje dveh poljubnih elementov ali enega elementa in vsota določenega števila članov prav tako edinstveno določa napredovanje.
Za izračun n-tega elementa lahko uspešno uporabite naslednjo formulo:
a n = a 1 + (n - 1) * d
Očitnost veljavnosti tega izraza je nedvomna in vsak jo lahko preveri tako, da nadomesti majhne vrednosti n.
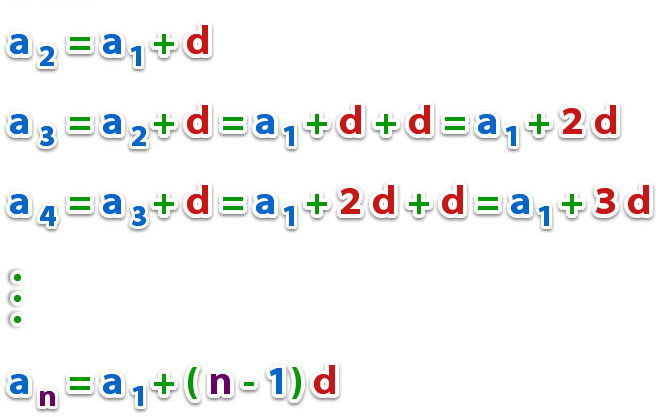
Formula za obnovitev napredovanja dveh znanih elementov
V šolskem poteku algebre so taki problemi značilni za napredovanje: obstajata dva elementa a n in a m , in n> m, potrebno je na njih zgraditi celotno napredovanje.
Ta problem je rešen s formulo za n-ti član. Izpišemo dva ustrezna izraza:
a n = a 1 + (n - 1) * d;
a m = a 1 + (m - 1) * d
Poiščite razliko med prvim in drugim (znak enakosti je ohranjen):
a n - a m = (n - m) * d =>
d = (a n - a m ) / (n - m)
Vidimo, kako preprosto je najti razliko napredovanja, če sta znana dva njena člana: za to odštej manjšega od večjega po vrsti in nato razdelimo nastalo razliko z razliko njihovih zaporednih številk.
Ko je razlika ugotovljena, je lahko prvi izračun izračunov (za to uporabite enega od prvih dveh izrazov).
Vsota algebrskega napredovanja
Druga vrsta tipičnih nalog za napredovanje je iskanje vsote njihovih članov. Naslednja formula je ustrezna algebraična formula za napredovanje:
S n = ∑ i = 1 n (a i ) = n * (a 1 + a n ) / 2
To pomeni, da za določitev vsote prvih členov n, je treba izračunati vsoto le dveh od njih (prvi in n), jo pomnožimo s številom članov n in razdelimo rezultat na polovico.
Matematični dokaz tega izraza izpuščamo, vendar še vedno dajemo logičen dokaz. Ugotovimo lahko, da glede na lastnost obravnavanega tipa napredovanja vedno velja naslednja enakost:
a 1 + a n = a 2 + a n-1
Drugi izraz je dejansko večji od prvega z d, toda z istim predzadnjim ( n-1 ) je manjši od zadnjega (a n ). V primeru para elementov dobimo natančno polovico takih vsot iz skupnega števila elementov (n / 2), iz česar sledi reducirana formula za S n .

Šteje se, da je omenjeno značilnost aritmetičnega napredovanja najprej vzpostavil Karl Gauss, slavni matematik s konca 18. - prve polovice 19. stoletja, ko je v svojih mislih za nekaj sekund izračunal vsoto naravnih števil od enega do 100.
Primeri reševanja problemov
Razmislite o dveh primerih algebrskega napredovanja.
1. Znano je, da je deveti mandat 7, 21 pa 51. Potrebno je najti prvih 5 članov te aritmetične progresije.
Pogoj problema nam omogoča, da takoj izračunamo razliko d, pri čemer uporabimo formulo z n in m , ki je zapisana zgoraj. Imamo:
d = (a n - a m ) / (n - m) = (51 - 7) / (21 - 9) = 3,667
Po prejemu razlike d smo izvedli zaokroževanje na tri decimalna mesta.
Zdaj lahko izračunate prvi element serije. V ta namen uporabite podatke za 9 članov:
a 9 = a 1 + d * 8 => a 1 = a 9 - d * 8 = 7 - 3,667 * 8 = -22,336
Za rešitev problema je še zadnji korak: dodajte zaporedno 4-kratno vrednost d prvemu elementu. Dobimo:
a 1 = -22.336;
a2 = -22,336 + 3,667 = -18,669;
a3 = -18.669 + 3.677 = -15.002;
a 4 = -15.002 + 3.667 = -11.335;
a 5 = -11,335 + 3,667 = -7,668
Spomnimo se, da so vse izračunane vrednosti veljavne do tretjega decimalnega mesta.
2. Delavci so zložili žagane drevesne debla v obliki piramide. Znano je, da so določili le 33 hlodov, do konca piramide pa so manjkali samo 3 hlodi. Treba je ugotoviti, koliko vrst hlodov položi delavci.
Odgovor na to vprašanje je rešiti algebraično napredovanje, toda, če želimo nadaljevati z njim, moramo to stanje skrbno obravnavati.
Prvič, ker se plošče seštevajo v piramido, to pomeni, da je bila v vsaki prejšnji vrstici še en dnevnik, to je d = 1. Drugič, če je znano, da manjkajo samo 3 hlodi, preden je piramida zaključena, potem ostanejo dve zgornji vrstici. prazno:
a 1 = 1, a 2 = a 1 + d = 2, a 1 + a 2 = 3
Upoštevamo te tri dnevnike, jih dodamo v že zložene 33 in določimo neznano število vrstic n, pri čemer uporabimo formule za vsoto in n-ti član:
S n = n * (a 1 + a n ) / 2; a n = a 1 + d * (n - 1) =>
S n = n * (a 1 + a 1 + d * (n - 1)) / 2 = (2 * a 1 - d) / 2 * n + d * n 2/2
Znane podatke nadomestimo z zadnjo enakostjo in rešimo dobljeno kvadratno enačbo za n:
36 = 0,5 * n + 0,5 * n2 ali
n 2 + n - 72 = 0
Diskriminator: D = 1 - 4 * 1 * (-72) = 289
Korenine: n = (-1 ± 17) / 2 = (8; -9)
Negativno vrednost bomo takoj zavrnili, ker nasprotuje stanju problema. Tako bo 8 vrstic piramide vsebovalo 36 dnevnikov. Ker delavci nista dokončali obeh zgornjih vrstic, pomeni, da sta se le dodali 6 vrstic hlodov.
Nekaj besed o napredovanju geometrije
Algebraično in geometrijsko napredovanje se praviloma obravnava v okviru ene teme, zato je koristno dati idejo o drugi vrsti zaporednih številskih serij. Geometrijska progresija je torej serija številk, ki spoštujejo zakon:
a n = a n-1 * r
To pomeni, da za razliko od aritmetike, da bi dobili vse elemente, ne smete dodati enega števila, ampak ga pomnožiti (r imenujemo imenovalec).
Iz definicije je razvidno, da geometrijska progresija raste (zmanjšuje) veliko hitreje kot aritmetična.
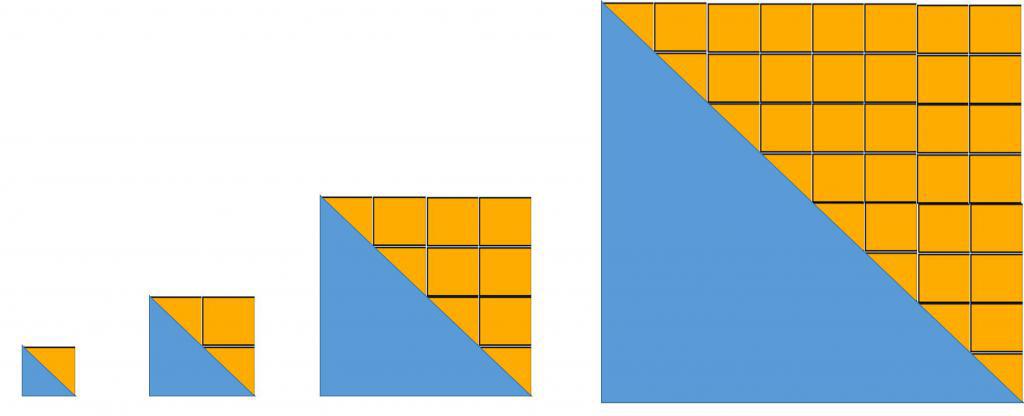
Pogosto se uporablja v geometriji, na primer pri izračunu površin številk z uporabo njihove delitve na ločene elemente (metoda delitve na pol).