Zgodovina Pitagorejevega izreka. Dokaz teorema

Tisti, ki jih zanima zgodovina pitagorejskega izreka, ki ga proučujemo v šolskem učnem načrtu, bodo prav tako radovedni, da bo leta 1940 objavljena knjiga s tristo sedemdesetimi dokazili tega navidez preprostega izreka. Toda intrigirala je um številnih matematikov in filozofov različnih obdobij. V Guinnessovi knjigi rekordov je določen kot izrek z največjim številom dokazov.

Zgodovina Pitagorejevega izreka

Povezan z imenom Pitagora, je bil teorem znan že pred rojstvom velikega filozofa. Tako se je v Egiptu med gradnjo struktur upoštevalo razmerje pravokotnega trikotnika pred pet tisoč leti. Babilonska besedila se nanašajo na isto razmerje stranic. pravokotni trikotnik 1200 let pred rojstvom Pitagore.

Postavlja se vprašanje, zakaj potem zgodba pravi - pojav Pitagorejevega izreka pripada njemu? Odgovor je lahko le eden - dokazal je razmerje v trikotniku. To, kar so pred stoletji naredili tisti, ki so preprosto uporabljali razmerje stranic in hipotenuza, ki so jo empirično vzpostavili, ni storila.

Iz življenja Pitagore

Prihodnost velika znanstvenik, matematik, Filozof se je rodil na otoku Samos leta 570 pred našim štetjem. Zgodovinski dokumenti so ohranili podatke o očetu Pitagore, ki je bil rezbar za dragocene kamne, vendar o mami ni podatkov. Govorili so o fantu, ki se je rodil, da je bil izreden otrok, ki je od otroštva pokazal strast do glasbe in poezije. Zgodovinarji pripisujejo učitelje mladih Pitagore Herdomadantu in Ferekidu Syrosu. Prvi je dečka predstavil v svetu muze, drugi, ki je bil filozof in ustanovitelj italijanske filozofske šole, je mladeniča pogled usmeril proti logotipom.

Pri 22 letih (548 pr. N. Št.) Je Pitagora odšel v Nookratis, da bi preučil jezik in vero Egipčanov. Nadalje, njegova pot je ležala v Memphisu, kjer je, zahvaljujoč duhovnikom, potem ko je preživel svoje genialne teste, spoznal egiptovsko geometrijo, ki je morda spodbudila radovednega mladeniča, da dokaže Pitagorov izrek. Zgodovina bo ta izrek pripisala izreku v prihodnosti.

Ujet je kralj Babilon

Na poti domov v Helijo kralj Babilon ujame Pitagora. Ampak biti v ujetništvu koristil radovedni um začetnika matematika, imel je nekaj za učenje. Dejansko je bila v teh letih matematika v Babilonu bolj razvita kot v Egiptu. Dvanajst let je študiral matematiko, geometrijo in magijo. In verjetno je bila babilonska geometrija vpletena v dokazovanje razmerja stranic in zgodovino odkritja teorema. Za to je imel dovolj znanja in časa. Toda, da se je to zgodilo v Babilonu, ni dokumentarne potrditve ali izpodbijanja.

530 leta pr Pitagora pobegne iz ujetništva v svojo domovino, kjer živi na dvorišču tiranina Polycratesa v statusu pol-plošče. Takšno življenje ne ustreza Pitagori in se umika v jame Samosa, nato pa gre na jug Italije, kjer se je takrat nahaja grška kolonija Croton.

Tajni redovni red

Na podlagi te kolonije je Pitagora organiziral tajno redovno ureditev, ki je bila hkrati verska zveza in znanstvena družba. Ta družba je imela svojo listino, ki se je nanašala na spoštovanje določenega načina življenja.

Pitagora je trdil, da se mora človek za razumevanje Boga naučiti takih znanosti kot algebra in geometrija, poznati astronomijo in razumeti glasbo. Raziskovalno delo je bilo omejeno na poznavanje mistične strani številk in filozofije. Poudariti je treba, da so načela, ki jih je v tistem času pripovedoval Pitagora, smiselna že v posnemanju.

Veliko odkritij, ki so jih naredili učenci Pitagore, so mu pripisali. Kljub temu, če govorimo na kratko, je zgodovina nastanka Pitagorejevega izreka antičnih zgodovinarjev in biografov tistega časa neposredno povezana z imenom tega filozofa, misleca in matematika.

Učenja Pitagore

Morda je misel o povezavi teorema z imenom Pitagore nagnala zgodovinarje, da pravijo veliki Grki, da so vsi fenomeni našega življenja kodirani v notorni trikotnik z njegovimi nogami in hipotenuzo. In ta trikotnik je "ključ" za rešitev vseh problemov, ki se pojavijo. Veliki filozof je rekel, da bi bilo treba videti trikotnik, potem lahko domnevamo, da je problem rešen dve tretjini.

Pitagora je govoril o svojem poučevanju le ustno svojim učencem, ne da bi zapisoval, da je to skrivnost. Na žalost, učenje največjega filozofa še danes ni preživelo. Nekaj ​​od njega je izteklo, vendar ne moremo reči, koliko je resnično in koliko je napačno, kar je postalo znano. Tudi z zgodovino Pitagorejevega izreka ni vse nesporno. Zgodovinarji matematike dvomijo v avtorstvo Pitagore, po njihovem mnenju je bil teorem uporabljen več stoletij pred njegovim rojstvom.

Pitagorov izrek

Morda se zdi čudno, vendar Pitagorin sam teorem ne pozna nobenega zgodovinskega dokaza - ne v arhivu, niti v drugih virih. V sodobni verziji velja, da pripada nihče drug kot Euclid sam.

Obstajajo dokazi, da je eden od največjih zgodovinarjev matematike Moritz Cantor, ki je odkril na papirusu, shranjenem v berlinskem muzeju, zabeležili Egipčani okoli leta 2300 pred našim štetjem. e. enakost, ki se glasi: 3² + 4² = 5².

Na kratko iz zgodovine Pitagorejevega izreka

Formulacija izreka iz evklidskih "načel" v prevodu se sliši enako kot v sodobni interpretaciji. V njem ni novega branja: kvadrat na nasprotni strani pravokotnega kota je enak vsoti kvadratov stranic, ki ležijo ob desnem kotu. Dejstvo, da so starodavne civilizacije Indije in Kitajske uporabile ta izrek, potrjuje razprava Zhou - bi suan jin. Vsebuje informacije o egiptovskem trikotniku, ki opisuje razmerje 3: 4: 5.

Nič manj zanimiva je še druga kitajska matematična knjiga, Chu-Pei, ki omenja tudi pitagorejski trikotnik z razlago in risbami, ki sovpadajo z risbami hindujske geometrije Bashare. O samem trikotniku v knjigi je zapisano, da če je pravi kot lahko razčlenjen na njegove sestavne dele, bo linija, ki povezuje konce stranic, enaka petim, če je osnova tri, višina pa štiri.

Indijska razprava "Sulva sutra", ki sega v obdobje VII-V stoletja pr. govori o izgradnji pravih kotov z uporabo egiptovskega trikotnika.

Dokaz teorema

V srednjem veku so študenti preveč težko dokazovali dokazovanje teorema. Slabi učenci so si na pamet zapisali teoreme, ne da bi razumeli pomen dokaza. V zvezi s tem so prejeli vzdevek "osli", ker je bil pitagorejski izrek za njih nepremostljiva ovira, kot most za rit. V srednjem veku so študentje pripravili verz na šali o tem teoremu.

Da bi dokazali Pitagorejski izrek na najlažji način, bi morali preprosto izmeriti njegove strani, ne da bi uporabili koncept kvadratov v dokazu. Dolžina nasprotne pravokotne strani je c, sosednje a in b pa dobimo enačbo: a ² + b ² = c ² . Ta izjava, kot je omenjeno zgoraj, se preveri z merjenjem dolžin strani pravokotnega trikotnika.

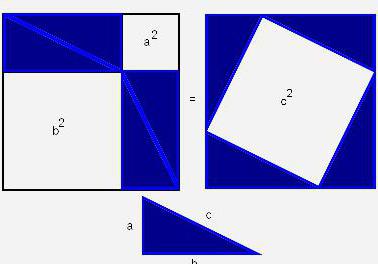
Če pričnemo dokazovanje izreka z upoštevanjem površine pravokotnikov, zgrajenih na straneh trikotnika, lahko določimo območje celotne figure. To je enako površini kvadrata s stranico (a + b), na drugi strani pa vsoto površin štirih trikotnikov in notranjega kvadrata.

(a + b) ² = 4 x ab / 2 + c ² ;

a ² + 2ab + b ² ;

c ² = a ² + b ² , kot se zahteva.

Praktični pomen Pitagorejevega izreka je, da ga lahko uporabimo za iskanje dolžin segmentov, ne da bi jih merili. Med gradnjo stavb se izračunajo razdalje, postavitev nosilcev in nosilci, določijo se težišča. Pitagorejski izrek se uporablja v vseh sodobnih tehnologijah. Pri ustvarjanju filmov v 3D-6D-dimenzijah nismo pozabili na izrek, kjer se poleg treh običajnih vrednosti upoštevata višina, dolžina, širina - čas, vonj in okus. Kako so okusi in vonji povezani s teoremom? To je zelo preprosto - ko pokažete film, morate izračunati, kje in kaj smrdi in okusi poslati v avditorij.

Ali bo še vedno. Neomejen prostor za odkrivanje in ustvarjanje novih tehnologij pričakuje spraševalne misli.