Paralelnost ravnin: znak, stanje

Vsakdo, ki je kdajkoli študiral ali se trenutno izobražuje v šoli, se je moral soočiti z različnimi težavami pri študiju disciplin, ki so vključene v program, ki ga je razvilo Ministrstvo za šolstvo.

S katerimi težavami se soočamo

Učenje jezikov spremlja spomin na obstoječa slovnična pravila in glavne izjeme. Fizična vzgoja zahteva veliko izračunov, fizične pripravljenosti in veliko potrpljenja študentov.

Vendar pa je nemogoče primerjati z vsemi težavami, ki se pojavijo pri proučevanju natančnih disciplin. Algebra vsebuje zapletene načine reševanja osnovnih problemov. Fizika z bogatim nizom formul fizikalnih zakonov. Geometrija in njeni odseki, ki temeljijo na kompleksnih izrekih in aksiomih.

Primer so aksiomi, ki razlagajo teorijo paralelizma ravnin, ki jo je treba nujno zapomniti, saj temeljijo na celotnem poteku šolskega kurikuluma v stereometriji. Poskusimo ugotoviti, kako je to lažje in hitreje.

Vzporedne ravnine s primeri

Aksiom, ki kaže paralelnost ravnin, se glasi: " Vsaka dva ravnina se šteje za vzporedna samo, če ne vsebujejo skupnih točk, " kar pomeni, da se med seboj ne sekata. Da bi si to sliko predstavljali bolj podrobno, lahko kot osnovni primer navedemo razmerje med stropom in tlemi ali nasprotnimi stenami v stavbi. Takoj je jasno, kaj je mišljeno, in potrjuje tudi dejstvo, da se v običajnem primeru te ravnine nikoli ne bodo križale.

Drugi primer je okensko steklo, kjer steklene mreže delujejo kot ravnine. Prav tako v nobenem primeru ne bodo tvorile križišč. Poleg tega lahko dodate knjižne police, Rubikovo kocko, kjer so ravnine njeni nasprotni obrazi, in drugi elementi vsakdanjega življenja.

Zadevne ravnine so označene s posebnim znakom v obliki dveh ravnih črt "||", ki jasno ponazarjata vzporednost ravnin. Tako lahko z uporabo realnih primerov oblikujemo jasnejšo percepcijo teme in posledično lahko nadaljujemo z obravnavanjem kompleksnejših konceptov.

Kje in kako se uporablja teorija vzporednih ravnin?

Študentje se pri študiju geometrije soočajo z mnogostranskimi problemi, kjer je pogosto potrebno določiti vzporednost linij, linij in ravnin med seboj ali odvisnost ravnin med seboj. Vsako nalogo lahko analiziramo s štirimi glavnimi razredi stereometrije.

Prvi razred vključuje naloge, pri katerih je potrebno določiti vzporednost črte in ravnine med seboj. Njegova rešitev se zniža na dokazovanje enakega izreka. V ta namen je treba ugotoviti, ali obstaja v tej ravnini vzporedna premica za premico, ki ne pripada zadevni ravnini.

Drugi razred nalog vključuje tiste, pri katerih je vključena značilnost vzporednosti ravnin. Uporablja se za poenostavitev postopka dokazovanja, s čimer se bistveno skrajša čas za iskanje rešitve.

Naslednji razred pokriva obseg problemov skladnosti z neposrednimi osnovnimi lastnostmi vzporednosti ravnin. Rešitev problemov četrtega razreda je določanje, ali je izpolnjen pogoj vzporednosti ravnin. Če natančno vemo, kako se dokaže določen problem, je učencem lažje navigirati, ko uporabljajo obstoječi arzenal geometrijskih aksiomov.

Tako se naloge, katerih pogoj zahteva definiranje in dokazovanje vzporednosti ravnih črt, ravne črte in ravnine ali dveh ravnin med njimi, zmanjšajo na pravilen izbor teorema in rešitev v skladu z obstoječim sklopom pravil.

O vzporednosti črte in ravnine

Paralelnost ravne črte in ravnine je posebna tema v stereometriji, saj je to temeljni koncept, na katerem temeljijo vse nadaljnje lastnosti paralelnosti geometrijskih figur.

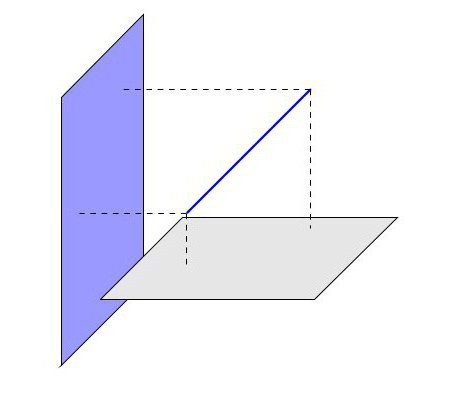
V skladu z obstoječimi aksiomi, v primeru, ko dve točki ravne črte pripadata določeni ravnini, lahko sklepamo, da je v njej tudi ta ravna črta. V tem primeru postane jasno, da obstajajo tri možnosti za lokacijo ravne črte glede na ravnino v prostoru:

1. Linija pripada letalu.
2. Za ravno črto in ravnino je ena skupna presečišče.
3. Za ravno črto in ravnino ni prisotnih presečišč.

Zlasti nas zanima zadnja možnost, ko ni stičišč. Šele takrat lahko rečemo, da sta premica in ravnina med seboj vzporedni. Tako se potrdi stanje glavnega izreka o vzporednem znaku ravne črte in ravnine, ki pravi, da: "Če je ravna črta, ki ne spada v obravnavano ravnino, vzporedna katerikoli ravni črti na tej ravnini, potem je pravica prav tako vzporedna tej ravnini".

Potreba po uporabi značilnosti paralelizma

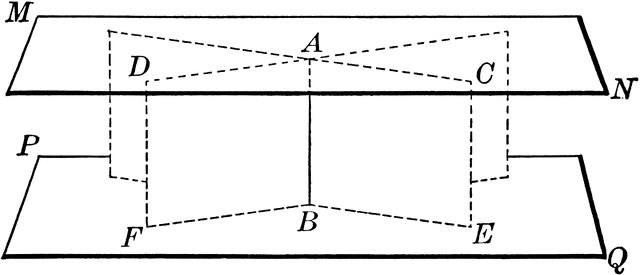
Znak paralelnosti ravnin se praviloma uporablja za iskanje poenostavljene rešitve problemov o ravninah. Bistvo te funkcije je naslednje: " Če sta v eni ravnini dve križani črti, ki se križata, vzporedno z dvema ravnima črtama, ki pripadata drugi ravnini, se lahko takšne ravnine imenujejo paralelne ."

Dodatni izreki

Poleg uporabe znaka, ki dokazuje vzporednost ravnin, se lahko v praksi srečate tudi z uporabo dveh dodatnih dodatnih izrekov. Prva je predstavljena v naslednji obliki: » Če je ena od vzporednih ravnin vzporedna s tretjo, potem je druga ravnina vzporedna s tretjo ali popolnoma sovpada z njo «.

Na podlagi uporabe reducibilnih izrekov je mogoče vedno dokazati vzporednost ravnin glede na obravnavani prostor. Drugi izrek prikazuje odvisnost ravnin od pravokotne ravne črte in izgleda kot: " Če sta dve neskladni ravnini pravokotni glede na neko ravno črto, potem se obravnavata vzporedno drug z drugim ".

Pojem potrebnih in zadostnih pogojev

Pri reševanju problemov večkratnega dokazovanja vzporednosti ravnin je bil izpeljan potreben in zadosten pogoj za vzporednost ravnin. Znano je, da je katera koli ravnina podana z parametrično enačbo oblike: A ₁ x + B ₁ y + C ₁ z + D ₁ = 0. Naš pogoj temelji na uporabi sistema enačb, ki definirajo razporeditev ravnin v prostoru in je predstavljen z naslednjim besedilom: " Da bi dokazali vzporednost dveh ravnin, je potrebno in zadostno, da je sistem enačb, ki opisuje te ravnine, nezdružljiv, to je, da nima rešitve ."

Osnovne lastnosti

Pri reševanju geometrijskih problemov pa uporaba paralelizma ni vedno dovolj. Včasih pride do situacije, ko je potrebno dokazati vzporednost dveh ali več vrstic v različnih ravninah ali enakost segmentov, zaprtih na teh linijah. V ta namen uporabite lastnosti vzporednih ravnin. V geometriji sta samo dve.

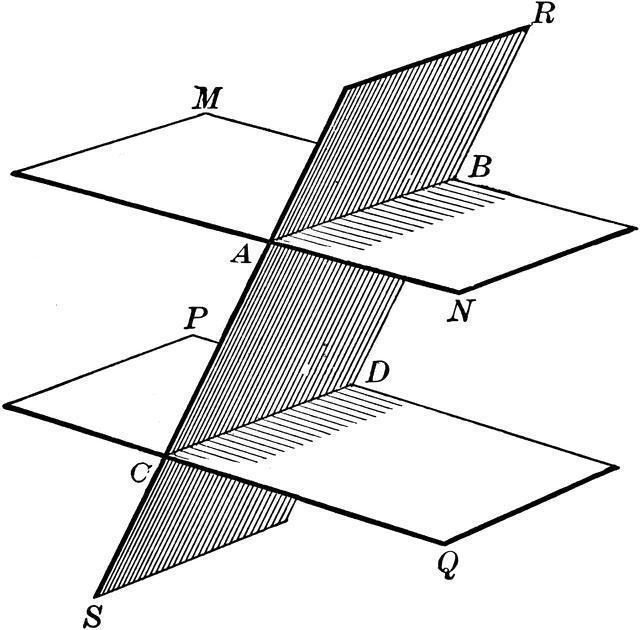
Prva lastnost nam omogoča, da presodimo vzporednost linij v določenih ravninah in jo predstavimo v naslednji obliki: " Če se dve vzporedni ravnini sekajo tretji, bodo linije, ki jih tvorijo presečišča, prav tako vzporedne ."

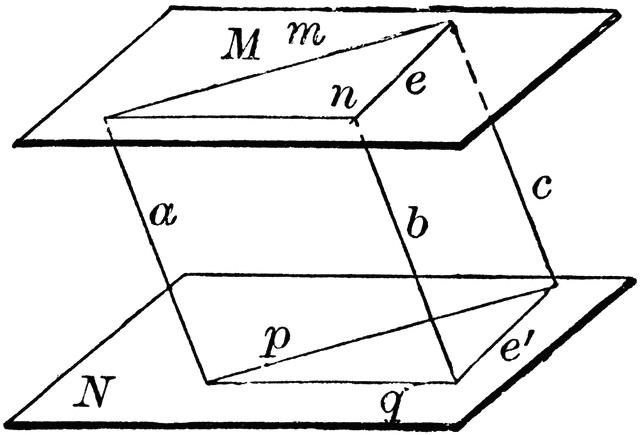
Pomen druge lastnosti je dokazati enakost segmentov, ki se nahajajo na vzporednih ravnih črtah. Njegova razlaga je predstavljena v nadaljevanju. " Če upoštevamo dve vzporedni ravnini in zaokrožimo regijo med njimi, potem lahko trdimo, da bo dolžina segmentov, ki jih tvori ta regija, enaka ."