Linearne enačbe: formule in primeri. Neenakosti in njihova rešitev
Učenje reševanja enačb je ena glavnih nalog, ki jo algebra predstavlja za študente. Začenši od najenostavnejšega, ko je sestavljen iz enega neznanega in se premakne na vse bolj kompleksno. Če se dejanja, ki jih je treba izvesti z enačbami iz prve skupine, ne razumejo, bo težko obravnavati druge.
Za nadaljevanje pogovora se morate dogovoriti o zapisu.
| Ime vrednosti | Njegovo ime |
| spremenljivko | x, y |
| katero koli številko | a, b, c |
Splošni pogled na linearno enačbo z eno neznano in načelo njene rešitve
Vsaka enačba, ki lahko vodi do zapisa te vrste:
a * x = v ,
imenovano linearno . To je splošna formula. Pogosto pri nalogah so linearne enačbe napisane implicitno. Nato morate izvesti identične transformacije, da dobite splošno sprejet zapis. Ta dejanja vključujejo:
- odpiranje oklepajev;
- premik vseh izrazov z spremenljivko na levo stran enačbe, ostalo pa na desno;
- takšne pogoje.
V primeru, ko je neznana vrednost v imenovalcu ulomka, je treba določiti njene vrednosti, pri katerih izraz nima smisla. Z drugimi besedami, potrebno je poznati domeno enačbe.
Načelo, po katerem se rešujejo vse linearne enačbe, se zniža na delitev vrednosti na desni strani enakosti s koeficientom pred spremenljivko. To pomeni, da bo "x" enako / a.
Posebni primeri linearne enačbe in njihove rešitve
Med razmišljanjem se taki momenti lahko pojavijo, ko linearne enačbe vzamejo eno od posebnih tipov. Vsaka od njih ima posebno rešitev.
V prvem primeru:
a * x = 0 , poleg tega pa a. 0.
Rešitev takšne enačbe bo vedno x = 0.
V drugem primeru je vrednost "a" enaka nič:
0 * x = 0 .
Odgovor na to enačbo bo poljubno število. To pomeni, da ima neskončno število korenin.
Tretja situacija izgleda takole: t
0 * x = in , kjer je v. 0.
Ta enačba nima smisla. Ker korenine, ki ga izpolnjujejo, ne obstajajo.

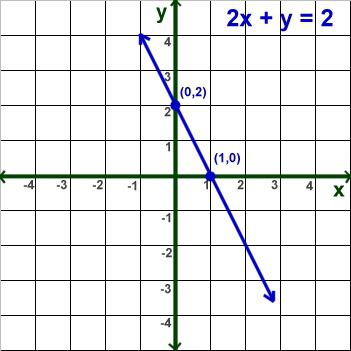
Splošni pogled na linearno enačbo z dvema spremenljivkama
Iz njenega imena postane jasno, da je v njej že dve neznani količini. Linearne enačbe z dvema spremenljivkama izgledata takole:
a * x + v * y = s .
Ker sta v zapisu dva neznanka, bo odgovor videti kot par številk. To ni dovolj za določitev samo ene vrednosti. To bo nepopoln odgovor. Par količin, pri katerih se enačba spremeni v identiteto, je rešitev enačbe. Poleg tega je odgovor vedno prvi, da zapišemo spremenljivko, ki poteka prej po abecednem vrstnem redu. Včasih pravijo, da mu te številke zadoščajo. Poleg tega so lahko ti pari neskončno število.
Kako rešiti linearno enačbo z dvema neznankama?
Če želite to narediti, vzemite kateri koli par številk, ki se izkaže za resničen. Za poenostavitev lahko vzamete eno od neznank, ki je enako vsem prvo število in nato poiščite drugo.
Pri reševanju je pogosto potrebno izvesti ukrepe za poenostavitev enačbe. Imenujejo se transformacije identitete. Poleg tega so za enačbe vedno veljavne naslednje lastnosti:
- vsak izraz se lahko prenese na nasprotni del enakosti z zamenjavo njegovega znaka z nasprotnim;
- levo in desno stran katere koli enačbe je dovoljeno deliti z isto številko, če ni enaka nič.

Primeri nalog z linearnimi enačbami
Prva naloga. Reši linearne enačbe: 4x = 20, 8 (x - 1) + 2x = 2 (4 - 2x); (5x + 15) / (x + 4) = 4; (5x + 15) / (x + 3) = 4.
V enačbi, ki je prva na tem seznamu, je dovolj, da 20 enostavno razdelimo na 4. Rezultat je 5. To je odgovor: x = 5.
Tretja enačba zahteva, da se izvede transformacija identitete. Sestavljen bo iz razkritja oklepajev in uvajanja takih pogojev. Po prvem dejanju enačba dobi obliko: 8x - 8 + 2x = 8 - 4x. Potem morate prenesti vse neznane na levo stran enakosti, ostalo pa na desno. Enačba bo izgledala takole: 8x + 2x + 4x = 8 + 8. Po zmanjšanju takšnih izrazov: 14x = 16. Zdaj izgleda enako kot prva in njena rešitev je enostavna. Odgovor je x = 8/7. Toda v matematiki naj bi celoten del razdelil napačen delež. Nato se bo rezultat preoblikoval, "x" pa bo enaka eni in eni sedmi.
V preostalih primerih so spremenljivke v imenovalcu. To pomeni, da morate najprej vedeti, pri katerih vrednostih so enačbe definirane. Za to morate izključiti številke, pri katerih se imenovalci spreminjajo na ničlo. V prvem primeru je to »-4«, v drugem pa »-3«. Te vrednosti je treba izključiti iz odgovora. Po tem morate obe strani enačbe pomnožiti z izrazi v imenovalcu.
Odprtje oklepajev in podajanje podobnih izrazov v prvi od teh enačb dobimo: 5x + 15 = 4x + 16, v drugem pa 5x + 15 = 4x + 12. Po transformacijah je rešitev prve enačbe x = -1. Drugi je enak "-3", kar pomeni, da slednji nima rešitve.
Druga naloga. Rešimo enačbo: -7x + 2y = 5.
Recimo, da je prvi neznani x = 1, potem enačba dobi obliko -7 * 1 + 2y = 5. Ko je faktor “-7” prenesen na desno stran enačbe in spremeni znak na plus, se izkaže, da je 2u = 12. Zato y = 6. Odgovor: ena od rešitev enačbe je x = 1, y = 6.

Splošni pogled na neenakost z eno spremenljivko
Vse možne situacije za neenakosti so predstavljene tukaj:
- a * x> in;
- a * x <v;
- a * x ≥ v;
- a * x ≤v.
Na splošno je videti kot najpreprostejša linearna enačba, le neenakost se nadomesti z znakom enakovrednosti.
Identična pravila preoblikovanja za neenakost
Tako kot linearne enačbe in neenakosti lahko spreminjamo po določenih zakonih. Zgodi se na naslednje:
- na levo in desno stran neenakosti se lahko doda kateri koli dobesedni ali numerični izraz, pri čemer znak neenakosti ostane enak;
- možno je tudi pomnožiti ali deliti z istim pozitivnim številom, ponovno se znak ne spremeni;
- pri množenju ali delitvi z istim negativnim številom ostane enakost resnična, če se znak neenakosti obrne.

Splošni pogled na dvojne neenakosti
Naslednje težave neenakosti so lahko predstavljene v težavah:
- v <a * x <s;
- v ≤ a * x <s;
- v <a * x ≤ s;
- v ≤ a * x ≤ c.
Dvojno se imenuje, ker je omejeno z znaki neenakosti na obeh straneh. Rešeno je z uporabo enakih pravil kot običajne neenakosti. In iskanje odgovora sega do številnih enakih transformacij. Dokler ne prejmemo najpreprostejšega.
Značilnosti reševanja dvojnih neenakosti
Prva od teh je njena slika na koordinatni osi. Te metode ni treba uporabiti za preproste neenakosti. Toda v težkih primerih je to preprosto potrebno.
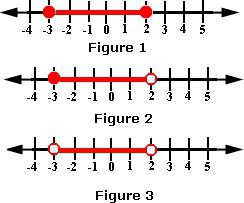
Za podobo neenakosti je potrebno na osi označiti vse točke, ki so se pojavile med razmišljanjem. To sta neveljavni vrednosti, ki ju označujeta punktirani točki, in vrednosti iz neenakosti, dobljene po transformacijah. Tudi tukaj je pomembno, da pravilno narišete točke. Če je neenakost stroga, to je <or>, potem so te vrednosti preluknjane. Pri šibkih neenakostih morajo biti točke obarvane.
Nato je treba označiti pomen neenakosti. To je mogoče storiti z valjenjem ali loki. Njihovo presečišče bo pokazalo odgovor.
Druga značilnost je povezana z njegovim zapisom. Tu sta dve možnosti. Prva je končna neenakost. Drugi je v obliki vrzeli. Zdi se mu, da se pojavijo težave. Intervali odgovora vedno izgledajo kot spremenljivka z znakom pripadnosti in oklepaji s številkami. Včasih obstaja več vrzeli, nato pa med oklepaji morate napisati simbol »in«. Ti znaki so naslednji: ∈ in ∩. Pomembno vlogo imajo tudi razmik med oklepaji. Prvi krog je nastavljen, ko je točka izključena iz odgovora, pravokotna pa vključuje to vrednost. Znak neskončnosti je vedno v oklepajih.
Primeri reševanja neenakosti
1. Rešite neenakost 7 - 5x ≥ 37.
Po preprostih transformacijah se izkaže: -5x ≥ 30. Če delimo s “-5”, dobimo naslednji izraz: x ≤ -6. To je odgovor, vendar ga lahko napišemo na drug način: x ∈ (-∞; -6].
2. Rešite dvojno neenakost -4 <2x + 6 ≤ 8.
Najprej morate odštevati vse 6. Izkazalo se je: -10 <2x ≤ 2. Sedaj morate razdeliti na 2. Neenakost bo izgledala kot: -5 <x ≤ 1. Ko je prikazan odgovor na številski osi, lahko takoj razumete, da bo rezultat od -5 do 1. In prva točka je izključena, druga pa je vključena. To pomeni, da je odgovor na neenakost: x ∈ (-5; 1]).