Kako najti kvadratni koren? Lastnosti, primeri ekstrakcije korena

Matematika je nastala, ko je oseba spoznala sebe in se začela postavljati kot avtonomna enota sveta. Želja, da izmerimo, primerjamo, izračunamo, kaj vas obdaja - je bila osnova ene od temeljnih znanosti naših dni. Sprva so bili to elementi elementarne matematike, ki so nam omogočali povezovanje številk z njihovimi fizičnimi izrazi, poznejše ugotovitve pa so bile predstavljene samo teoretično (zaradi njihove abstraktnosti), torej, čez nekaj časa, kot je dejal en znanstvenik, vse številke. " Koncept "kvadratnega korena" se je pojavil v času, ko bi ga lahko zlahka podprli empirični podatki, ki bi presegali ravnino izračuna.

Kako se je vse začelo

Prva omemba korena, ki je trenutno označena kot √, je bila zabeležena v spisih babilonskih matematikov, ki so začeli sodobno aritmetiko. Seveda so izgledali nekoliko podobni sedanji obliki - znanstveniki iz teh let so sprva uporabljali kosovne tablete. Toda v drugem tisočletju pr. e. izpeljali so približen izračun, ki je pokazal, kako izločiti kvadratni koren. Na spodnji sliki je kamen, na katerem so babilonski znanstveniki izločili proces ,2, in izkazalo se je, da je tako res, da je bila razlika v odgovoru najdena le na desetem decimalnem mestu.

Poleg tega je bil uporabljen tudi koren, če je bilo treba najti stran trikotnika, pod pogojem, da sta znana druga dva. No, ko se odločamo kvadratne enačbe Od pridobivanja korenine ne more iti nikamor.

Skupaj z babilonskimi deli je bil predmet članka proučevan tudi v kitajskem delu "Matematika v devetih knjigah", stari Grki pa so prišli do zaključka, da vsako število, iz katerega se ne izvleče korenine brez preostanka, daje iracionalen rezultat.

Izvor tega izraza je povezan z arabsko predstavitvijo števila: stari učenjaki so verjeli, da kvadrat poljubne številke raste iz korena, kot rastlina. V latinščini ta beseda zveni kot radix (lahko sledite vzorcu - vse, kar ima koren, pomeni obremenitev, je soglasno, pa naj gre za redkev ali radikulitis).

Znanstveniki naslednje generacije so to zamisel izbrali kot Rx. Na primer, v XV. Stoletju, da bi nakazali, da je kvadratni koren vzet iz poljubne številke a, so napisali R ² a. Znan »klop« se je pojavil šele v 17. stoletju, zahvaljujoč Reneju Descartesu.

Naši dnevi

Z vidika matematike je kvadratni koren y tako število z, katerega kvadrat je enak y. Z drugimi besedami, z ² = y je enakovredno =y = z. Vendar pa je ta definicija pomembna le za aritmetični koren, saj pomeni ne-negativno vrednost izraza. Z drugimi besedami, =y = z, kjer je z večji ali enak 0.

Na splošno velja, da je vrednost izraza lahko pozitivna in negativna tako, da se definira algebrski koren. Torej zaradi dejstva, da je z ² = y in (-z) ² = y, imamo: =y = ± z ali =y = | z |.

Zaradi dejstva, da se je ljubezen do matematike z razvojem znanosti samo povečala, obstajajo različne manifestacije naklonjenosti do nje, ki niso izražene v suhem računanju. Na primer, enako s tako zabavnimi pojavi, kot je dan Pi, se praznujejo tudi prazniki kvadratnega korena. Označene so devetkrat v sto letih in so določene po naslednjem načelu: številke, ki označujejo dan in mesec, morajo biti kvadratni koren leta. Torej, naslednjič bomo praznovali ta praznik 4. aprila 2016.

Lastnosti kvadratnega korena na polju R

1. Kvadratni koren izdelka je enak izdelku kvadratnih korenov, če so radikalni izrazi večji ali enak 0.
2. Ko postavimo kvadratni koren, je dovolj, da na to moč postavimo radikalen izraz, pod pogojem, da je večji od nič.
3. Kvadratni koren frakcije je enak korenu števca, deljenega s korenom imenovalca, pod pogojem, da je kvadratni koren števca večji ali enak 0, kvadratni koren imenovalca pa je strogo večji od 0.
4. Radikalni izraz, če je večji od nič, je mogoče razdeliti na več delov, iz katerih je dovoljeno izvleči koren. Na primer: =75 = *25 * 3 = 5√3.
5. Pod znakom korena lahko vnesete poljubno število in ga dvignete na kvadrat. Na primer: 5√8 = *25 * =8 = .200.

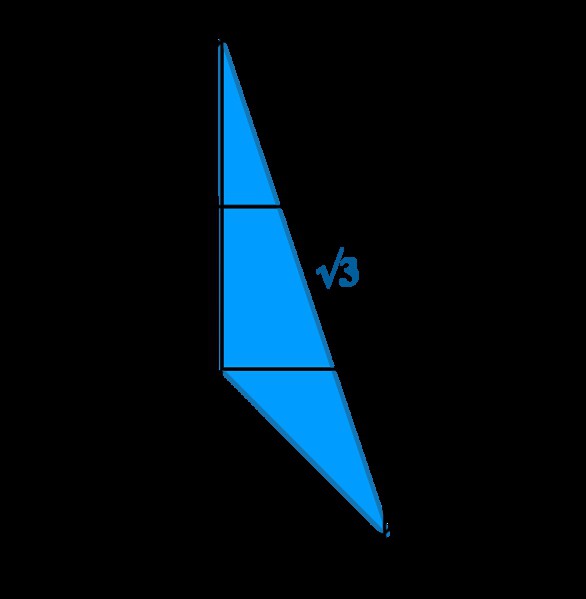
Praktično vsi matematični izrazi imajo pod njimi geometrijsko osnovo, ta usoda in ,y, ki je opredeljena kot stran kvadrata z območjem y, ni pobegnila.

Kako najti koren številke?

Obstaja več algoritmov za računalništvo. Najbolj preprosta, a precej okorna je običajno aritmetično izračunavanje, ki vsebuje naslednje:

1) od števila, katerega koren potrebujemo, se odštejejo lihih števil - dokler izhodna bilanca ni manjša od odbitne ali celo nič. Število premikov in bo sčasoma želena številka. Na primer, izračun kvadratnega korena 25:

25-1 = 24

24-3 = 21

21-5 = 17

17-7 = 10

10-9 = 1

Naslednje neparno število je 11, ostalo je naslednje: 1 <11. Število premikov je 5, tako da je koren 25 je 5. Vse se zdi, da je enostavno in enostavno, vendar si predstavljajte, kaj morate izračunati iz 18769? 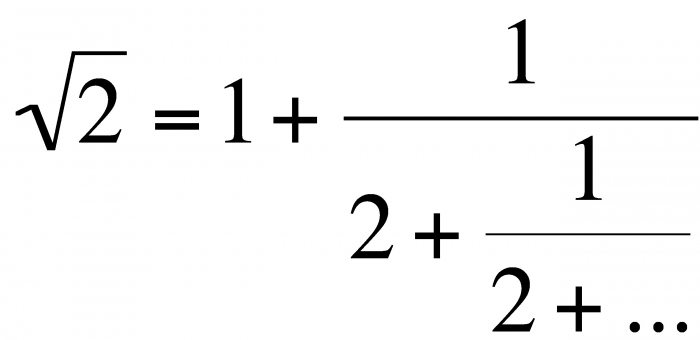V takih primerih je v Taylorjevi seriji razgradnja:

√ (1 + y) = ∑ ((- 1) ⁿ (2n)! / (1-2n) (n!) ² (4 ⁿ )) y ⁿ , kjer n ima vrednosti od 0 do

+ ∞ in | y | ≤1.

Grafični prikaz funkcije z = .y

Razmislite o elementarni funkciji z = √y na polju realnih števil R, kjer je y večji ali enak nič. Njen urnik je naslednji: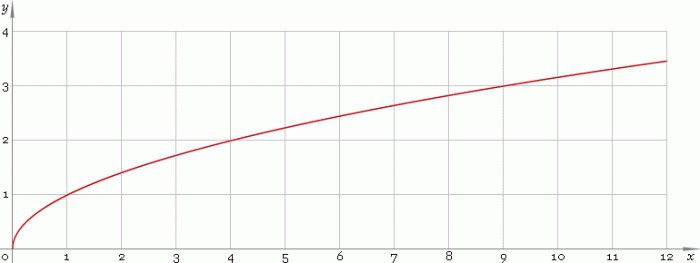

Krivulja raste od izvora in nujno prečka točko (1; 1).

Lastnosti funkcije z = √y na polju realnih števil R

1. Domena obravnavane funkcije je interval od nič do plus neskončnosti (nič je vključen).

2. Obseg vrednosti zadevne funkcije je interval od nič do plus neskončnosti (ničelna vrednost je ponovno vključena).

3. Najmanjša vrednost (0) funkcije je samo na točki (0; 0). Največja vrednost manjka.

4. Funkcija z = √y ni niti ne niti neparna.

5. Funkcija z = √y ni periodična.

6. Presečišče grafa funkcije z = √y z osmi koordinat je samo eno: (0; 0).

7. Presečišče grafa funkcije z = √y je tudi nič te funkcije.

8. Funkcija z = continuouslyy nenehno raste.

9. Funkcija z = √y vzame le pozitivne vrednosti, zato njen graf zavzema prvi koordinatni kot.

Različice funkcije slike z = √y

V matematiki je za lažje izračunavanje kompleksnih izrazov včasih uporabljena oblika moči za pisanje kvadratnega korena: =y = y ^1/2 . Takšna možnost je primerna, na primer pri dvigu funkcije na moč: ()y) ⁴ = (y ^1/2 ) ⁴ = y ² . Ta metoda je tudi dobra ideja za diferenciacijo z integracijo, saj je zaradi nje kvadratni koren predstavljen z navadno funkcijo moči.

Pri programiranju je zamenjava znaka √ kombinacija črk sqrt. 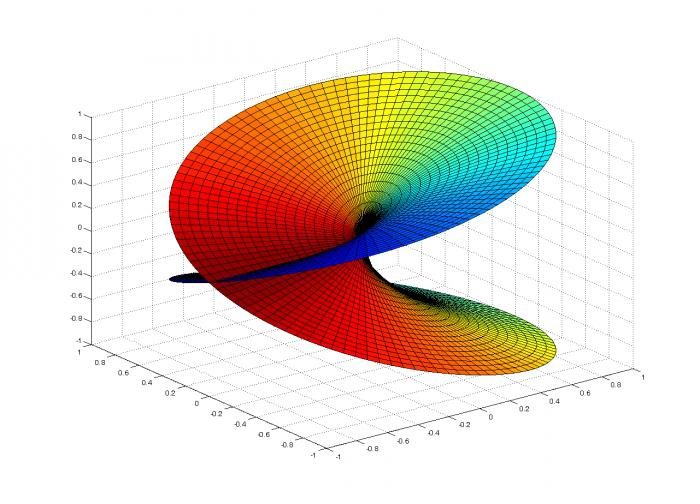Opozoriti je treba, da je na tem področju kvadratni koren zelo povpraševan, saj je del večine geometrijskih formul, potrebnih za izračune. Sam algoritem štetja je precej zapleten in temelji na rekurziji (funkciji, ki kliče sama).

Kvadratni koren v kompleksnem polju C

Na splošno je bil predmet tega članka, ki je spodbudil odprtje polja. kompleksnih števil C, ker matematiki niso bili lahki pri vprašanju pridobitve korena enakomerne stopnje od negativnega števila. Tako se je pojavila imaginarna enota i, za katero je značilna zelo zanimiva lastnost: kvadrat je -1. Zahvaljujoč temu dobimo kvadratne enačbe in negativno diskriminantno rešitev. V C, za kvadratni koren, so pomembne enake lastnosti kot v R, edina stvar je, da so omejitve za radikane odstranjene.