Kako izračunati meje zaporedij?

Matematika je znanost, ki gradi svet. Kot znanstvenik in preprosta oseba - nihče ne more brez tega. Najprej se učijo majhni otroci za štetje, nato seštejejo, odštejejo, množijo in delijo, pri čemer se v srednji šoli pojavijo črkovne oznake, v starejši pa brez njih.

Danes pa se bomo pogovarjali o tem, na čem se gradi vsa znana matematika. Na skupino številk, imenovanih "omejitve zaporedja".

Kaj so sekvence in kje je njihova meja?

Pomen besede "zaporedje" ni težko razlagati. To je konstrukcija stvari, kjer je nekdo ali nekaj urejeno v določenem vrstnem redu ali čakalni vrsti. Na primer, čakalne vrste za vstopnice v živalski vrt - je zaporedje. In to je lahko samo ena! Če, na primer, pogled na čakalno vrsto v trgovini - to je eno zaporedje. In če ena oseba nenadoma zapusti to črto, potem je to še ena vrstica, drugo naročilo.

Beseda "meja" se tudi zlahka razlaga - to je konec nečesa. V matematiki pa so meje zaporedij tiste vrednosti na številski liniji, na katere se nagiba zaporedje števil. Zakaj išče in se ne konča? Vse je preprosto, vrstica s številkami nima konca in večina sekvenc, kot so žarki, ima samo začetek in izgleda takole:

x ₁ , x ₂ , x ₃ , ... x _n ...

Zato je definicija zaporedja funkcija naravnega argumenta. V preprostejših besedah ​​gre za niz članov nekega niza.

Kako je zgrajeno numerično zaporedje?

Najenostavnejši primer numeričnega zaporedja lahko izgleda takole: 1, 2, 3, 4, ... n ...

V večini primerov, za praktične namene, so zaporedja zgrajena iz številk, in vsak naslednji član serije, označen z X, ima svoje ime. Na primer:

x ₁ - prvi član zaporedja;

x ₂ - drugi član zaporedja;

x ₃ - tretji član;

...

x _n je n-ti mandat.

V praktičnih metodah je zaporedje podano s splošno formulo, v kateri je nekaj spremenljivk. Na primer:

X _n = 3n, potem bo sama serija številk izgledala takole:

x ₁ = 3;

x2 = 6;

x3 = 9;

in tako naprej

Ne pozabite, da lahko v splošnem zapisu sekvenc uporabite katera koli latinica, ne samo X. Na primer: y, z, k itd.

Aritmetično napredovanje kot del sekvenc

Preden iščemo meje sekvenc, je priporočljivo globlje potopiti v sam koncept takšnega numeričnega niza, s katerim se je vsakdo srečal v srednjem razredu. Aritmetično napredovanje je niz števil, pri katerih je razlika med sosednjimi člani konstantna.

Naloga: »Naj a ₁ = 15 in korak napredovanja številske serije d = 4. Zgradite prvih 4 članov te serije. "

Rešitev: a ₁ = 15 (po pogojih) - prvi član napredovanja (številske serije).

a ₂ = 15 + 4 = 19 je drugi član napredovanja.

in ₃ = 19 + 4 = 23 - tretji član.

a ₄ = 23 + 4 = 27 je četrti član.

Vendar pa je ta metoda težko doseči velike vrednosti, kot je ₁₂₅ .. Posebej za take primere je bila izvedena formula, primerna za prakso: a _n = a ₁ + d (n - 1). V tem primeru je ₁₂₅ = 15 + 4 (125-1) = 511.

Vrste sekvenc

Večina sekvenc je neskončnih, vredno je spominjati se celo življenje. Obstajata dve zanimivi vrsti številskih serij. Prvi je podan s formulo a _n = (- 1) ⁿ . Matematiki to zaporedje pogosto imenujejo bliskavico. Zakaj? Preverite številčno zaporedje.

-1, 1, -1, 1, -1, 1, itd. S takšnim primerom postane jasno, da lahko številke v zaporedjih zlahka ponovimo.

Faktorsko zaporedje. To je enostavno uganiti - faktorial je prisoten v formuli, ki definira zaporedje. Na primer: a _n = (n + 1)!

Nato bo zaporedje izgledalo takole:

a ₁ = 1x2 = 2;

a2 = 1x2x3 = 6;

a ₃ = 1x2x3x4 = 24 itd.

Zaporedje, ki ga definira aritmetično napredovanje, se imenuje neskončno zmanjšanje, če se za vse člane opazi neenakost -1. n = (–1/2) ⁿ .

a ₁ = - ½;

a ₂ = ¼;

a ₃ = - 1/8 itd.

Obstaja celo zaporedje, ki je sestavljeno iz iste številke. Torej, in _n = 6 je sestavljen iz neskončnega niza šestih.

Določitev omejitve zaporedja

Meje sekvenc so že dolgo obstajale v matematiki. Seveda so si zaslužili svoj kompetentni dizajn. Torej, čas, da se naučite definicije meja sekvenc. Najprej natančno preučite omejitev za linearno funkcijo:

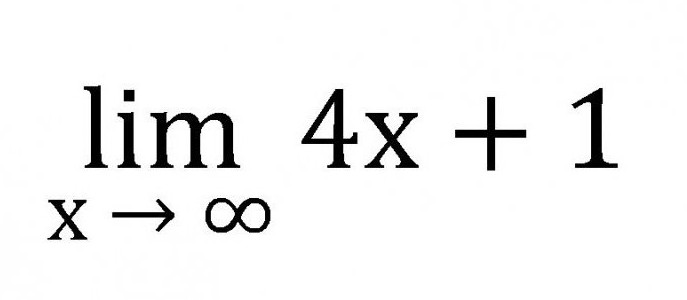
1. Vse omejitve so skrajšane lim.
2. Omejitveni zapis je sestavljen iz okrajšave lim, nekatere spremenljivke težijo k določenemu številu, nič ali neskončnost in tudi iz same funkcije.

Ni težko razumeti, da lahko definicijo meje zaporedja formuliramo takole: gre za določeno število, do katerega se vsi člani sekvence neskončno približujejo. Preprost primer: a _x = 4x ​​+ 1. Potem bo sam zaporedje izgledalo takole.

5, 9, 13, 17, 21 ... x ...

Tako se bo to zaporedje neskončno povečalo, zato je njegova meja enaka neskončnosti pri x → ∞, kar naj bo zapisano tako:

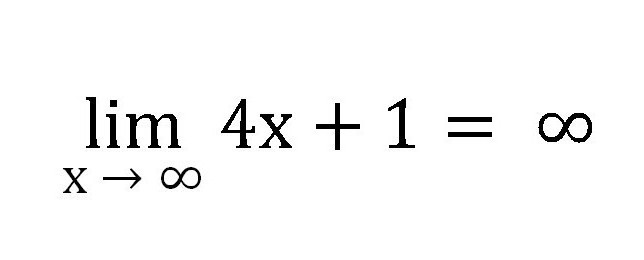
Če vzamemo podobno zaporedje, vendar bo x težil k 1, dobimo:

a _x = 4x ​​+ 1.

Serija številk bo taka: 1.4, 1.8, 4.6, 4.944 in tako naprej. Vsakič, ko je potrebno število nadomestiti bolj in bolj blizu eni (0,1, 0,2, 0,9, 0,986). Iz te serije je jasno, da je meja funkcije pet.

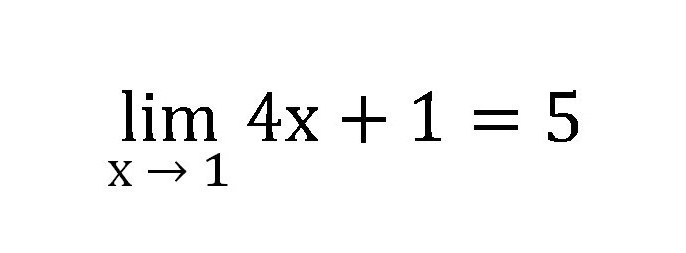
Iz tega dela se je treba spomniti, kaj je meja numeričnega zaporedja, definicija in način reševanja preprostih nalog.

Splošna oznaka omejitve zaporedij

Po pregledu meje numeričnega zaporedja, njegove definicije in primerov lahko nadaljujemo z bolj kompleksno temo. Absolutno lahko vse meje sekvenc formuliramo z eno formulo, ki se običajno analizira v prvem semestru.

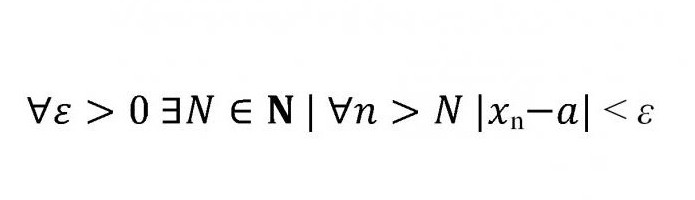
Kaj torej pomeni ta niz črk, modulov in znakov neenakosti?

∀ - količnik univerzalnosti, ki nadomešča besedne zveze »za vse«, »za vse« itd.

∃ - kvantifikator obstoja, v tem primeru pomeni, da je določena vrednost N naravnih števil.

Dolga vertikalna palica, ki sledi N, pomeni, da je dani niz N »tak, da«. V praksi lahko pomeni "tako, da", "tako, da" itd.

Sledi modul. Očitno je, da je modul razdalja, ki po definiciji ni negativna. Torej je modul za razliko strogo manj kot "epsilon".

Za utrditev materiala glasno preberite formulo.

Negotovost in gotovost omejitve

Metoda za določitev meje sekvenc, ki smo jo obravnavali zgoraj, je preprosta v uporabi, vendar v praksi ni tako racionalna. Poskusite najti omejitev za takšno funkcijo:

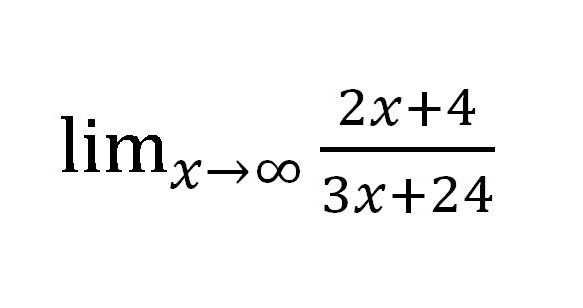
Če nadomestimo različne vrednosti "X" (vsakič povečujemo: 10, 100, 1000, itd.), Potem v števcu dobimo ∞, v imenovalcu pa tudi ∞. Izkazalo se je precej nenavadno: 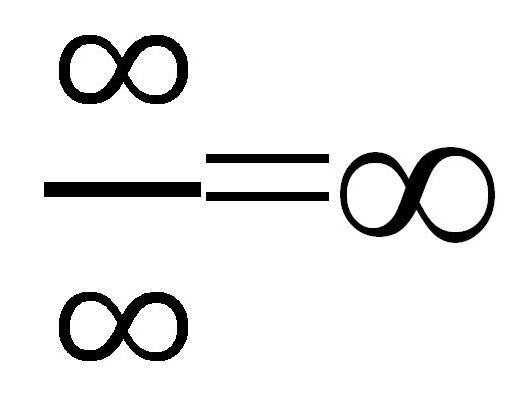Ampak ali je res? Izračunajte mejo numeričnega zaporedja v tem primeru se zdi dokaj enostavno. Možno bi bilo zapustiti vse, kar je, ker je odgovor pripravljen in je bil prejet pod razumnimi pogoji, vendar je za takšne primere drugačen način.

Najprej najdemo najvišjo moč v števcu frakcije - to je 1, ker je x lahko predstavljen kot x ¹ .

Zdaj najdemo najvišjo moč v imenovalcu. Tudi 1.

Števec in imenovalec delimo na spremenljivko na najvišji stopnji. V tem primeru je frakcija deljiva z x ¹ .

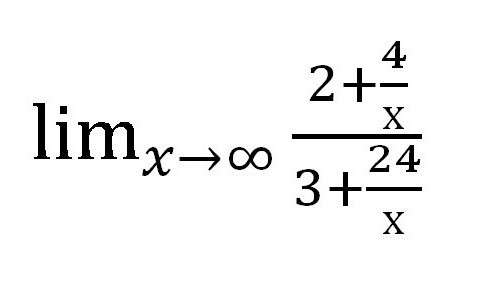
Nato bomo našli, katera vrednost vsakega dodatka, ki vsebuje spremenljivko, teži k. V tem primeru je frakcija. Ko je x → of, vrednost vsake od frakcij teži na nič. Pri izdelavi pisnega dela je vredno izdelati takšne opombe:

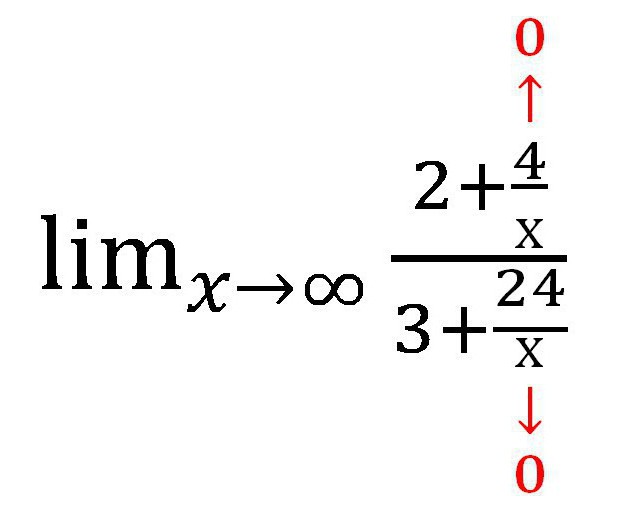
Dobimo naslednji izraz:

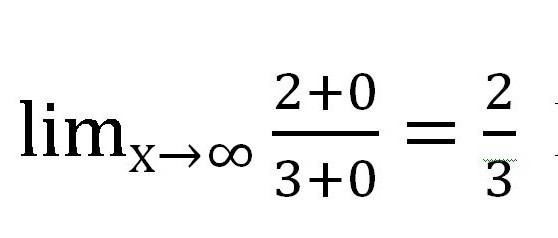
Seveda frakcije, ki vsebujejo x, niso postale ničle! Toda njihova vrednost je tako majhna, da je popolnoma dovoljeno, da je ne upoštevamo pri izračunu. Pravzaprav x v tem primeru ne bo nikoli enak 0, ker ni mogoče razdeliti ničle.

Kaj je soseska?

Recimo, da ima profesor na razpolago zapleteno zaporedje, ki ga očitno dobi z ne manj kompleksno formulo. Profesor je našel odgovor, vendar je primeren? Navsezadnje so vsi ljudje narobe.

Auguste Cauchy je v svojem času prišel na odličen način, da dokaže omejitve sekvenc. Njegovo metodo so imenovali upravljanje soseske.

Recimo, da obstaja točka a, njena soseska v obeh smereh na številski črti je ε ("epsilon"). Ker je zadnja spremenljivka razdalja, je njena vrednost vedno pozitivna.

Sedaj definiramo nekaj zaporedij x _n in predpostavimo, da je deseti izraz zaporedja (x ₁₀ ) vstopi v sosesko. Kako napisati to dejstvo v matematičnem jeziku?

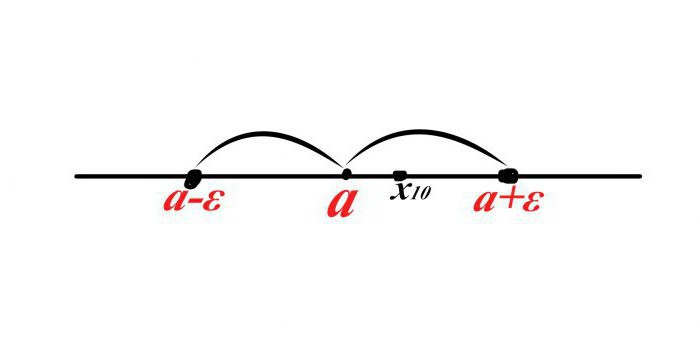
Recimo, da je x ₁₀ desno od točke a, potem je razdalja x ₁₀ –a <ε, če pa postavite »X deseto« na levo od točke a, bo razdalja negativna, toda to je nemogoče, potem dodajte levo stran neenakosti Dobimo | x ₁₀ –a | <ε.

Zdaj je čas, da v praksi pojasnimo to formulo, ki je bila omenjena zgoraj. Določeno število a se upravičeno imenuje končna točka zaporedja, če je za katerokoli mejo zadoščena neenakost ε> 0 in celotna soseska ima svoje naravno število N, tako da bodo vsi člani zaporedja z večjimi številkami znotraj zaporedja | x _n - a | .

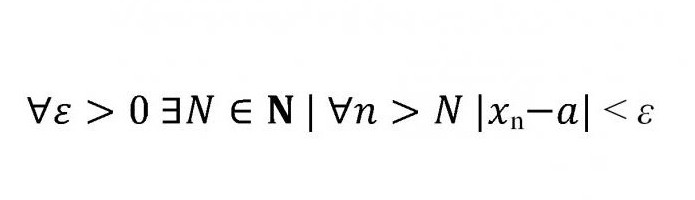
S takšnim znanjem je enostavno uvesti rešitev do meja zaporedja, dokazati ali ovreči pripravljen odgovor.

Teoreme

Teoremi omejitev zaporedja so pomembna sestavina teorije, brez katere je praksa nemogoča. Obstajajo samo štirje glavni izreki, ki se spominjajo, da je včasih mogoče olajšati potek rešitve ali dokazila:

1. Edinstvenost meje zaporedja. Omejitev za vsako zaporedje je lahko le ena ali pa sploh ne. Isti primer s čakalno vrsto, ki lahko ima samo en konec.
2. Če je niz številk omejen, je zaporedje teh številk omejeno.
3. Meja vsote (razlika, produkt) zaporedij je enaka vsoti (razliki, produktu) njihovih omejitev.
4. Meja količnika iz delitve dveh zaporedij je enaka količniku omejitev, če in samo če imenovalec ne izgine.

Dokaz o zaporedjih

Včasih je potrebno rešiti inverzni problem in dokazati dano mejo numeričnega zaporedja. Razmislite na primer.

Dokaži, da je meja zaporedja, ki jo podaja formula, enaka nič.

V skladu z zgoraj omenjenim pravilom mora biti za vsako zaporedje izpolnjena neenakost | x _n - a | <ε. Nadomestite določeno vrednost in referenčno točko. Dobimo:

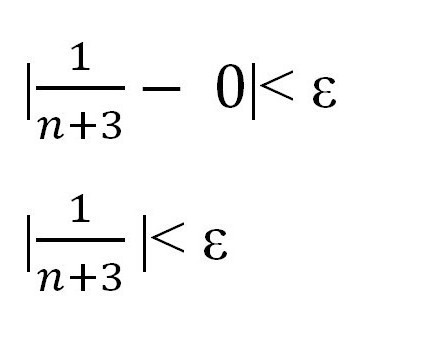
Izrazite n skozi "epsilon", da pokažete obstoj določenega števila in dokažete obstoj omejitvenega zaporedja.

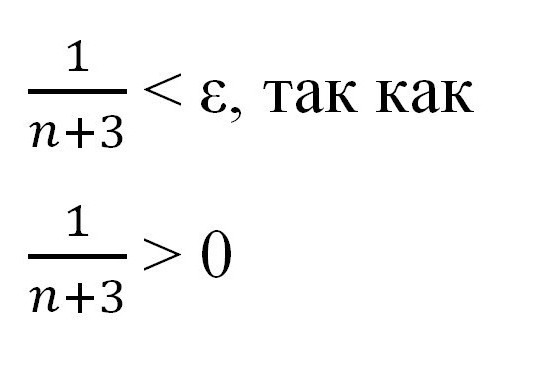
Na tej stopnji je pomembno opozoriti, da sta "epsilon" in "en" pozitivna in neničasta števila. Zdaj lahko nadaljujete z nadaljnjimi transformacijami z uporabo znanja o neenakostih, pridobljenih v srednji šoli.

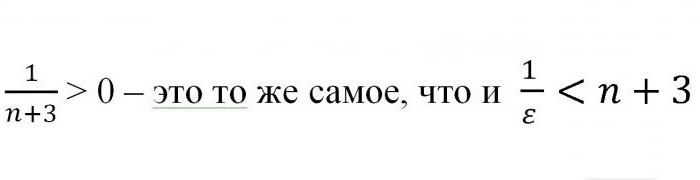
Od tod se izkaže, da je n> –3 + 1 / ε. Ker se je treba spomniti, da govorimo o naravnih številkah, se rezultat lahko zaokroži tako, da ga postavimo v oglate oklepaje. Tako je bilo dokazano, da je za vsako vrednost sosednje »epsilon« točke a = 0 obstajala vrednost, ki drži začetno neenakost. Iz tega lahko varno rečemo, da je število a meja določenega zaporedja. Kar je bilo potrebno dokazati.

S tako priročno metodo lahko dokažemo mejo numeričnega zaporedja, ne glede na to, kako kompleksen je na prvi pogled. Glavna stvar - ne panike ob pogledu na delo.

Ali pa morda ni?

Obstoj omejevalnega zaporedja je v praksi neobvezen. Z lahkoto lahko najdete tako niz številk, ki resnično nimajo konca. Na primer, ista bliskavica x _n = (–1) ⁿ . očitno je, da zaporedje, ki sestoji iz samo dveh številk, ki se ciklično ponavljajo, ne more imeti meje.

Ista zgodovina se ponavlja z zaporedji, ki so sestavljena iz enega števila, delnega, ki ima v času izračunov negotovost poljubnega vrstnega reda (0/0, ∞ / ∞, 0/0, itd.). Vendar se je treba zavedati, da je prišlo tudi do napačnega izračuna. Včasih bo omejitev sekvenc pomagala ponovno preveriti svoje rešitve.

Monotonsko zaporedje

Zgoraj smo obravnavali več primerov zaporedij, metod za njihovo reševanje, zdaj pa bomo poskušali vzeti bolj specifičen primer in ga imenovati »monotono zaporedje«.

Opredelitev: pošteno bi lahko imenovali vsako zaporedje, ki je monotono naraščajoče, če za njo drži strogo neenakost x _n <x _{n +1.} Prav tako se vsako zaporedje pravilno imenuje monotono, če se za to drži neenakost x _n > x _{n +1.}

Poleg teh dveh pogojev obstajajo tudi podobne šibke neenakosti. V skladu s tem je x _n ≤ x _{n + 1} (zaporedje, ki se ne zmanjšuje) in x _n ≥ x _{n +1} (zaporedje, ki se ne povečuje).

Vendar je to lažje razumeti s primeri.

Zaporedje, ki ga podamo s formulo x _n = 2 + n, predstavlja naslednje vrste številk: 4, 5, 6, itd. To je monotono naraščajoča sekvenca.

In če vzamemo x _n = 1 / n, dobimo serijo: 1/3, 1/, 1/5, itd. To je monotono padajoča sekvenca.

Meja konvergentnega in omejenega zaporedja

Omejeno zaporedje - zaporedje, ki ima mejo. Konvergentno zaporedje je niz števil, ki ima neskončno majhno mejo.

Tako je meja omejenega zaporedja veljavna ali kompleksno število. Ne pozabite, da je lahko samo ena omejitev.

Meja konvergentnega zaporedja je neskončno majhna količina (realna ali kompleksna). Če narišete diagram zaporedja, se bo na določeni točki zdelo, da se bo približalo, da se bo obrnilo na določeno vrednost. Zato ime - konvergentno zaporedje.

Monotonska meja

Omejitev za takšno zaporedje je lahko ali pa tudi ne. Sprva je koristno razumeti, kdaj je, od katerega se lahko potisnemo, ko dokažemo odsotnost omejitve.

Med monotonimi zaporedji oddajajo konvergenco in divergirajo. Konvergenca je zaporedje, ki ga tvori množica x in ima realno ali kompleksno mejo v danem nizu. Divergent - zaporedje, ki v svojem nizu nima nobene omejitve (niti realne niti kompleksne).

Poleg tega zaporedje konvergira, če se njegova geometrijska slika konvergira z zgornjo in spodnjo mejo.

Meja konvergenčnega zaporedja je lahko v številnih primerih enaka nič, ker ima vsaka neskončno majhna zaporedje znano mejo (nič).

Ne glede na to, kakšno konvergentno zaporedje, so vsi omejeni, vendar se ne omejijo vsa omejena zaporedja.

Vsota, razlika, produkt dveh konvergentnih sekvenc je tudi konvergentna sekvenca. Vendar je količnik lahko tudi konvergenten, če je definiran!

Različna dejanja z omejitvami

Meje zaporedij so tako pomembne (v večini primerov) kot številke in številke: 1, 2, 15, 24, 362, itd. Izkazalo se je, da se nekatere operacije lahko izvajajo z omejitvami.

Prvič, kot številke in številke, se lahko dodajo in odštejejo omejitve vseh zaporedij. Na podlagi tretjega izreka o mejah zaporedij velja naslednja enakost: meja vsote zaporedij je enaka vsoti njihovih omejitev.

Drugič, na podlagi četrtega izreka o mejah zaporedij velja naslednja enakost: meja produkta n-tega števila zaporedij je enaka zmnožku njihovih omejitev. Enako velja za delitev: meja kvocienta dveh zaporedij je enaka količniku njihovih omejitev, če meja ni nič. Konec koncev, če je meja zaporedja enaka nič, potem dobimo delitev z nič, kar je nemogoče.

Lastnosti zaporedja

Zdi se, da je meja numeričnega zaporedja že podrobno analizirana, vendar so ti stavki, kot so »neskončno majhni« in »neskončno veliki« številki, omenjeni več kot enkrat. Očitno je, če obstaja zaporedje 1 / x, kjer je x → ∞, potem je taka frakcija neskončno majhna in če je zaporedje enako, vendar meja teži na nič (x → 0), potem frakcija postane neskončno velika količina. In takšne količine imajo svoje značilnosti. Lastnosti meje zaporedja, ki imajo majhne ali velike vrednosti, so naslednje:

1. Vsaka količina poljubno majhnih količin bo tudi majhna količina.
2. Vsota vseh velikih količin bo neskončno velika količina.
3. Produkt poljubno majhnih količin je neskončno majhen.
4. Produkt poljubnega števila velikih števil je neskončno velika vrednost.
5. Če je prvotno zaporedje nagnjeno k neskončno velikemu številu, bo količina, ki je nasprotna njej, neskončno majhna in se bo približala ničli.

Dejstvo je, da izračun omejitve zaporedja ni tako težka naloga, če poznate preprost algoritem. Toda meje sekvenc - tema, ki zahteva največ pozornosti in vztrajnosti. Seveda je dovolj samo ujeti bistvo rešitve takih izrazov. Začenši z majhnimi, lahko sčasoma dosežete velike vrhove.