Frakcija - kaj je to? Vrste frakcij

Proučevanje kraljice vseh znanosti - matematike, se na določeni točki sooča z ulomki. Čeprav je ta koncept (kot tudi vrste samih frakcij ali matematične operacije z njimi) precej preprost, ga je treba skrbno obravnavati, saj bo v resničnem življenju zunaj šole zelo koristno. Osvežimo svoje znanje o frakcijah: kaj je to, kaj je, za kaj obstajajo in kako z njimi izvajati različne aritmetične operacije.

Frakcija njenega veličanstva: kaj je to?

Frakcije v matematiki so številke, od katerih je vsaka sestavljena iz enega ali več delov enote. Takšne frakcije se imenujejo tudi navadne ali preproste frakcije. Praviloma so napisana v obliki dveh številk, ki sta ločeni z vodoravno ali poševno črto, se imenuje "delno". Na primer: ½, ¾.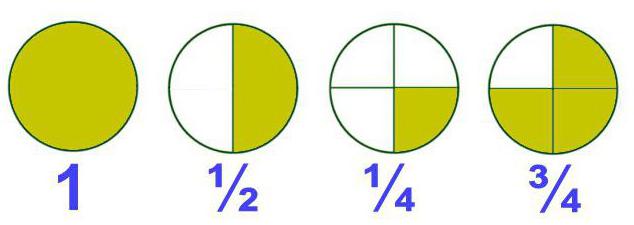

Zgornja ali prva od teh številk je števec (kaže, koliko frakcij se vzame iz števila), spodnji ali drugi pa imenovalec (kaže, koliko enot je razdeljenih v eno).

Fraction bar dejansko opravlja funkcijo oznake delitve. Na primer 7: 9 = 7/9

Tradicionalno so navadne frakcije manj kot ena. Čeprav so decimalke lahko večje od njenih.

Kaj so frakcije za? Da, za vse, ker v resničnem svetu niso vse številke cela števila. Na primer, dve šolarki v jedilnici sta kupili eno slastno čokolado v torbici. Ko so se nameravali deliti sladico, so spoznali dekle in se odločili, da jo bodo zdravili z njo. Vendar pa je zdaj treba pravilno razdeliti čokolado, če upoštevamo, da je sestavljen iz 12 majhnih kvadratov.

Sprva so dekleta želela vse razdeliti enako, nato pa bi vsak dobil štiri kose. Ampak, potem ko so razmislili, so se odločili, da zdravijo dekle, ne 1/3, ampak 1/4 čokolade. In ker šolarke slabo preučujejo frakcije, niso upoštevale, da bi s takšno situacijo imele 9 kosov, ki so zelo slabo razdeljeni na dva dela. Ta precej preprost primer kaže, kako pomembno je, da lahko najdemo pravi del številke. Toda v življenju so takšni primeri veliko več.

Vrste frakcij: navadne in decimalne

Vse matematične frakcije so razdeljene v dve veliki številki: navadni in decimalni. Posebnosti prve izmed njih so bile obravnavane v prejšnjem odstavku, zato je zdaj vredno pozornosti na drugo.

Decimalna točka je pozicijski vnos deleža števila, ki je določen na črki, ločeni z vejicami, brez pomišljaja ali poševnice. Na primer: 0,75, 0,5.

Dejansko je decimalni del enak navadnemu, vendar je v svojem imenovalcu vedno ena ena, ki ji sledijo ničle - od tod tudi njeno ime.

Številka pred vejico je celoštevilni del in vse, kar je po njem, je delno. Vsaka preprosta frakcija se lahko pretvori v decimalno. Tako lahko decimalne frakcije, podane v prejšnjem primeru, zapišemo kot navadne: ¾ in ½.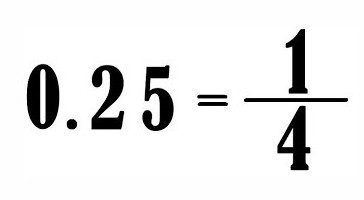

Treba je omeniti, da sta lahko decimalna in navadna frakcija pozitivna in negativna. Če je pred znakom "-", je ta del negativen, če je "+" pozitiven.

Podvrste navadnih frakcij

Takšne vrste frakcij so preproste.

• Pravilno. Imajo vrednost števca vedno manj kot imenovalec. Na primer: 7/8. To je pravilna frakcija, ker je števec 7 manjši od imenovalca 8.
• Napačno. V takih frakcijah sta števca in imenovalec enaka (8/8) ali pa je nižja vrednost manjša od zgornje številke (9/8).
• Mešano To je ime pravilne frakcije, zapisane s celim številom: 8 ½. Razume se kot vsota tega števila in ulomkov. Mimogrede, preprosto lahko naredite, da se na svojem mestu prikaže napačen del. V ta namen mora biti 8 zapisano kot 16/2 + 1/2 = 17/2.
• Spojina. Kot že ime pove, so sestavljeni iz več frakcijskih črt: ½ / ¾.
• Zmanjšano / neuvedljivo. Te lahko vključujejo pravilne in napačne dele. Vse je odvisno od tega, ali lahko števec in imenovalec razdelimo na isto številko. Na primer, 6/9 je zmanjšana frakcija, ker lahko obe komponenti delimo s 3 in dobimo 2/3. Toda 7/9 se nanaša na nevredljivo, saj sta 7 in 9 praštevila, ki nimata skupnega delitelja in ju ni mogoče zmanjšati.

Decimalne številke podvrst

Za razliko od enostavnega decimalnega deleža je razdeljen na samo 2 vrsti.

• Končno - ime je dobilo zaradi dejstva, da ima po vejici omejeno (končno) število števk: 19.25.
• Neskončna frakcija je število z neskončnim številom decimalnih mest. Na primer, če razdelimo 10 na 3, bo rezultat neskončen delež 3,333 ...

Frakcija

Malo težje je izvesti različne aritmetične manipulacije z ulomki kot z navadnimi številkami. Vendar, če ste izvedeli osnovna pravila, rešiti vsak primer z njimi ne bo težko.

Torej, da bi dodali dele med seboj, morate najprej zagotoviti, da imata oba izraza enake imenovalce. Za to je treba najti najmanjše število, ki ga lahko delimo brez ravnotežja imenovalcev dodanih številk.

Na primer: 2/3 + 3/4. Najmanjši skupni večkratnik za njih bo 12, zato mora vsak imenovalec vsebovati to število. Za to se števec in imenovalec prve frakcije pomnožita s 4, izkaže se 8/12, nadaljujemo na enak način z drugim izrazom, toda samo pomnožimo s 3 - 9/12. Zdaj lahko zlahka rešite primer: 8/12 + 9/12 = 17/12. Dobljeni delež je napačna vrednost, ker je števec večji od imenovalca. Lahko in se mora preoblikovati v pravo mešano, deliti 17: 12 = 1 in 5/12.

Če se dodajo mešani ulomki, se najprej izvedejo dejanja s celimi števili in nato z delnimi.

Če je v primeru prisoten decimalni del in pravilen, je potrebno, da sta oba postala preprosta, nato pa ju pripeljite v isti imenovalec in dodate. Na primer, 3,1 + 1/2. Številka 3.1 se lahko napiše kot mešani delež 3 in 1/10 ali kot nepravilna frakcija - 31/10. Skupni imenovalec za dodatke je 10, tako da morate števnik in imenovalec 1/2 izmenično pomnožiti, kar je 5/10. Nato lahko enostavno izračunate vse: 31/10 + 5/10 = 35/10. Dobljeni rezultat je nespremenljiva reducirana frakcija, v normalno obliko jo zmanjšamo za 5: 7/2 = 3 in 1/2 ali decimalno - 3,5.

Če dodate 2 decimalk, Pomembno je, da je decimalna vejica enako število števk. Če temu ni tako, morate dodati potrebno število ničel, ker je v decimalnem primeru to mogoče storiti brez resnih posledic. Na primer, 3,5 + 3,005. Da bi rešili to nalogo, morate na prvo številko dodati dve ničli in nato dodati eno po eno: 3.500 + 3.005 = 3.505.

Odštevanje frakcij

Če odštejemo frakcijo, naredimo enako kot z dodatkom: zmanjšamo na skupni imenovalec, odštejemo en števec od drugega, če je potrebno, rezultat pretvorimo v mešani frakcijo.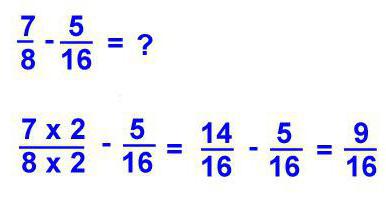

Na primer: 16 / 20-5 / 10. Skupni imenovalec bo 20. Treba je pripeljati drugi del v ta imenovalec, pomnožiti oba dela z 2, izkaže se 10/20. Zdaj lahko rešimo primer: 16 / 20-10 / 20 = 6/20. Vendar se ta rezultat nanaša na zmanjšljive dele, zato je vredno deliti oba dela na 2 in rezultat je 3/10.

Množenje frakcij

Delitev in množenje frakcij sta veliko enostavnejša operacija kot zbiranje in odštevanje. Dejstvo je, da pri izvajanju teh nalog ni treba iskati skupnega imenovalca.

Če želite pomnožiti frakcije, morate izmenično med seboj pomnožiti oba števca in nato oba imenovalca. Rezultat se zmanjša, če je frakcija zmanjšana vrednost.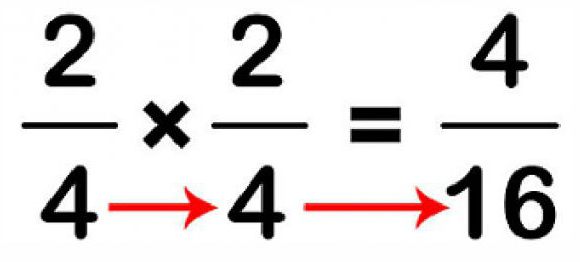

Na primer: 4 / 9x5 / 8. Po nadomestnem množenju dobimo rezultat 4x5 / 9x8 = 20/72. Tak del se zmanjša za 4, tako da je končni odgovor v primeru 5/18.

Kako deliti frakcije

Delitev frakcij je tudi nezapleteno dejanje, v bistvu pa se vseeno zniža na njihovo množenje. Če želite razdeliti en del z drugim, morate obrniti drugo in jo pomnožiti s prvim.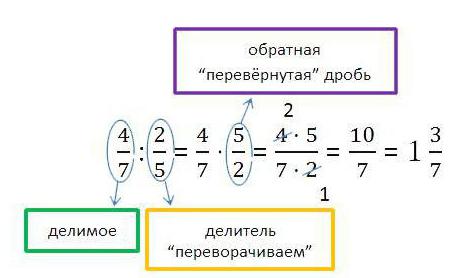

Na primer, delitev frakcij 5/19 in 5/7. Za rešitev primera morate zamenjati imenovalec in števec druge frakcije ter pomnožiti: 5 / 19x7 / 5 = 35/95. Rezultat se lahko zmanjša za 5 - izkaže se 7/19.

V primeru, da je treba delitev razdeliti na praštevilo, je metoda nekoliko drugačna. Sprva je potrebno to številko zapisati kot nepravilen frakcijo in jo nato razdeliti po isti shemi. Na primer, 2/13: 5 naj bo napisano kot 2/13: 5/1. Zdaj morate obrniti 5/1 in množiti dobljeni delež: 2 / 13x1 / 5 = 2/65.

Včasih je potrebno deliti mešanice frakcij. To morajo storiti kot s celimi števili: pretvorite se v napačne frakcije Flip delilnika in pomnožite vse. Na primer, 8 ½: 3. Vse spremenimo v nepravilne frakcije: 17/2: 3/1. Sledi preobrat 3/1 in množenje: 17 / 2x1 / 3 = 17/6. Zdaj je treba napačno frakcijo prevesti v pravilno - 2 celoto in 5/6.

Torej, ko ste razumeli, kaj so frakcije in kako lahko z njimi izvajate različne aritmetične operacije, poskusite ne pozabiti nanj. Navsezadnje so ljudje vedno bolj nagnjeni k temu, da nekaj delijo na dele, kot da bi jih dodali, zato morate biti sposobni narediti prav.