Določanje kotne količine, sile in vztrajnosti. Enačba trenutka Primer reševanja problema

Dinamika vrtenja je eden od pomembnih delov moderne mehanike, ki upošteva zakone rotacijskega gibanja teles okoli osi in točk. V tem članku bomo podrobneje preučili glavno enačbo dinamike vrtenja - enačbo trenutkov.

Trenutek impulzov

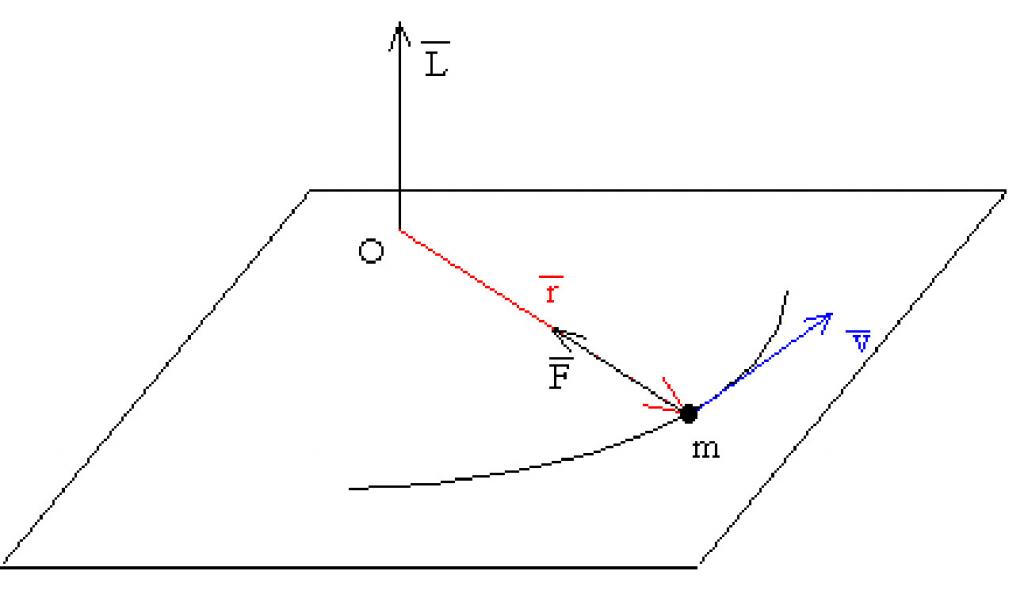
Vsak učenec ve, kaj predstavlja mehanski impulz, ki ga bolj pravilno imenujemo količina gibanja. Predpostavimo, da se materialna točka z maso m vrti okoli O osi z linearno hitrostjo v. Če je polmer rotacije označen kot r, potem lahko napišemo naslednji izraz:

L¯ = [m * v¯ * r¯].

Prva dva dejavnika na desni strani enakosti sta linearni zagon točke. Produkt tega impulza z vektorjem rp, usmerjenim od osi vrtenja do točke, se imenuje kotni moment L¯.

Vrednost Lp je vektor. Usmerjena je pravokotno na ravnino vrtenja točke. Smer vrtilne količine materialne točke se določi z desnim pravilom ali pravilom svinčnika. Z vrtenjem točke v nasprotni smeri urinega kazalca se ustvari pozitivni kotni moment.

Ker je hitrost vrtenja v¯ usmerjena tangencialno na krožno pot, lahko vektorski izraz ponovno napišemo v skalarni obliki:

L = m * v * r.

Trenutek sile

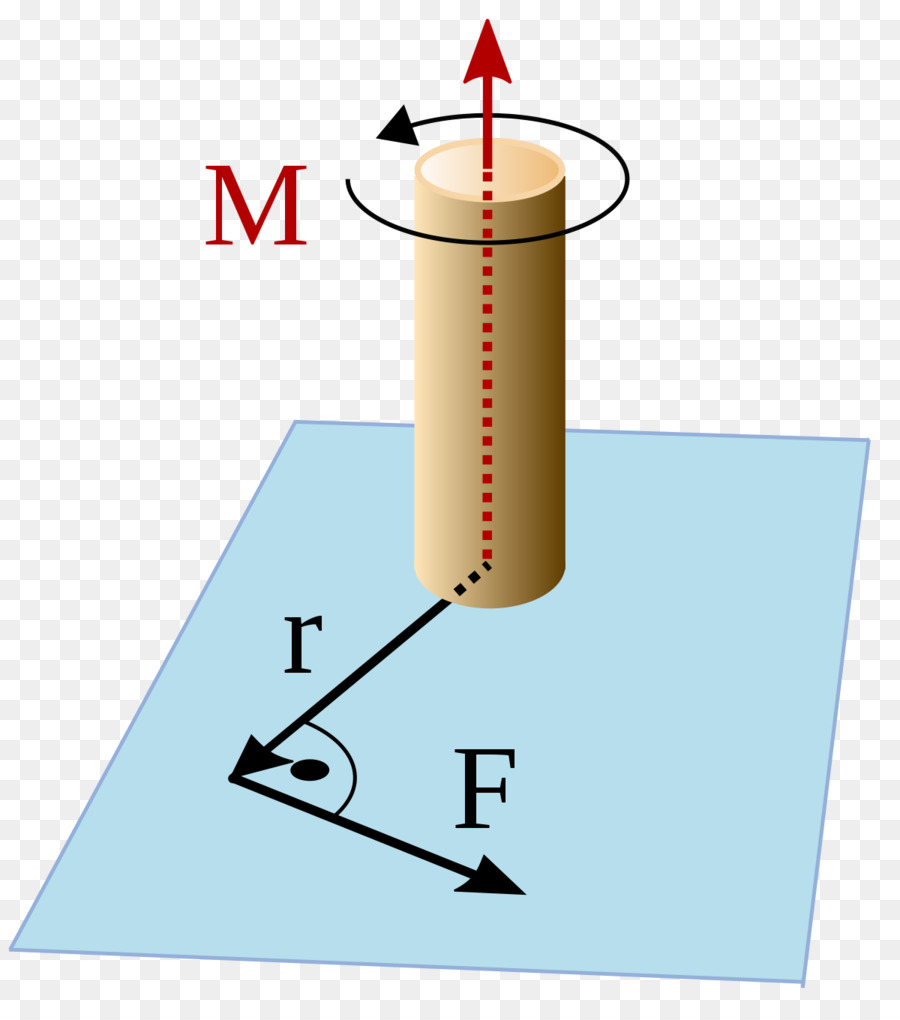
To je še ena pomembna značilnost rotacijskega gibanja. V fiziki se ta količina vnese na enak način kot kot moment momenta materialne točke, toda namesto količine gibanja je treba tangencialno silo nadomestiti z zgornjo formulo. Imamo:

M¯ = [r¯ * F¯].

Trenutek sile, ki se imenuje tudi moment navora, označuje sposobnost slednjega, da izvede obrat sistema in mu da kotni pospešek.

Smer vektorja navora Mp določimo z enakimi pravili kot za vektor L¯. Če sistem izvede pospešeno rotacijo, potem M¯ in L¯ sovpadata v smeri, če se upočasnijo, potem sta nasprotno usmerjena.

Če sta sila F ¯ in radij-vektor r tam medsebojno pravokotni, potem se bo vektorska oblika zapisa spremenila v podoben skalar:

M = r * F.

Vrednost r se imenuje vzvod sile. Večja kot je njena vrednost, večji je trenutek, ko nastane sila F, in večji bo kotni pospešek sistema.

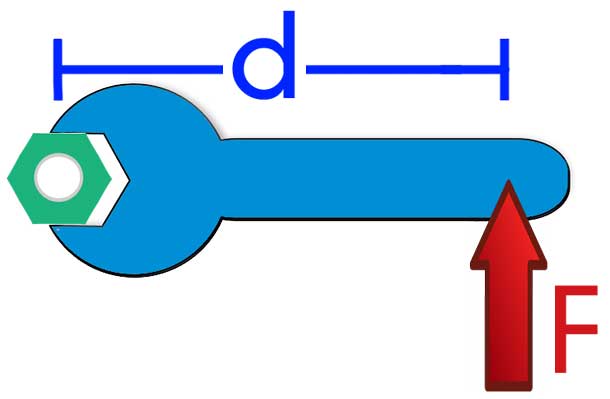
Primeri, ki bi omogočili jasnejšo predstavo o fizičnem pomenu Mpi, odvijajo matico s posebnim dolgim ​​ključem, procesom odpiranja vrat s potiskom blizu ročice in blizu vratnih tečajev, kakor tudi proces držanja telesa določene mase na raztegnjenem in pritisnjenem telesu roko.

Trenutek vztrajnosti

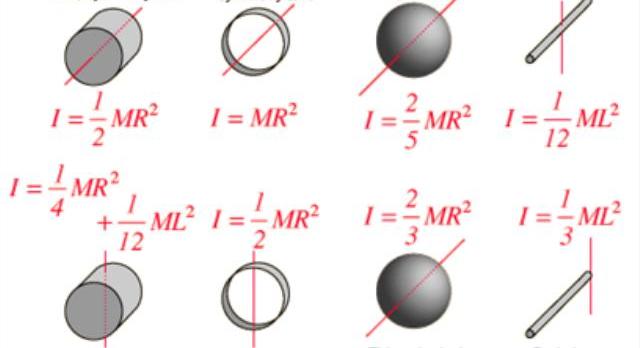
Še vedno je treba opredeliti tretjo točko, ki se uporablja za kvantitativno opisovanje procesa rotacije. Vztrajnostni moment materialne točke, katerega parametri so bili zabeleženi na začetku članka, se izračuna po formuli:

I = m * r ² .

Za razliko od drugih dveh trenutkov (M¯ in L¯) je trenutek vztrajnosti skalar. S pomočjo nje so opisane inercijske lastnosti sistema (analogija z maso med translacijskim gibanjem).

Očitno je, da za določitev vrednosti I za trdno telo z zapleteno obliko in neenakomerno gostoto, uporabite integralno številko:

I = ( _m (r ² * dm).

V bistvu formula odraža seštevanje količin I _i za vsako materialno točko i.

Vztrajnostni moment I je značilen ne le za obliko in porazdelitev mase v sistemu vrtenja, temveč je odvisen tudi od lokacije osi. Mnogi so na primer opazili, da je kovinsko palico ali leseno mop veliko lažje zasukati vzdolž osi, ki poteka skozi njihovo dolžino kot vzdolž pravokotne osi. V drugem primeru je trenutek vztrajnosti bolj pomemben.

Enačba trenutka za materialno točko

Zdaj je čas, da gremo neposredno na temo članka. Če navor M deluje za čas dt, potem to vodi do spremembe momenta momenta za količino dL, ki je:

dL = M * dt.

Ta enakost je diferencialna oblika pisanja enačbe trenutka v fiziki. Prenesite izraz dt na levo stran enakosti in izrecno prepišite dL, dobimo:

dL / dt = M =>

m * dv * r / dt = M.

Spomnimo se, da je linearna hitrost v kinematiki povezana z naslednjo enačbo kota:

v = ω * r.

Če jo nadomestimo z enačbo trenutkov, dobimo:

m * dω * r ² / dt = M =>

I * α = M, kjer je α = dω / dt, I = m * r ² .

Dobljena enakost se pogosto uporablja za določanje kinematičnih značilnosti rotacijskega sistema, če je znan trenutek zunanjih sil M in vztrajnostni moment I.

Zakon ohranjanja vrednosti L

Enačba trenutka kaže, kako se spreminja kotna momentna količina, če deluje zunanji trenutek M. Kaj se bo zgodilo s sistemom, če M izkaže, da je nič? V tem primeru se shrani vrednost L. Matematična formula za to situacijo je napisana takole:

L = const ali

L = m * r * v = m * r ² * ω = I * ω = const.

Upoštevajte, da mora biti pogoj M = 0 izpolnjen samo za zunanje sile. Notranje sile, ki ustvarjajo trenutek M, ne morejo spremeniti trenutka zagona sistema.

Zakon o ohranjanju L se uporablja za rotacijo umetnih satelitov v vesolju in v umetnostnem drsanju. Torej, združuje na različne načine, športnik spremeni vrednost svojega vztrajnostnega momenta, kar vodi do sorazmerne spremembe hitrosti vrtenja.

Primer naloge

Sila 10 N deluje na materialno točko, ki tehta 2 kg, vedoč, da je polmer vrtenja materialne točke okoli osi 0,5 m, in ob upoštevanju, da sila deluje tangencialno na krivuljo, je treba poiskati kotno hitrost točke 5 sekund po začetku gibanja. .

Pišemo enačbo trenutka in izrazimo pospešek α:

I * α = M =>

α = M / I.

Izrazi za M in I sedaj nadomestimo z upoštevanjem pogojev problema, imamo:

α = F * r / (m * r ² ) = F / (m * r).

Ker obravnavano gibanje poteka s konstantnim pospeškom α, je za izračun ω primerna naslednja formula:

ω = α * t.

Če vanj vstavimo dobljeni izraz za α, dobimo končno delovno formulo:

ω = F * t / (m * r).

Glede na podatke problema lahko napišete odgovor: ω = 50 rad / s. Ta vrednost ustreza skoraj 8 polnim obratom okoli osi na sekundo.