Razgradnja kvadratnih trinomal na faktorje: primeri in formule

Razgradnja kvadratnih trimestrov na faktorje se nanaša na šolske naloge, s katerimi se vsi prej ali slej soočajo. Kako to storiti? Kakšna je formula za razgradnjo kvadratnih trinomskih faktorjev? Korak za korakom bomo razumeli s primeri.

Splošna formula

Razgradnja kvadratnih trinomalov na faktorje se izvede z reševanjem kvadratne enačbe. To je preprosta naloga, ki jo je mogoče rešiti z več metodami - poiskati diskriminantno z uporabo Vietovega izreka je tudi grafična rešitev. Prvi dve metodi preučujeta v srednji šoli.

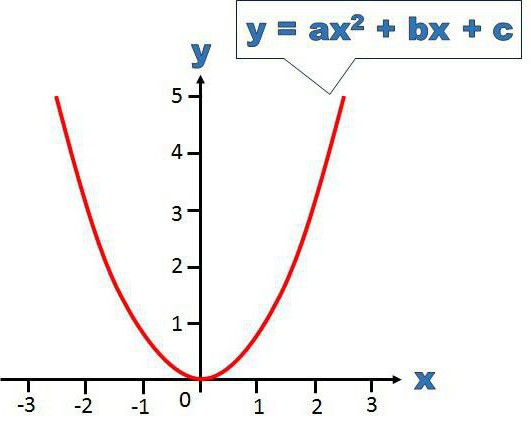
lx ² +kx+n=l(xx ₁ )(xx ₂ ) (1) Splošna formula je naslednja: lx ² + kx + n = l (xx ₁ ) (xx ₂ ) (1)

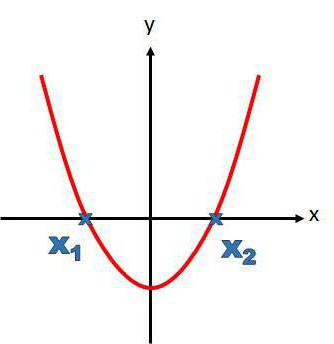
Algoritem izvajanja opravil

Da bi izvedli faktorizacijo kvadratnih trinomialov, morate poznati Vitov izrek, imeti rešitev pri roki, grafično najti rešitev ali poiskati korenine enačbe druge stopnje preko diskriminacijske formule. Če je podan kvadratni trinomij in ga je treba faktorizirati, je zaporedje dejanj naslednje:

1) Izenačite izvirni izraz z ničlo, da dobite enačbo.

2) Navedite takšne pogoje (če obstaja taka potreba).

3) Poiščite korenine na kakršenkoli znan način. Grafična metoda je najbolje uporabiti, če je vnaprej znano, da so korenine cela števila in majhna števila. Ne smemo pozabiti, da je število korenin enako najvišji stopnji enačbe, to je, kvadratna enačba dve koreni.

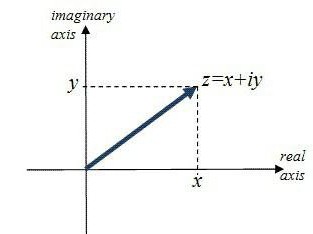
4) V izrazu (1) nadomestite vrednost x .

5) Zapišite razgradnjo kvadratnih trinomskih faktorjev.

Primeri

Na koncu spoznajte, kako se ta naloga izvaja, dovoljuje prakso. Ilustrirajte faktorizacijo kvadratnih trinomskih primerov:

Izraz je treba razširiti:

x ² -17x = -32

Uporabimo naš algoritem:

1) x ² -17x + 32 = 0

2) podobni izrazi se zmanjšajo

3) po formuli Viet je težko najti korenine za ta primer, ker je bolje uporabiti izraz za diskriminantno:

D = 289-128 = 161 = (12,69) ²

x ₁ = 2,155

x2 = 14,845

4) Nadomestimo korenine, ki smo jih našli v osnovni formuli za razgradnjo:

(x-2.155) _* (x-14.845)

5) Nato bo odgovor:

x ² -17x + 32 = (x-2.155) (x-14.845)

Preverite, ali raztopine, ki jih je našel diskriminant, ustrezajo formulam Viet:

2,155 + 14,845 = 17

14,845 ^. 2,155 = 32

Za te korenine je uporabljen Vietov izrek, ki so bili pravilno ugotovljeni, kar pomeni, da je tudi dobljena faktorizacija pravilna.

Podobno razgradimo 12x2 + 7x-6.

12x2 + 7x-6 = 0

D = 337

x ₁ = -7 + (337) ^1/2

x ₂ = -7- (337) ^1/2

V prejšnjem primeru so bile rešitve neznane številke, toda realne številke, ki jih je enostavno najti, pred vami je kalkulator. Zdaj razmislite o bolj zapletenem primeru, v katerem bodo korenine kompleksne: faktoring x ² + 4x + 9. Po formuli za Vieto korenine ni mogoče najti, diskriminant pa je negativen. Korenine bodo na kompleksni ravnini.

D = -20

Izhajajoč iz tega dobimo zanimive korenine -4 + 2i * 5 ^1/2 in -4-2i _* 5 ^1/2 , ker (-20) ^1/2 = 2i * 5 ^1/2 .

Dobimo želeno razgradnjo in nadomestimo korenine v splošni formuli.

Drug primer: izraz 23x ² -14x + 7 je treba upoštevati.

=0 Imamo enačbo 23x2 -14x + 7 = 0

D = -448

To pomeni, da so korenine 14 + 21,166i in 14-21,166i. Odgovor bo:

23x2 -14x + 7 = 23 (x-14-21,166i) * (x-14 + 21,166i).

Dajmo primer, ki ga je mogoče rešiti brez pomoči diskriminantne osebe.

Recimo, da morate razširiti kvadratno enačbo x 2 -32x + 255. Očitno je mogoče rešiti z diskriminantno, v tem primeru pa je hitreje pobrati korenine.

x 1 = 15

x 2 = 17

Torej x2 -32x + 255 = (x-15) (x-17).