Vse možnosti, kako najti trapezoidno področje
Večstranski trapez ... Lahko je poljuben, enakokraren ali pravokoten. V vsakem primeru pa morate vedeti, kako najti območje trapeza. Seveda, najlažji način, da se spomnimo osnovnih formul. Včasih pa je lažje uporabiti tisto, ki je izpeljana z vsemi značilnostmi določenega geometrijska oblika.
Nekaj besed o trapezu in njegovih elementih
Vsak štirikotnik, katerega dve strani sta vzporedni, se lahko imenuje trapez. Na splošno niso enake in se imenujejo baze. Večji med njimi je nižji, drugi pa zgornji.
Drugi dve strani sta stranski. Za poljuben trapezoid imajo različne dolžine. Če so enaki, postane številka enakokračna.
Če je kot med obema stranema in bazo nenadoma 90 stopinj, je trapez pravokoten.
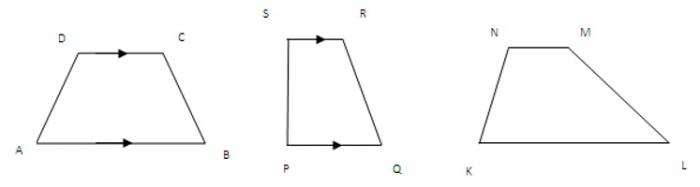
Vse te lastnosti lahko pomagajo pri reševanju problema, kako najti območje trapeza.
Med elementi številke, ki so lahko nepogrešljivi pri reševanju problemov, lahko poudarimo naslednje:
- višina, to je segment, pravokoten na obe osnovi;
- srednja črta, ki ima s konci sredi strani.
S kakšno formulo za izračun površine, če poznate osnovo in višino?
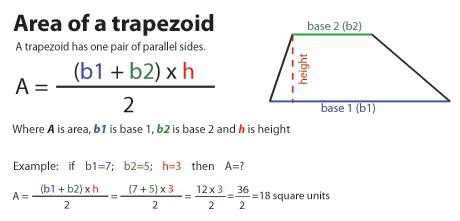
Ta izraz poda glavni zavezanec, ker lahko te vrednosti najpogosteje prepoznate, tudi če niso podane izrecno. Torej, razumeti, kako najti trapezno območje morate zložiti obe osnovi in jih razdeliti na dva dela. Dobljena vrednost se nato pomnoži z vrednostjo višine.
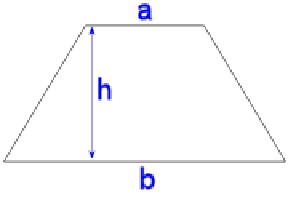
Če osnove označimo s črkama a 1 in a 2 , je višina n, potem bo formula za to območje izgledala takole:
S = ((a 1 + a 2 ) / 2) * n.
Formula za izračun površine, če je podana njena višina in srednja črta
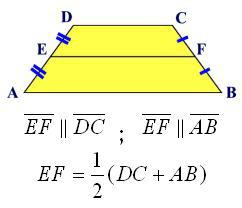
Če ste pozorni na prejšnjo formulo, je enostavno videti, da je vrednost srednje črte v njej očitno prisotna. Sama vsota baz, deljena z dvema. Naj bo srednja črta označena s črko l, potem bo formula za to območje taka:
Ad
S = l * n.
Sposobnost, da najdemo območje diagonalno
Ta metoda bo pomagala, če poznate kot, ki ga oblikujejo. Predpostavimo, da so diagonale označene s črkami q 1 in g 2 , koti med njimi pa so α in β. Potem bo formula, kako najti območje trapeza, napisana takole:
S = ((d 1 * d 2 ) / 2) * sin α.
V tem izrazu lahko enostavno nadomestite α z β. Rezultat se ne bo spremenil.
Kako ugotoviti območje, če so znane vse strani slike?
Obstajajo tudi situacije, ko so na tej sliki znane ravno tiste strani. Ta formula je okorna in težko si jo je zapomniti. Ampak to je mogoče. Naj bodo strani označene: v 1 in 2 , osnova in 1 več kot 2 . Nato bo formula za območje izgledala takole:
Ad
S = ((a 1 + a 2 ) / 2) * √ {v 1 2 - [(a 1 - a 2 ) 2 + v 1 2 - v 2 2 ) / (2 * (a 1 - a 2 )) ] 2 }.
Načini za izračun površine enakokrakega trapeza
Prvo je povezano z dejstvom, da je v njej mogoče vnesti krog. In, vedoč njegov polmer (je označen s črko r), kot tudi kot na bazi - γ, lahko uporabite naslednjo formulo:
S = (4 * r 2 ) / sin γ.
Slednja splošna formula, ki temelji na poznavanju vseh strani slike, bo bistveno poenostavljena, ker imajo strani enak pomen:
S = ((a 1 + a 2 ) / 2) * √ {v 2 - [(a 1 - a 2 ) 2 / (2 * (a 1 - a 2 ))] 2 }.
Metode za izračun površine pravokotnega trapeza
Jasno je, da bo naredil kateri koli izmed naštetih za poljubno obliko. Ampak včasih je koristno vedeti za eno značilnost takega trapeza. Leži v tem, da je razlika v kvadratih dolžin diagonal enaka razliki, sestavljeni iz kvadratov baz.
Ad
Pogosto so formule za trapez pozabljene, izrazi za področja pravokotnika in trikotnika pa se zapomnijo. Potem lahko uporabite preprost način. Razdelite trapez na dve obliki, če je pravokotna ali tri. Ena natanko bo pravokotnik, drugi ali dva preostala trikotnika. Po izračunu območij teh številk jih bomo le dodali.
To je dokaj preprost način kako najti kvadrat trapez.
Kaj če so znane koordinate tock trapeza?
V tem primeru boste morali uporabiti izraz, ki vam omogoča, da določite razdaljo med točkami. Uporablja se lahko trikrat: za učenje obeh podlag in ene višine. Nato uporabite prvo formulo, ki je opisana nekoliko višje.
Za ponazoritev te metode lahko navedete primer. Glede na tocke s koordinatama A (5; 7), B (8; 7), C (10; 1), D (1; 1). Potrebno je poznati območje slike.
Preden najdete območje trapeza, morate izračunati osnovne dolžine s koordinatami. Potrebovali boste naslednjo formulo:
dolžina segmenta = √ {(razlika prvih koordinat točk) 2 + (razlika drugih koordinat točk) 2 }.
Zgornja baza je označena z AB, kar pomeni, da bo njena dolžina enaka √ {(8-5) 2 + (7-7) 2 } = =9 = 3. Spodnja bo SD = √ {(10-1) 2 + (1-1) ) 2 } = =81 = 9.
Sedaj morate imeti višino od vrha do baze. Naj bo njegov začetek v točki A. Konec segmenta bo na spodnji bazi v točki s koordinatami (5; 1), naj bo točka N. Dolžina segmenta AN bo enaka √ {(5-5) 2 + (7-1) 2 } = =36 = 6.
Ad
Preostale vrednosti je treba nadomestiti s formulo trapezoidne površine:
S = ((3 + 9) / 2) * 6 = 36.
Problem je rešen brez enot, ker koordinatna mreža ni določena. Lahko je milimeter ali meter.
Primeri nalog
1. Pogoj. Znan kot med diagonalami poljubnega trapeza je enak 30 stopinj. Manjša diagonala je 3 dm, druga pa 2-krat večja. Potrebno je izračunati površino trapeza.
Odločitev. Najprej morate vedeti dolžino druge diagonale, ker brez tega ne morete prešteti odgovora. Izračunajte ga enostavno, 3 * 2 = 6 (dm).
Zdaj morate uporabiti ustrezno formulo za območje:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (dm 2 ). Problem rešen.
Odgovor: površina trapeza je 4,5 dm 2 .
2. Pogoj. V trapezu AVSD so osnove AD in BC segmenti. Točka E je sredina strani SD. Iz nje, pravokotno na ravno črto AB, je narisan konec tega segmenta s črko N. Znano je, da so dolžine AB in EH 5 in 4 cm, zato je potrebno izračunati površino trapeza.
Ad
Odločitev. Najprej morate narediti risbo. Ker je vrednost pravokotnice manjša od strani, na katero je vodena, bo trapez nekoliko podaljšan navzgor. Torej bo EN znotraj številke.
Da bi jasno videli napredek naloge, boste morali izvesti dodatno gradnjo. Namreč, narišite ravno črto, ki bo vzporedna stranici AB. Točke presečišča te črte z AD - P in nadaljevanjem oboroženih sil - X. Rezultat je paralelogram. Poleg tega je njegovo območje enako želenemu. To je posledica dejstva, da so trikotniki, ki so se pojavili z dodatno konstrukcijo, enaki. To izhaja iz enakosti strani in dveh vogalov, ki ležijo ob njem, enega - navpično, drugega - ležečega prečno.
Poiskati območje paralelograma je mogoče s formulo, ki vsebuje izdelek strani in višino, ki je na njej spuščena.
Tako je površina trapeza 5 * 4 = 20 cm2.
Odgovor: S = 20 cm 2 .
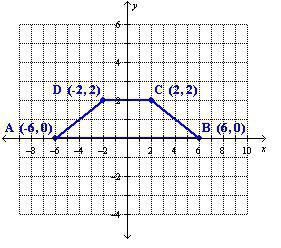
3. Stanje. Elementi enakokrakega trapeza imajo naslednje pomene: spodnja podlaga je 14 cm, zgornja je 4 cm, akutni kot 45 °. Potrebno je izračunati njegovo območje.
Odločitev. Naj bo manjša baza označena kot BC. Višina iz točke B se imenuje HV. Ker je kot 45 °, bo trikotnik ABH pravokoten in enakokrajen. Torej, AN = BH. Poleg tega je NA zelo enostavno najti. Je enaka polovici osnovne razlike. To je (14 - 4) / 2 = 10/2 = 5 (cm).
Razlogi so znani, višina štetja. Uporabite lahko prvo formulo, ki je bila tukaj upoštevana za poljuben trapez.
S = ((14 + 4) / 2) * 5 = 18/2 x 5 = 9 x 5 = 45 (cm2).
Odgovor: Zahtevana površina je 45 cm 2 .
Št. 4. Stanje. Obstaja poljuben trapezoidni AVSD. Na njegovih straneh se vzamejo točke O in E, tako da je OE vzporedno z dnom skrinje. Območje trapeza AOED je petkrat večje od območja CFE. Izračunajte OE vrednost, če so osnovne dolžine znane.
Odločitev. Potrebno bo narisati dve vzporedni AB premici: prva skozi točko C, njeno presečišče z OE je točka T; drugi skozi E in sečišče z AD bo M.
Naj neznana OE = x. Višina manjšega trapeza CFE je n 1 ;
Ker so področja teh dveh trapezov povezana kot 1 do 5, lahko zapišemo naslednjo enakost:
(x + a 2 ) * n 1 = 1/5 (x + a 1 ) * n 2
ali
n 1 / n 2 = (x + a 1 ) / (5 (x + a 2 )).
Višine in stranice trikotnikov so sorazmerne po konstrukciji. Zato lahko napišemo drugo enakost:
n 1 / n 2 = (x - a 2 ) / (a 1 - x).
V zadnjih dveh vnosih na levi strani so enake vrednosti, tako da lahko napišemo, da je (x + a 1 ) / (5 (x + a 2 )) enako (x - a 2 ) / (a 1 - x).
To zahteva vrsto sprememb. Najprej pomnožite prečno. Pojavijo se oklepaji, ki označujejo razliko v kvadratih in po uporabi te formule dobite kratko enačbo.
Treba je odpreti oklepaje in premakniti vse izraze iz neznanega "x" na levo stran in nato izvleči kvadratni koren.
Odgovor : x = √ {(a 1 2 + 5 a 2 2 ) / 6}.