Kaj je integral? Integrali s podrobno rešitvijo. Integralna tabela
Beseda "integral" izhaja iz latinske integralis - holistične. Ta naslov je predlagan v 17. stoletju. študent velikega Leibniza (in tudi izjemnega matematika) I. Bernoullija. In kaj je integral v modernem smislu? V nadaljevanju bomo skušali podati celovit odgovor na to vprašanje.
Zgodovinsko ozadje koncepta integral
V začetku 17. stoletja pri vodilnih znanstvenikih je obstajalo veliko število fizičnih (predvsem mehanskih) nalog, pri katerih je bilo treba raziskati odvisnosti nekaterih količin od drugih. Najočitnejši in najbolj pereči problemi so bili določitev trenutne hitrosti neenakomernega gibanja telesa v danem trenutku in njena obratna težava pri iskanju velikosti poti, ki jo je telo v tem času premikalo v določenem časovnem obdobju. Danes že vemo, kaj je integral hitrosti gibanja - to je pot, ki jo potuje. Toda razumevanje, kako ga izračunati, poznavanje hitrosti v vsakem trenutku, se ni pojavilo takoj.
Najprej se je pri obravnavi takšnih odvisnosti fizikalnih veličin, na primer poti na hitrost, oblikovala matematična zasnova funkcije y = f (x). Proučevanje lastnosti različnih funkcij je pripeljalo do nastanka. T matematična analiza. Znanstveniki aktivno iščejo načine za preučevanje lastnosti različnih funkcij. 
Kako je izračun integralov in derivatov?
Ko je Descartes ustvaril osnove analitične geometrije in priložnost za grafično prikazovanje funkcionalnih odvisnosti v osi kartezičnega koordinatnega sistema, so se raziskovalci soočili z dvema večjima novima nalogama: kako na vsaki točki potegniti tangento na ukrivljeno črto in kako najti območje številke, ki je omejena nad to krivuljo in ravne črte, vzporedno z koordinatnimi osmi. Na nepričakovan način se je izkazalo, da je prvi enakovreden iskanju trenutne hitrosti, drugi pa iskanju prevožene razdalje. Navsezadnje je bila v primeru neenakomernega gibanja upodobljena v kartezičnih oseh koordinatnih »razdalj« in »časa« z določeno ukrivljeno črto.
Genius Leibniz in Newton sredi 17. stoletja. ustvarjene so bile metode, ki omogočajo reševanje obeh problemov. Izkazalo se je, da je za izvedbo tangente na krivuljo na točki potrebno poiskati vrednost tako imenovanega derivata funkcije, ki opisuje to krivuljo na zadevni točki, ta vrednost pa je enaka hitrosti spremembe funkcije, to je glede na odvisnost od poti proti hitrosti. trenutna hitrost telesa.
Da bi našli območje, ki ga omejuje krivulja, je bilo treba izračunati določen integral, ki je dal njegovo točno vrednost. Derivativni in integralni - osnovni pojmi diferencialnega in integralnega računa, ki so osnova sodobne matematične analize - najpomembnejši del višje matematike.
Površina pod krivuljo
Torej, kako ga definirati natančna vrednost? Poskusimo podrobno razkriti proces njegovega izračuna preko integrala od samega začetka.
Naj bo f kontinuirana funkcija v intervalu [ab]. Upoštevajte krivuljo y = f (x), prikazano na spodnji sliki. Kako najti območje, ki ga omejuje krivulja, os x in črte x = a in x = b? To je območje zasenčene slike na sliki. 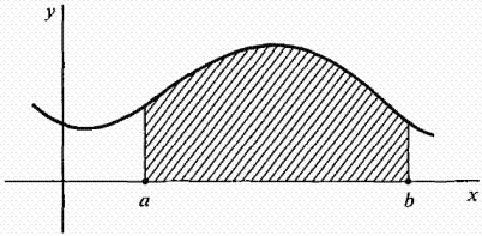
Najenostavnejši primer je, ko je f stalna funkcija; to pomeni, da je krivulja vodoravna črta f (X) = k, kjer je k konstanta in k ≥ 0, kot je prikazano na spodnji sliki. 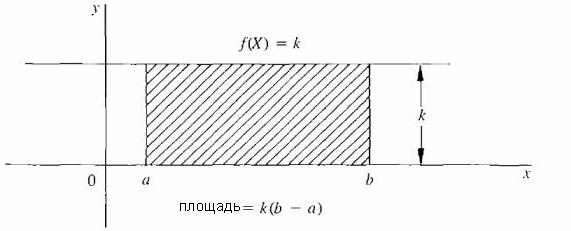 V tem primeru je območje pod krivuljo samo pravokotnik z višino k in širino (b - a), zato je območje definirano kot: k · (b - a).
V tem primeru je območje pod krivuljo samo pravokotnik z višino k in širino (b - a), zato je območje definirano kot: k · (b - a).
Območja nekaterih drugih enostavnih oblik, kot so trikotnik, trapez in polkrog, so podane po planimetričnih formulah.
Območje pod katerokoli kontinuirano krivuljo y = f (x) je podano z določenim integralom, ki je zapisan na enak način kot običajen integral.
Riemannova vsota
Preden se potopimo v podroben odgovor na vprašanje, kaj je integral, poudarimo nekaj osnovnih idej.
Najprej je območje pod krivuljo razdeljeno na določeno število n navpičnih črt z dovolj majhno širino Δx. Nadalje je vsak navpični trak nadomeščen z navpičnim pravokotnikom višine f (x), širine Δx in površine f (x) dx. Naslednji korak je oblikovanje vsote območij vseh teh pravokotnikov, ki se imenujejo Riemannova vsota (glej spodnje slike).
Z risanjem naših lesx širokih pravokotnikov lahko vzamemo njihovo višino, ki je enaka vrednosti funkcije na levem robu vsakega traku, kar pomeni, da bo krivulja skrajne leve točke njihovih zgornjih kratkih strani Δx široke. Hkrati so v odseku, kjer funkcija raste in je njena krivulja konveksna, vsi pravokotniki pod to krivuljo, tj. Njihova vsota bo zagotovo manjša od točne vrednosti območja pod krivuljo na tem območju (glej sliko spodaj). Ta metoda približevanja se imenuje levo. 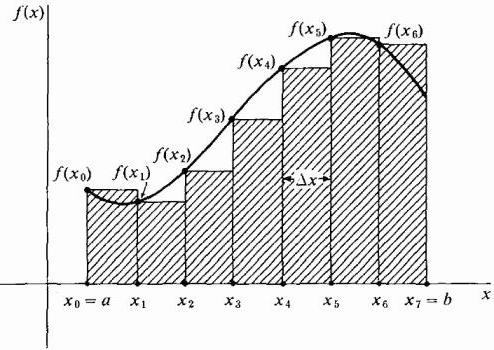
Načeloma je mogoče približati pravokotnike tako, da so skrajne desne točke njihovih zgornjih kratkih strani širine Δx na krivulji. Nato bodo višje od krivulje in približek območja v tem območju bo večji od njegove točne vrednosti, kot je prikazano na spodnji sliki. Ta metoda se imenuje pravica. 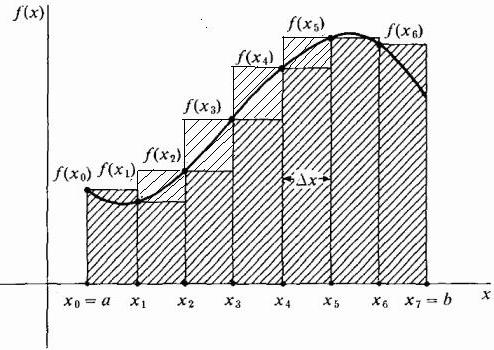
Lahko pa tudi vzamemo višino vsakega od približnih pravokotnikov, ki je enaka le neki vrednosti funkcije na poljubni točki x * i znotraj ustreznega traku Δx i (glejte sl. spodaj). V tem primeru lahko celo ne vzamemo enake širine vseh trakov. 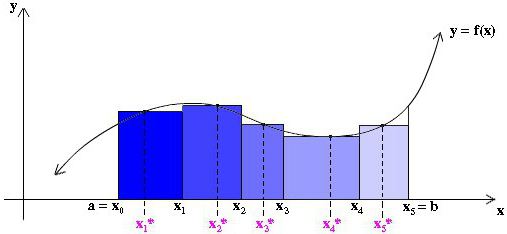
Znesek Riemann naredimo:

Prehod iz Riemannove vsote v določen integral
V višji matematiki je dokazan izrek, ki navaja, da če je z neomejenim povečanjem števila n približnih pravokotnikov njihova največja širina nagnjena k nič, potem se Riemannova vsota A n nagiba k neki meji A. Število A je enako za katerokoli metodo za oblikovanje približnih pravokotnikov in za vsako izbiro točk x * i .
Jasna razlaga izreka je podana na spodnji sliki.
To kaže, da je, če so ožji pravokotniki, bližje območje stopničaste figure območju pod krivuljo. Ko je število pravokotnikov n → ∞, je njihova širina Δx i → 0, meja A vsote A n pa je numerično enaka zahtevanemu območju. Ta omejitev in obstaja določen integral funkcije f (x): 
Integralni simbol, ki je modificiran italic S, je predstavil Leibniz. J. B. Fourier je predlagal, da je zapis za integral na vrhu in na dnu. Istočasno so jasno označene začetne in končne vrednosti x.
Geometrijska in mehanska interpretacija določenega integrala
Poskusimo podrobno odgovoriti na vprašanje, kaj je integral? Razmislite o integralu na intervalu [a, b] pozitivne funkcije f (x) v njem in predpostavite, da je zgornja meja večja od spodnje. Če so ordinate funkcije f (x) negativne v notranjosti [a, b], potem je absolutna vrednost integrala enaka površini med osjo x in grafikonom y = f (x), sam integral je negativen. V primeru enega ali večkratnih presečišč osi y = f (x) abscise na odseku [a, b], kot je prikazano na spodnji sliki, je za izračun integrala treba določiti razliko, pri kateri je zmanjšanje enako skupni površini ploskev nad osjo x , in odbitni - skupna površina površin pod njo. Mehanska interpretacija določenega integrala je tesno povezana z geometrijskim. Vrnimo se na odsek »Riemannova vsota« in si predstavljamo, da graf, prikazan na slikah, izraža funkcijo hitrosti v = f (t) z neenotnim gibanjem materialne točke (os osi je časovna os). Potem bo območje vsakega približnega pravokotnika širine Δt, ki smo ga zgradili med nastajanjem Riemannove vsote, izrazilo približno pot točke v času Δt, in sicer v (t *) Δt. Skupna vsota površin pravokotnikov na intervalu od t 1 = a do t 2 = b izraža približno pot s v času t 2 - t 1 in njena meja, tj. integral (definiran) od a do b funkcije v = f (t) nad dt bo dala natančno vrednost poti s. Če se vrnemo k njeni oznaki, lahko dobro predpostavimo, da je a = const in b specifična vrednost neke neodvisne spremenljivke x. Nato se določen integral z zgornjo mejo x̃ iz konkretnega števila spremeni v funkcijo x̃. Takšen integral je enak površini slike pod krivuljo, ki jo na spodnji sliki označujejo točke aABb. Recimo, da smo dali spremenljivko x̃ = b nekaj majhnega prirastka Δx̃. Nato prirastek površine slike aABb sestoji iz območja pravokotnika (zasenčenega na sliki) Bb ̃ Δx̃ in območja podatek BDC pod krivuljo. Površina pravokotnika je enaka Bb x Δx f = f (x̃) Δx̃, kar pomeni, da je linearna funkcija prirastka neodvisne spremenljivke. Območje oblike BDC je očitno manjše od površine pravokotnika BDCK = Δx̃ ∙ Δy, in ker je Δx̃ → 0 težnja, se zmanjša še hitreje kot to. Zato je f (x̃) Δx̃ = f (x̃) dx̃ diferencial spremenljivega območja aABb, tj. Diferencial definiranega integrala Iz tega lahko sklepamo, da je izračun integralov sestavljen iz iskanja funkcij iz danih izrazov njihovih diferencialov. Integralni račun je prav sistem metod za iskanje takšnih funkcij iz njihovih znanih diferencialov. Povezuje odnos med diferenciacijo in integracijo in kaže, da obstaja operacija, ki je obratno odvisna od diferenciacije funkcije - njene integracije. Prav tako kaže, da če je katera koli funkcija f (x) neprekinjena, potem lahko z uporabo te matematične operacije v njej najdemo celotno skupino (množico, množico) funkcij, ki so za njo primitivne (ali kako drugače, najdemo nedoločen integral iz nje). Naj bo funkcija F (x) oznaka rezultata integracije funkcije f (x). Ujemanje med tema dvema funkcijama kot rezultat integracije drugega od njih je navedeno tako: Kot je razvidno, integralni simbol ne predstavlja meja integracije. To pomeni, da se iz določenega preoblikuje v nedoločen integral. Beseda "nedoločen" pomeni, da rezultat integracijske operacije v tem primeru ni ena, ampak številne funkcije. Poleg funkcije F (x) sama katera koli funkcija F (x) + C zadostuje zadnjim izrazom, kjer je C = const. To pomeni, da se lahko stalni član v skupščini antivojnih izdelkov določi poljubno. Poudariti je treba, da če je integral, ki ga definira funkcija, število, potem je nedoločen funkcija, natančneje, njihova množica. Izraz "integracija" se uporablja za definiranje iskanja obeh vrst integralov. Je popolno nasprotje ustreznega pravila za diferenciacijo. Kako se upoštevajo nedoločeni integrali? Primeri tega postopka upoštevamo posebne funkcije. Poglejmo funkcijo moči splošne oblike: f (x) = cx n Ko smo to naredili z vsakim izrazom v izrazu integrabilne funkcije (če jih je več), na koncu dodamo konstanto. Spomnimo se, da ga jemanje derivata konstantne vrednosti uniči, tako da bomo z integracijo katerekoli funkcije dobili obnovitev te konstante. Označujemo ga s C, ker je konstanta neznana - lahko je poljubna številka! Zato lahko imamo neskončno veliko izrazov za nedoločen integral. Oglejmo si enostavne nedoločene integrale, primeri katerih so prikazani spodaj. Recimo, da morate poiskati integral funkcije: f (x) = 4x 2 + 2x - 3. Začnimo s prvim terminom. Pogledamo eksponent 2 in ga povečamo za 1, nato pa prvič delimo z dobljenim kazalnikom 3. Dobimo: 4 (x 3 ) / 3. Potem pogledamo naslednjega člana in naredimo isto. Ker ima eksponent 1, bo dobljeni kazalnik 2. Tako ga delimo z 2: 2 (x 2 ) / 2 = x 2 . Zadnji izraz ima faktor x, vendar ga ne vidimo. Zadnji izraz lahko predstavljamo kot (-3x 0 ). To je enakovredno (-3) ∙ (1). Če uporabimo pravilo integracije, indikatorju dodamo 1, da ga dvignemo na prvo stopnjo, potem pa zadnji del razdelimo na 1. Dobimo 3x. To integracijsko pravilo deluje za vse vrednosti n, razen n = - 1 (ker ne moremo deliti z 0). Upoštevali smo najpreprostejši primer iskanja integrala. Na splošno reševanje integralov ni lahka naloga, izkušnje, ki so že bile pridobljene iz matematike, pa so v njej dobra pomoč. V zgornjem delu smo videli, da iz vsake formule diferenciacije dobimo ustrezno integracijsko formulo. Zato so vse možne možnosti že dolgo pridobljene in povzete v ustreznih tabelah. Naslednja tabela integralov vsebuje formule za integracijo osnovnih algebrskih funkcij. Te formule je treba zapomniti, jih zapomniti postopoma, saj so fiksne vaje. Druga tabela integralov vsebuje glavne trigonometrične funkcije: Izkazalo se je, da je za to zmožnost integracije, to je, da najdemo nedoločene integrale, zelo preprosta. V tem pomaga formula ustanoviteljev integro-diferencialnega računa Newton-Leibniz. V skladu s tem je v prvi fazi izračun želenega integrala sestavljen iz iskanja nedoločenega, nato izračuna vrednosti najdenega primitivnega F (x) z zamenjavo x, ki je enaka najprej zgornji meji, nato pa k nižji in končno določitvi razlike teh vrednosti. V tem primeru konstanta C ni mogoče zapisati. ker izgine pri odštevanju. Nekatere integrale obravnavamo s podrobno rešitvijo. Poiščite območje mesta pod enim valom sinusnega vala. Sedaj obravnavamo integrale s podrobno rešitvijo, ki uporablja lastnost aditivnosti v prvem primeru, in zamenjavo vmesne integracijske spremenljivke v drugem primeru. Izračunamo določen integral delno racionalne funkcije: y = (1 + t) / t 3 od t = 1 do t = 2. Sedaj bomo pokazali, kako poenostaviti jemanje integralov z uvedbo vmesne spremenljivke. Recimo, da morate izračunati integral iz (x + 1) 2 . Govorili smo o določenem integralu za končni interval [a, b] funkcije f (x), ki je nenehno na njem. Toda številni specifični problemi vodijo v potrebo po razširitvi koncepta integralov na primer, ko so meje (ena ali obe) enake neskončnosti ali ko je prekinjena funkcija. Na primer, pri izračunu površin pod krivuljami se asimptotično približujejo osi koordinat. Za razširitev koncepta integralov na ta primer se poleg prehoda na mejo pri izračunu Riemannove vsote približnih pravokotnikov izvede še ena. S takšnim dvojnim prehodom do meje dobimo neustrezen integral. Nasprotno pa se vsi zgoraj navedeni integrali imenujejo pravilni. 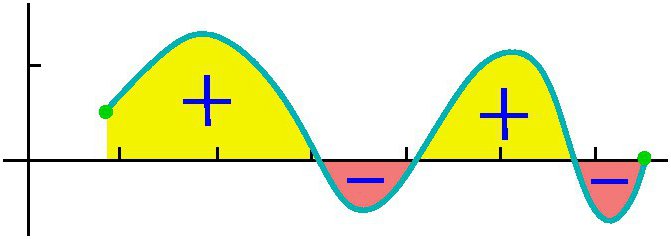 Tako bo za funkcijo, prikazano na zgornji sliki, določen integral od a do b (S1 + S3) - (S2 + S4).
Tako bo za funkcijo, prikazano na zgornji sliki, določen integral od a do b (S1 + S3) - (S2 + S4). Diferencial določenega integrala
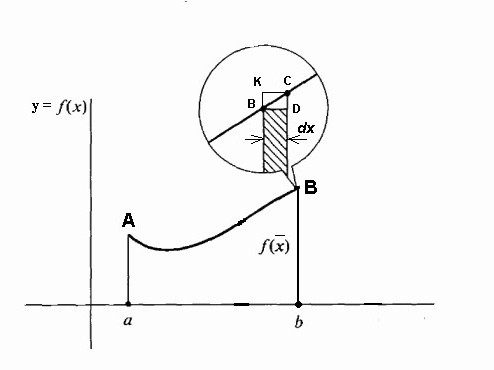 Pri fiksni liniji aA in premičnem Bb to območje postane funkcija f (x̃), pri čemer so inkrementi Δx along še vedno odloženi vzdolž osi x, in prirastki funkcije f (x̃) so inkrementi površine pod krivuljo.
Pri fiksni liniji aA in premičnem Bb to območje postane funkcija f (x̃), pri čemer so inkrementi Δx along še vedno odloženi vzdolž osi x, in prirastki funkcije f (x̃) so inkrementi površine pod krivuljo. 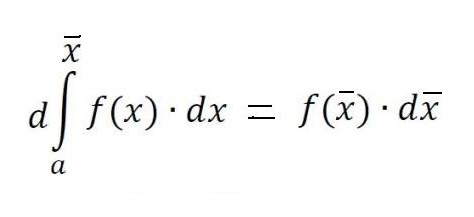
Temeljno razmerje integralnega računa
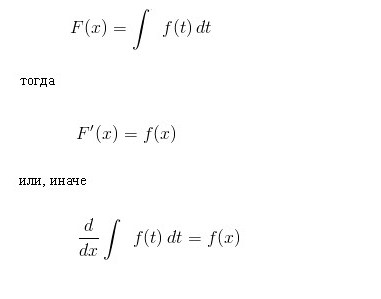
Osnovno pravilo integracije

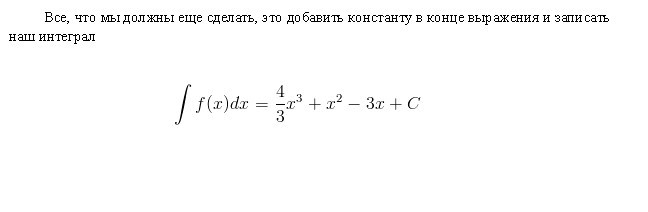

Integralne tabele
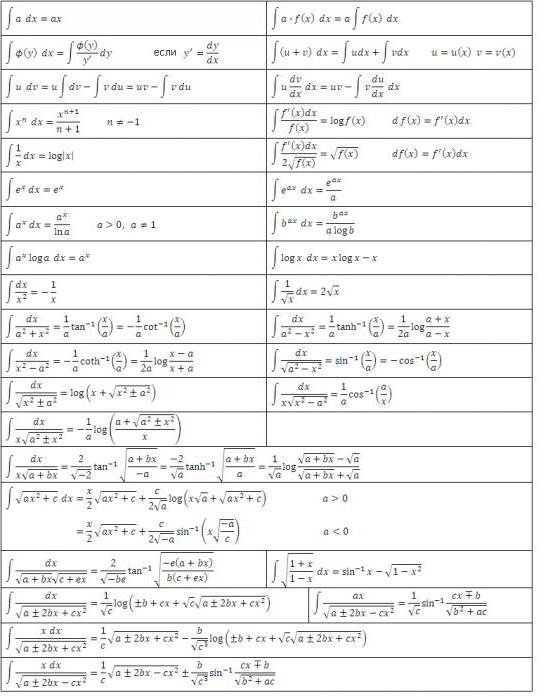

Kako izračunati določen integral
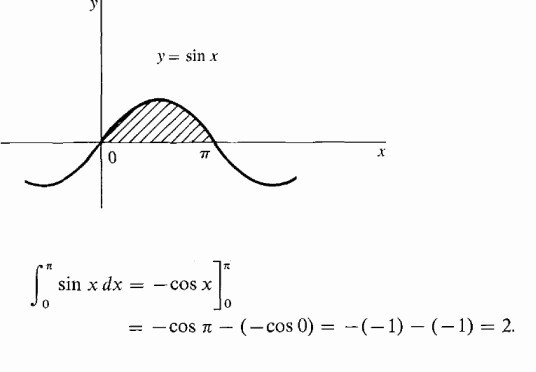 Izračunajte osenčeno območje pod hiperbolo.
Izračunajte osenčeno območje pod hiperbolo. 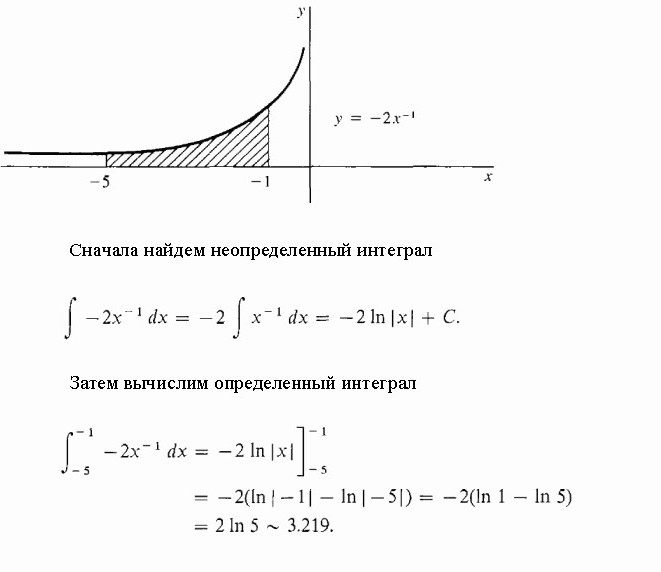
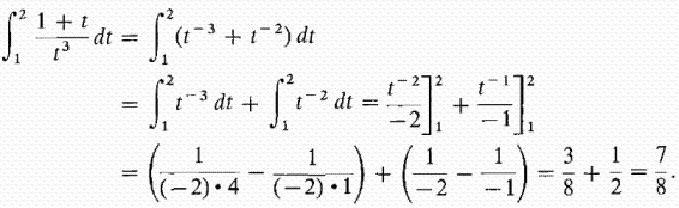
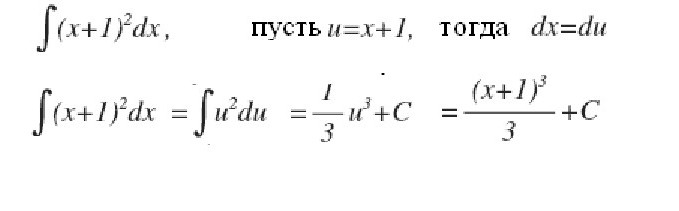
O nepravilnih integralih