Kaj je stožec? Koncept in fotografija

Stereometrija je pomemben del geometrije, katere predmet proučevanja so lastnosti in značilnosti številk v tridimenzionalnem prostoru. V tem članku bomo obravnavali eno od takšnih volumetričnih številk. Spoznajmo vprašanje, kaj je stožec.

Konična številka

Dajemo najbolj splošno definicijo stožca. Pod to sliko razumemo površino, ki nastane kot posledica povezovanja ravnih segmentov neke točke v prostoru z vsemi točkami dane krivulje. V tem primeru določena točka v prostoru ne sme biti v ravnini krivulje. Na primer, če ima krivulja obliko parabole, se bo številka, dobljena z opisano metodo, imenovala parabolični stožec, če je krivulja elipsa, bo stožec eliptična in tako naprej.

Po geometrični definiciji, kaj je stožec, predstavimo fotografijo, ki prikazuje vizualno možne oblike te številke.

Če pogledamo to fotografijo, so mnogi videli v njej otroški klobuk, ki ga je nosil Buratino, vafeljsko skodelico iz sladoleda v obliki roga ali opozorilni oranžni in črni črtasti cestni stožec.

Stožec geometrijskih elementov

Da bi bolje razumeli vprašanje, kaj je stožec, moramo navesti geometrijska imena elementov te prostorske figure.

Stožec je omejen z dvema površinama. Prvi se imenuje baza. To je ravnina, ki jo omejuje zgornja krivulja. Lahko je na primer krog ali elipsa. Druga površina je stran za obliko in se imenuje stožčasta. Ne leži v isti ravnini, ampak se lahko spremeni v ravno sliko, kot bo obravnavano spodaj.

Eden od pomembnih elementov stožca je njegov vrh. Ta točka omejuje konično površino. Vse točke osnovne krivulje so povezane z njo.

Segment, ki povezuje vrh osnove, imenuje se generica ali tvori stožec. Po drugi strani se je krivulja, ki meji na bazo, imenovala direktna ali vodilna figura.

Območja konične površine in podlage segajo do skupne površine stožca. Prostor, ki ga ti dve površini omejujeta, je prostornina stožca.

Okrogel ravni konus in njegove linearne značilnosti

Zgoraj je bila dana splošna opredelitev, kaj je stožec. Kljub temu pa pogosto v praksi in pri geometrijskih problemih obstaja specifična oblika te številke - ravna krožna stožca. To je prikazano spodaj.

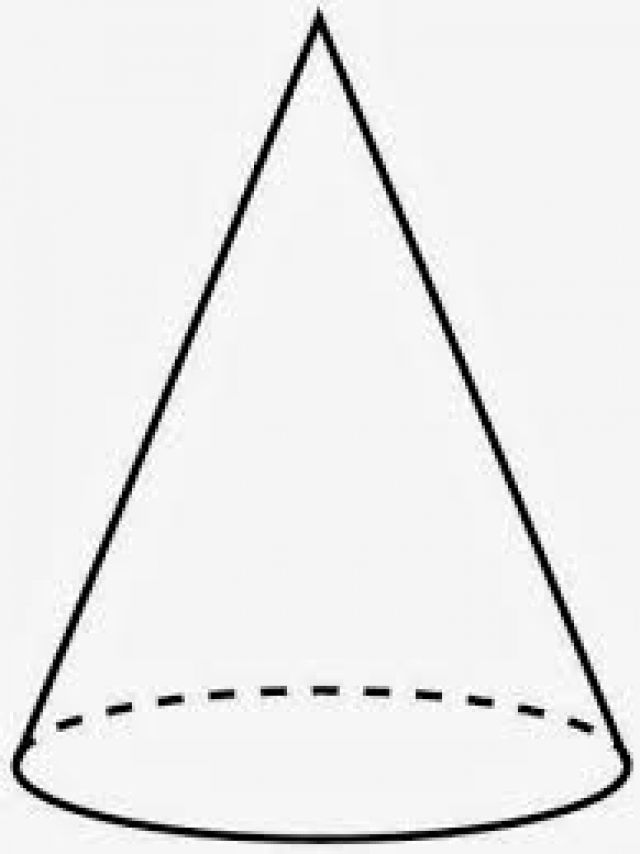
Osnova te številke je krog. Imenuje se naravnost, ker pravokotnica, ki je padla na svojo bazo z višine, preseže krog v njegovem natančnem središču. Če ta pogoj ni bil izpolnjen, lahko govorimo o nagnjenem stožcu.

Linija, ki povezuje vrh s središčem kroga, se imenuje os slike. To je tudi os vrtenja stožca. Dejansko, če vzamete pravokoten trikotnik in ga začnete vrteti okrog ene od nog, bo nastala slika ravno konus z okroglo osnovo. Ta metoda pridobivanja stožca je shematsko prikazana spodaj.

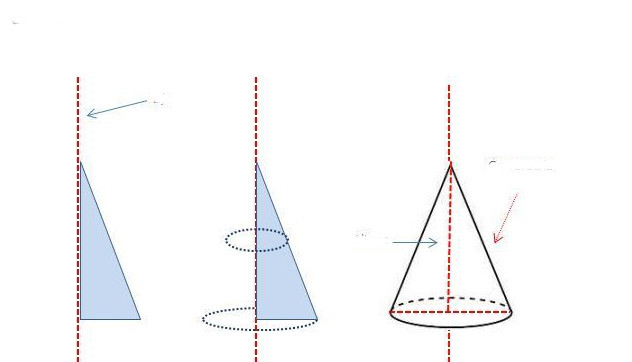
Vidimo lahko, da bo generator enak dolžini hipotenuze trikotnika. Noga, okoli katere je bila izvedena rotacija, bo postala višina za tridimenzionalno sliko, drugi pa bo enak polmeru stožca (polmer krožne osnove).

Ena od pomembnih značilnosti zadevne številke je, da so dolžine vseh generatorjev za to enake. To nam omogoča, da s pomočjo Pitagorejevega izreka napišemo matematično povezavo med tremi glavnimi linearnimi parametri oblike:

g ² = r ² + h ²

Kvadrat generatorja ravnega krožnega stožca g je enak vsoti kvadratov njegovega polmera r in višine h.

Po pregledu vprašanja, kaj je stožec ravna črta s krožnim dnom, pokažimo, kako je možna njegova površina in prostornina.

Določanje površine

Kot smo že omenili, je površina figure oblikovana s stožčasto površino in ravno podlago. Kakšno je njihovo območje? Z zaupanjem lahko odgovorite na to vprašanje, če pogledate ravno skeniranje krožnega stožca. Rezanje podlage s stranske ploskve in rezanje slednje vzdolž tvorbe, dobimo naslednji rezultat.

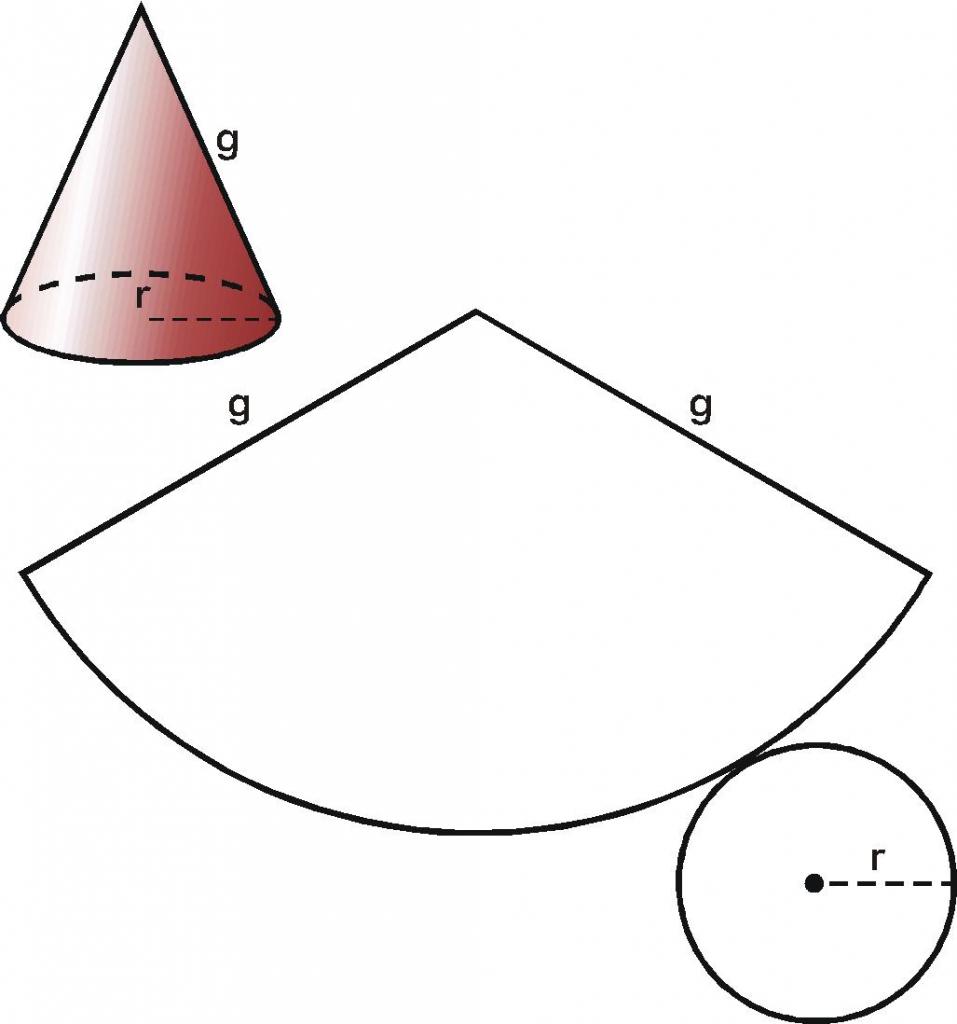
Pri določanju območja kroga ni težav. Formula za njeno področje je znana vsakemu študentu. Zapišite ga:

S _o = pi * r ²

Simbol S _o je območje podnožja slike.

Bočna površina stožca na ploskem skeniranju je predstavljena s krožnim sektorjem, katerega polmer je enak dolžini generatorja, dolžina loka, na katerem počiva sektor, pa je enaka dolžini oboda baze. Ti podatki nam omogočajo enkratno določitev področja sektorja. Ne bomo dali vmesnih izračunov za pridobitev formule za kvadrat S _b stranske površine stožca. Pišemo končni rezultat:

S _b = pi * g * r

Ker je generica g vedno večja od polmera r, bo površina stranske površine slike za vse parametre višja od površine podlage.

Formula za skupno površino ima obliko:

S = S _o + S _b = pi * r * (r + g)

Določanje obsega slike

Bralci so morda opazili, da oblika stožca spominja na nekaj piramide, le njena stranska površina je gladka in ne rebrasta, kot piramida. Ta analogija ima geometrijsko utemeljitev, saj se povečanje števila stranskih ploskev piramide v neskončnost prevede v stožec. To dejstvo omogoča, da za volumen stožca zapišemo točno enako formulo kot za volumen piramide. Imamo:

V = 1/3 * h * S _o

Upoštevajte, da ni pomembno, katera zaprta krivulja tvori osnovo stožca, prav tako ni pomembno, ali je številka ravna ali poševna, formula bo veljavna v vseh teh primerih.

Za stožec kroga, izraz za V ima določeno obliko:

V = 1/3 * pi * r ^{2 *} h

Naloga določanja območja stožca skozi njegov volumen

Pokažemo, kako uporabljati pisne formule.

Predpostavimo, da je volumen okroglega konusa 50 cm ³ . Njegovo površino je treba izračunati, če je polmer r trikrat manjši od višine h.

Zapišemo formulo za volumen in razmerje višine h s polmerom r v skladu s pogojem problema:

V = 1/3 * pi * r ^{2 *} h;

h = 3 * r.

Iz teh enačb dobimo:

V = 1/3 * pi * r ² * 3 * r =>

r = (V / pi) ≈ 2.516 cm;

h = 3 * ∛ (V / pi) ≈ 7.547 cm.

Dobljene vrednosti nam omogočajo izračun dolžine splošnega generatorja stožca:

g = √ (h ² + r ² ) = 7,955 cm.

Formula za površino številke je:

S = pi * r * (r + g)

Določili smo vse potrebne količine (r in g). Če nadomesti svoje numerične vrednosti v enakost, dobimo odgovor: S = 82,72 cm2.