Translacijsko gibanje: definicija, formule, izrek

Mehanika upošteva vse možne premike materialne točke in trdnega telesa. Vse so opisane v več poglavjih. Na primer, vprašanje, kako se premikajo, bo v pristojnosti kinematike. Podrobno opisuje translacijsko gibanje in bolj zapleteno rotacijsko gibanje. Prvič, to je lažje. Ker je brez tega težko preiti na naslednje teme.

Katere predpostavke dovoljuje mehanik?

V številnih problemih je dovoljeno uvesti približevanje. To je posledica dejstva, da to ne bo vplivalo na rezultat, vendar bo poenostavilo razmišljanje.

Prvi približek je povezan z velikostjo telesa. Če je obravnavano telo bistveno manjše od drugih v istem referenčnem okviru, potem so njegove dimenzije zanemarjene. In telo se spremeni v materialno točko.

Drugi je posledica odsotnosti deformacij v telesu med njegovim gibanjem. Ali celo tako nepomembna njena velikost, ki jo je mogoče popolnoma zanemariti.

Kaj je translacijsko gibanje telesa?

Za pojasnilo boste morali razmisliti o dveh točkah znotraj trdne snovi. Povezati morajo segment. Če ta segment med gibanjem ostane vzporeden z začetnim položajem, potem je rečeno, da gre za premik naprej.

Če je zanemarjena velikost telesa in se upošteva materialne točke Ta segment je odsoten in se premika vzdolž same črte.

Živahni primeri takšnega gibanja

Prva stvar, ki si jo morate zapomniti, je avto dvigala. Popolnoma ponazarja gibanje telesa naprej. Dvigalo se vedno premika povsem navzgor ali navzdol brez kakršnega koli rotiranja.

Naslednji primer, ki ponazarja translacijsko gibanje, je gibanje kabine Ferrisovega kolesa. Vendar je to resnično le v primeru, ko se rahlega nagiba kabine na začetku vsakega premika ne upošteva.

Tretja situacija, ko je mogoče govoriti o gibanju naprej, je povezana z gibanjem pedal za kolesa. Njihovo gibanje se smatra glede na okvir. Tudi tu se predpostavlja, da se stopala človeka med vožnjo ne nihajo.

Seznam se lahko dopolni s premikanjem batov, ki nihajo znotraj valjev motorja z notranjim zgorevanjem.

Glavni koncepti

Kinematika translacijskega gibanja je, da preučuje in opisuje gibanje trdnih in materialnih točk. Vendar pa ne upošteva razlogov, ki bi prisilili telo k temu. Za opis gibanja so potrebne koordinate, ki označujejo njen položaj v prostoru. Poleg tega je potrebno poznavanje hitrosti in v vsakem trenutku.

Najprej je treba spomniti na pot. To je črta, po kateri se je telo premaknilo.

Prvi je vstop v pot. Je vektor, ki je označen z latinično črko r. Lahko poveže izvor s položajem materialne točke. V drugih primerih je ta vektor narisan od začetne do končne točke poti. Enote premika so metri.

Druga vrednota, ki zasluži pozornost, je pot. Je enaka dolžini trajektorije, po kateri se telo premika. Pot je označena s črko latinico S, ki se meri tudi v metrih.

Osnovne formule

Zdaj je čas za hitrost. Je tudi vektor. Poleg tega označuje ne le smer gibanja telesa, temveč tudi hitrost njegovega gibanja. Vektor hitrosti je vedno usmerjen vzdolž tangentne črte, ki jo lahko narišemo na katerokoli točko poti. Označena je s črko V. Enote njene meritve so m / s.
Hitrost v vsakem trenutku gibanja lahko definiramo kot izpeljanko gibanja skozi čas. Če gre za težavo enotno gibanje, potem je veljavna naslednja formula:

• V = S: t, kjer je t čas gibanja.

V primeru spremembe smeri gibanja morate uporabiti vsoto vseh gibov.

Naslednja vrednost je pospešek. Še enkrat, vektorska količina, ki je usmerjena proti hitrosti z veliko vrednostjo. Opredeljen je kot prvi derivat hitrosti skozi čas. Sprejeta oznaka - črka "a". Dimenzija je navedena vm / s2.

Formule za vsako komponento pospeška, usmerjene vzdolž osi, izračunamo kot razmerje med spremembo hitrosti vzdolž te osi in časovnim intervalom. Če ustvarite matematični zapis, dobite naslednje:

• in _x = _{xV x} : .t.

Za projekcije pospeševanja na druge osi so formule podobne.
Poleg tega je pri premikanju vzdolž trajektorije z ovinkom možno vektor pospeška razgraditi v dva izraza:

• a = a _t + a _n , kjer je _t tangencialni pospešek, usmerjen vzdolž upogibnega tangenta, in _n je normalno, kar kaže na središče ukrivljenosti.

Translacijsko gibanje katerega koli trdnega telesa se zmanjša na opis gibanja le ene njegove točke. Uporabljajo se naslednje formule: t

• S = S ₀ + V ₀ t + (pri ² ): 2.
• V = V ₀ + pri.

V tej formuli indeksi "nič" označujejo začetne vrednosti količin.

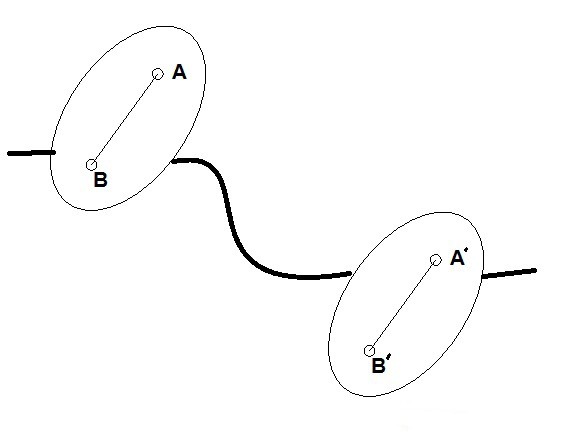
Teorem o prevodni magnitude

Njegova formulacija je naslednja: trajektorija, hitrost in pospešek vseh točk telesa so med gibanjem naprej enaki.

Da bi to dokazali, morate napisati formulo vektorski dodatki premik in vektor, ki povezujeta dve poljubni točki. Trajektorije vseh točk dobimo zaradi njihovega prenosa vzdolž drugega vektorja. Sčasoma pa ne spremeni svoje smeri in velikosti. Zato je mogoče trditi, da se vse točke telesa premikajo vzdolž enakih poti.

Če vzamemo časovni derivat, dobimo vrednost hitrosti. Poleg tega je izraz poenostavljen do te mere, da sta hitrosti obeh točk enaki.
Polje drugega časovnega derivata je rezultat enakega pospeška obeh točk.