Obod kvadrata in pravokotnika. Metode določanja in primeri rešitev.

Pogosto lahko na internetu najdete posmeh glede tega, kako znanje matematike - integrali, diferenciali, trigonometrične funkcije in drugi deli teme - ne pomagajo olajšati življenja posameznika. Takšne šale so zaman, saj pomaga pri pravilnem izračunu obsega kvadrata, pravokotnika in drugih geometrijskih oblik v gradbenih delih. Poraba materiala: ploščice, tapete, talne obloge - ni mogoče določiti brez razumevanja osnovnih matematičnih formul in geometrijskih oblik.

Kvadratne lastnosti

Vsi izračuni v matematiki temeljijo na lastnostih objekta. Da bi odgovorili na vprašanje: »Kaj je obod kvadrata?« - priporočamo, da se spomnimo posebnih značilnosti te številke.

1. Enakost vseh strank.
2. Prisotnost štirih kotov 90 stopinj.
3. Paralelnost strank.
4. Vrtljiva simetrija. Ko se slika vrti, njen videz ostane nespremenjen.
5. Sposobnost opisovanja in vstopa v krog.
6. Diagonale na presečišču se delijo na pol.
7. Območje slike označuje prostor, ki je zapolnjen s kvadratom v dvodimenzionalnem prostoru.
8. Obod številke ni nič drugega kot vsota dolžin njegovih strani.
9. Iz prejšnjega premoženja sledi, da bodo merilne enote perimetra enote dolžine: m, cm, dm in druge.

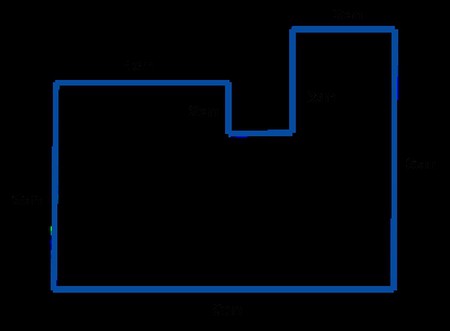
Če želite šteti podstavke za dokončanje popravil v kvadratni sobi, morate vedeti dolžino sobe. To naredite tako, da izračunate obseg.

Območje

Prevedeno iz grške besede pomeni "ukrep okoli". Izraz velja za vse zaprte oblike: kvadrat, krog, pravokotnik, trikotnik, trapez in druge. Poznavanje definicije perimetra osnovnih elementov je potrebno za reševanje kompleksnih geometrijskih problemov s predmeti nepravilne oblike. Če želite na primer izračunati podnožje v prostoru s postavitvijo tipa „G“ ali pa ga imenujemo tudi »zagon«, boste morali določiti obseg kvadrata in pravokotnika. Navsezadnje je oblika prostora sestavljena iz teh osnovnih elementov.

Standardna oznaka takšne velikosti je črka R. Vsaka slika ima ob upoštevanju svojih lastnosti svojo formulo za določanje obsega.

Lastnosti pravokotnika

1. Enakost nasprotnih strani.
2. Enakost diagonal.
3. Sposobnost opisovanja kroga.
4. Višine pravokotnika so enake njegovim stranicam.
5. Vsota kotov je 360 ​​stopinj in vsi koti so pravilni.
6. Paralelnost nasprotnih strani.
7. Pravokotnost sosednjih strani.
8. Vsota kvadratov diagonal pravokotnika je enaka vsoti kvadratov njegovih strani.
9. Sekajoči diagonali se delita na polovico.
10. Nezmožnost kroga v obliki.

Kvadrat površine

Glede na ugotovljene (znane) parametre kvadrata obstajajo različne formule za določanje njegovega oboda. Preprosta naloga je izračunati obseg ob določeni dolžini njegove strani. V tem primeru je R = с + с + с + с ali 4 * s. Na primer, dolžina strani kvadrata je 7 cm, potem je obod številke 28 cm (4 * 7).

V prvem primeru je vse jasno, vendar kako najti obod kvadrat, vedoč njegovo območje? In tukaj je vse zelo jasno. Ker je površina slike določena z množenjem ene strani z drugo, in vse strani so enake na kvadratu, je potrebno izvleči koren iz znane vrednosti. Primer: obstaja kvadrat s površino 25 dm ² . Koren 25 je 5 - ta vrednost označuje dolžino stranice kvadrata. Zdaj, ko nadomestimo najdeno vrednost - 5 dm ² - v izvirno perimetrsko formulo, lahko rešimo problem. Odgovor bo 20 dm. To je 4, pomnoženo s 5, prejel želeno vrednost.

Kvadrat in krog

Iz lastnosti obravnavane podobe se zdi, da je krog lahko vpisan v kvadrat in ga tudi opisati okoli slike.

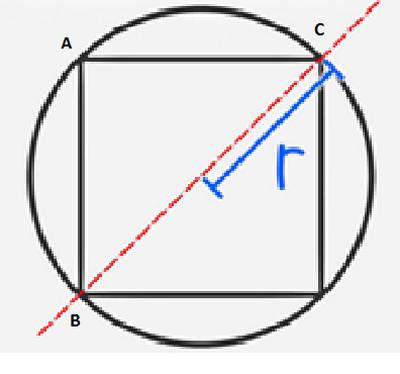
Prva možnost je najti obod ob obodu obkroža. Vpisan je kvadrat, katerega tocke so na krogu. Polmer kroga je 1/2 diagonalne dolžine. Izkazalo se je, da je premer enak diagonali. Zdaj morate razmisliti pravokotni trikotnik ki je bila posledica delitve diagonale kvadrata. Rešitev problema se zmanjša na iskanje strani tega trikotnika. BC je znana vrednost, premer krožnice. Recimo, da je enak 3 cm, Pitagorjev izrek v primeru enakih strani trikotnika bo izgledal takole: 2c ² = 3 ² . V formuli je simbol s dolžina strani trikotnika in kvadrata; 3 - znana vrednost hipotenuze. Zato je c = /9 / 2. Če poznamo stran kvadrata, ni mogoče izračunati njegovega oboda.

Značilnost vpisanega kroga je delitev strani kvadrata na pol. Zato je polmer enak polovici dolžine stranice kvadrata. Nato stran c = 2 * polmer. Območje kvadrata je v tem primeru 4 * 2 * polmer ali 8 polmerov kroga.

Obodni pravokotnik

Najosnovnejša formula za določanje obodnega pravokotnika preko znanih vrednosti njegovih strani je: P = 2 (a + b), pri čemer sta a in b dolžine strani slike.

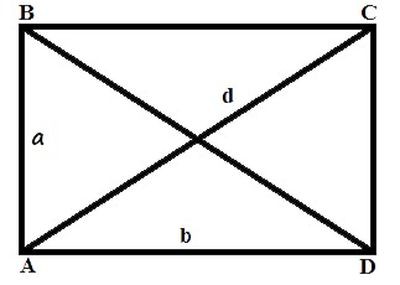
Diagonala pravokotnika, podobna kvadratu, deli sliko na polovico in tvori pravi trikotnik. Vendar je naloga zapletena zaradi dejstva, da so stranice tega trikotnika neenake. V primeru znane vrednosti ene od strani in diagonale lahko drugo najdemo tako, da sledimo Pitagorovu izreku: d ² = a ² + v ² , kjer sta a in v stran figure, d pa diagonal.

Če nobena od strank ni znana, potem pride v poštev poznavanje trigonometrije: sines, kosinus in druge funkcije.

Iskanje oboda vzdolž omejene kroge in znanega premera se zmanjša na dejstvo, da je premer enak dolžini diagonale slike. Nadalje je rešitev problema določena s prisotnostjo znanih količin. Če so podani koti, potem skozi trigonometrične funkcije. Če je stran dana, bo odgovor našel skozi Pitagorejski izrek.

Pravokotnik in trigonometrične funkcije

Za jasnost je primer reševanja problema. Glede na: pravokotnik AVSD; dolžina diagonale ( d ) 20 cm; kot f - 30 °. Poiščite obod slike.

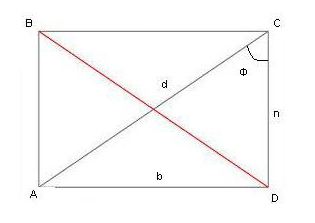
Iz trigonometrije je treba spomniti na naslednje: sinus kota v pravokotnem trikotniku je enak razmerju nasprotne noge do hipotenuze. Sinus 30 ° (obstajajo tabele, s katerimi lahko določimo vrednosti trigonometričnih funkcij za pravilne kote) je 1/2. Izkazalo se je 1/2 = razmerje v d . Neznana vrednost v bo enaka d / 2 = 20/2 = 10 cm.

Če želite izračunati obseg, morate najti drugo stran slike. To je mogoče preko Pitagorovega izreka, saj sta dolžini hipotenuze in eni od nog znani, ali spet skozi razmerje med kosinusom kota.

Kosinus kota as je izražen kot razmerje med sosednjim krakom in hipotenuzo in je enako /3 / 2.

/3 / 2 = n / d , n = (d * )3) / 2 ali 10 * .3. Po izvlečenju korena iz 3 dobimo dolžino strani trikotnika: 10 * 1,73 = 17,3 cm.

Obod je 2 (17,3 + 10) = 2 * 27,3 = 54,6 cm.

Perimeter in Attitude

V šolskem programu se pojavljajo težave v geometriji, ko so dolžine strani pravokotnika izražene z njihovo medsebojno povezavo. Obravnava rešitve tega problema je predstavljena v nadaljevanju.

Znano je, da je vsota dolžin vseh strani pravokotnika, to je njenega oboda, 84 cm, razmerje med dolžino (d) in širino (w) pa je 3: 2. Poiščite strani slike.

Rešitev: naj bo dolžina 3x in širina 2x glede na razmerje iz stanja problema. Formula oboda pravokotnika s podatki o dolžinah stranic bo naslednja: 3x + 3x + 2x + 2x = 84. Nadalje, 10x = 84, x = 8,4 cm, z zamenjavo x v izraz dolžine in širine pravokotnika, lahko najdemo želene vrednosti. Dolžina: 3 * 8,4 = 25,2 cm; širina: 2 * 8,4 = 16,8 cm.

Članek je namenjen reševanju najpogostejših nalog v šolskem kurikulumu. In to niso vsi načini za iskanje obodnega kvadrata in pravokotnika.