Koncept pospeševanja. Gibanje s konstantnim pospeškom. Formule in primerne naloge

Kinematika je del mehanike gibanja v fiziki, ki obravnava proučevanje in opis gibanja teles. V članku so predstavljene osnovne vrednosti, ki opisujejo mehansko gibanje. Razmislite, kaj je pospeševanje in gibanje s stalnim pospeševanjem, predstavljamo ustrezne formule.

Tri kinematike

Te vrednosti so pot L, hitrost v in pospešek a¯. Prvi je skalar in se meri v metrih, drugi in tretji sta vektorski vrednosti, ki sta izraženi v metrih na sekundo in v metrih na kvadratni sekundi. Vse enote ustrezajo sistemu SI.

Glede na definicijo je hitrost hitrost gibanja telesa v prostoru, to je:

v¯ = dL / dt

Po drugi strani pa je pospešek hitrost spremembe hitrosti, ki se matematično zapiše kot:

a¯ = dv¯ / dt

Smiselno je upoštevati kinematične značilnosti glede na določeno pot gibanja. Slednji so lahko pravokotni ali ukrivljeni. Smer polnega pospeška je odvisna od vrste poti. Hitrost je usmerjena proti poti, ki je vedno tangencialna.

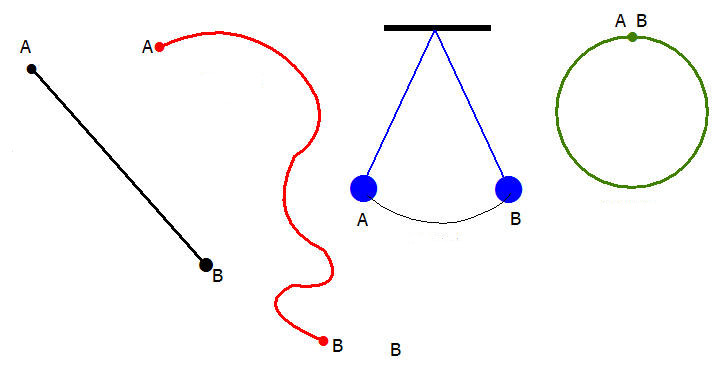
Značilnosti pospeševanja med vožnjo po krivulji

Ker je pospešek numerična značilnost spremembe hitrosti, edinstveno opisuje vse vidike te spremembe. Govorimo ne le o absolutni vrednosti, ampak tudi o vektorju smeri v¯. Sprememba velikosti hitrosti opisuje tangencialni ali tangencialni pospešek. Usmerjena je bodisi proti vektorju hitrosti ali proti njej. Formula za izračun je:

a _t = dv / dt

Ko se telo giblje v krivulji, na primer v krogu, vrednost vp nenehno spreminja svojo smer. Kaj je razlog za to spremembo? Vsebuje delovanje na telo normalnega ali centripetalnega pospeška. Ta vrednost je usmerjena pravokotno na linijo trajektorije in se izračuna po formuli:

a _n = v2 / r

Kjer je v absolutna vrednost hitrosti, je r ukrivljenost krivulje (polmer kroga).

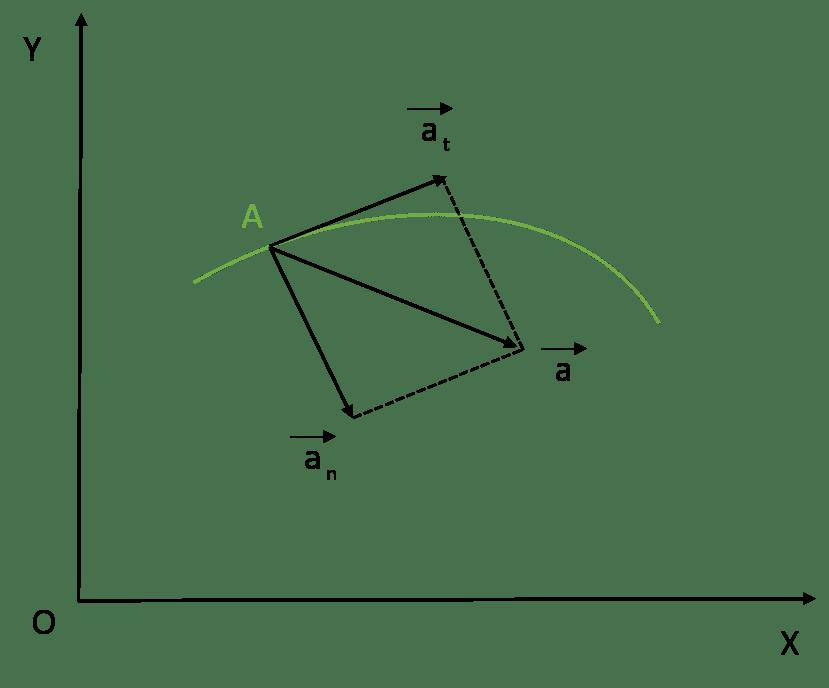
Obe komponenti polnega pospeška nam omogočata, da jo določimo z uporabo te enakosti:

a = √ (a _t ² + a _n ² )

Upoštevajte, da gibanje po ukrivljeni poti vedno pomeni, da ima telo dve komponenti pospeševanja.

Gibanje s konstantnim pospeškom v ravni črti

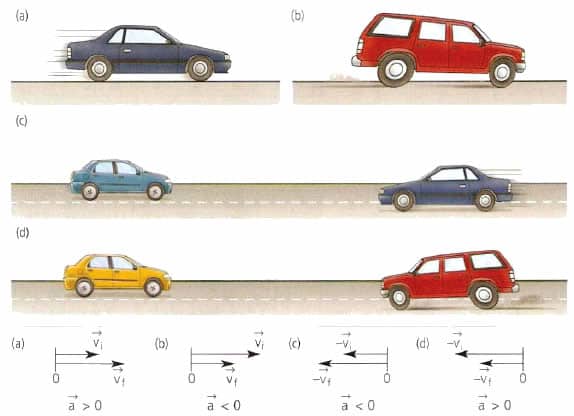
Če je trajektorija ravna, je proučevanje procesa gibanja zelo olajšano. Dejstvo je, da je s takim gibanjem hitrost vedno usmerjena v eno smer, kar pomeni, da normalna komponenta pospeška ni prisotna. Polni pospešek s pravokotnim gibanjem je edinstveno določen s tangencialno komponento. Nadalje bomo v članku obravnavali samo gibanje vzdolž premice, zato se bo količina a imenovala preprosto pospeševanje.

Posebno pozornost je treba posvetiti procesu premikanja telesa v ravni liniji, ki se izvaja s stalnim pospeševanjem. Za tako premik preprosto napišite matematične enačbe gibanja. O njih bomo razpravljali spodaj.

Primeri gibanja teles s konstantnim pospeševanjem so pospešek avtomobila od začetka, prosti padec teles v enotnem gravitacijskem polju in zaviranje vozil.

Formule za hitrost

Glede na pospešek in gibanje s stalnim pospeševanjem v 10. razredu srednjih šol se učenci naučijo formul za določanje hitrosti in prevožene razdalje. Začnimo s formulami za hitrost.

Recimo, da je bilo telo v mirovanju, potem se je začelo gibati s stalnim pospeševanjem. Kako se bo spreminjala hitrost? Odgovor na to vprašanje vsebuje naslednjo enakost:

v = a * t

To pomeni, da se bo hitrost linearno povečevala. Koeficient sorazmernosti med vrednostmi v in t je pospešek a.

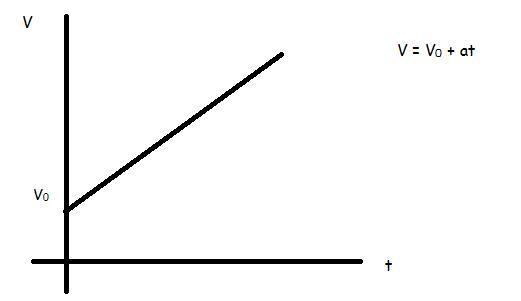
Zdaj si predstavljajte situacijo, da se je telo gibalo s konstantno hitrostjo v ₀ , nato pa se je začelo pospeševati. Kako se bo spremenila prejšnja formula za hitrost? Izgledala bo:

v = v ₀ + a * t.

Upoštevajte, da se odštevanje časa v tej formuli začne od trenutka, ko se v telesu pojavi pospešek.

Predpostavimo zdaj tretjo možnost: namesto pospeševanja gibanja v prejšnjem primeru se je telo začelo upočasniti. V tem primeru uporabite izraz:

v = v ₀ - a * t.

V vseh treh primerih so grafi hitrosti proti času ravne črte.

Formule za pot

Glede na temo pospeševanja in gibanja s konstantnim pospeškom premice je treba predstaviti tudi formule za pot, ki jo prevaža telo. Konec koncev je v praksi smiselna ta kinematična količina.

Ustrezne formule za L lahko dobimo, če za zgornje izraze za hitrosti vzamemo integral skozi čas. Spodaj so zapisane tri formule:

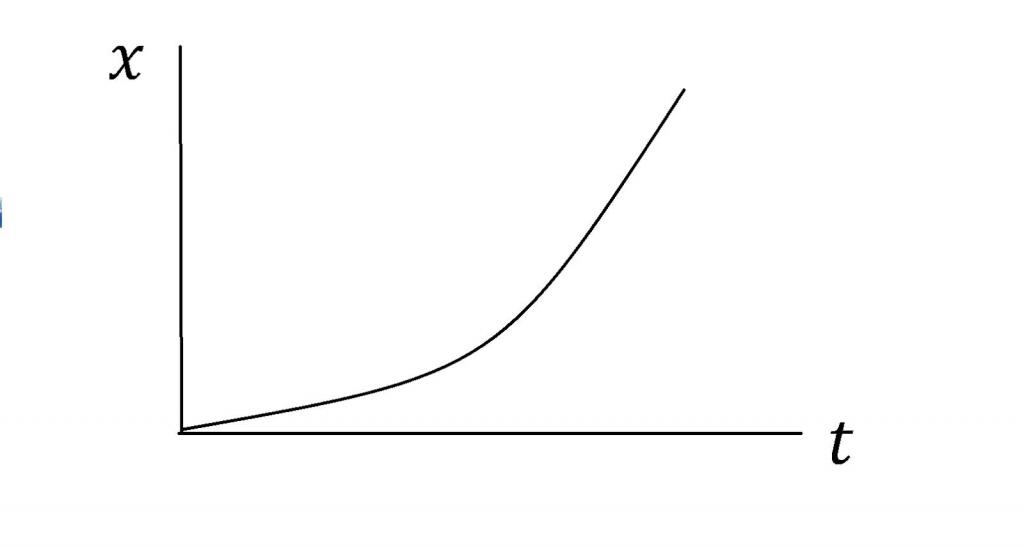
L = a * t 2/2;

L = v ₀ * t + a * t 2/2;

L = v ₀ * t - a * t 2/2

Prvi izraz definira pot za čisto gibanje s konstantnim pospeševanjem, druga enačba opisuje pospešeno gibanje z nično začetno hitrostjo, tretja formula pa se uporablja za izračun zaviralne poti z enako počasnim gibanjem.

Naloga dvigovanja telesa v gravitacijsko polje

Kot je navedeno zgoraj, pride do prostega padca s stalnim pospeševanjem. Za gibanje s pospeškom je značilna konstanta g, ki je blizu površine našega planeta enaka 9,81 m / s2.

Znano je, da je bilo telo vrženo navpično. Začetna hitrost je 30 m / s. Potrebno je izračunati višino, na katero se telo dvigne.

Ta naloga je tipičen problem za enako premikanje v ravni črti. Označimo višino vzpona s črko h. To bo enako poti, po kateri bo telo letelo, dokler se ne bo ustavil v višini. Ta višina je enaka:

h = v ₀ * t - g * t 2/2

Čas letenja se lahko določi iz pogoja enakosti vrednosti v proti ničli na točki največje višine, to je:

v = v ₀ - g * t = 0 =>

t = v ₀ / g

Če nadomestimo enakost za t v formulo za h, dobimo:

h = v ₀ ² / g - g * (v ₀ / g) 2/2 = v ₀ ² / (2 * g)

Če nadomestimo vrednost začetne hitrosti, pridemo do odgovora: h = 45,9 metrov.