Znaki podobnosti trikotnikov in njihova praktična uporaba za reševanje problemov

Pojem podobnosti poljuben geometrijske oblike v bistvu je zelo enostavno razložiti in še manj dokazati. Tako, na primer, gledamo predmet skozi povečevalno steklo in vidimo podobo tega predmeta, ki se je večkrat povečal, pri čemer so ohranili deleže vseh njegovih dimenzij. Z drugimi besedami, slika objekta je podobna izvirnemu predmetu pred povečavo. V večini problemov geometrije, da dokaže sorazmernost strani in področja trikotnika uporabite glavne 3 znake. Da bi upoštevali obstoječe znake podobnosti trikotnikov, je treba na začetku opredeliti ključni koncept, ki bo v prihodnosti uporabljen v besedilu.

Torej so trikotniki podobni, če so njihove podobno nameščene strani sorazmerne, in ustrezno razporejeni koti so enaki (je treba spomniti, da se strani imenujejo podobne ali ustrezne, če so nameščene nasproti enakim kotom). Upoštevajte podobne trikotnike CABC in 1A ₁ B ₁ C ₁ . V skladu z zgornjim konceptom so upoštevne stranke: AB in A ₁ B ₁ , pa tudi pari strani BC in B ₁ C ₁ , AC in A ₁ C ₁ . Upoštevajte, da so stranice vsakega od teh treh parov nasprotnih kotov iste velikosti.

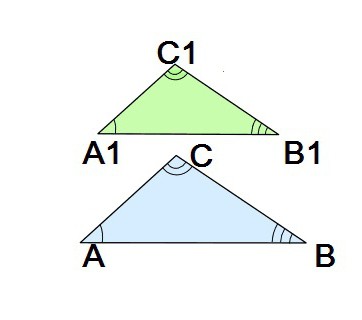Podobnost je označena z posebnega znaka med oznakami zadevnih številk: CABC ₁ ∆ A ₁ B ₁ C ₁ .

Razmerje med zadevnimi strankami in prisotnostjo te funkcije je parameter, imenovan koeficient podobnosti k. Če je k = 2, lahko rečemo, da je ena od dveh upoštevanih geometričnih številk povečana dvojna kopija druge. Jasno je, da če so k = 1, so trikotniki enaki. Tako se lahko ta enakost obravnava kot poseben primer njihove podobnosti.

Znaki podobnosti trikotnikov

Izkazalo se je, da za ugotovitev prisotnosti obravnavane značilnosti ni treba preverjati vseh zahtev, navedenih v besedilu zgoraj navedene opredelitve podobnosti. Dovolj je, da izpolnimo minimalni sklop pogojev in to bomo zdaj potrdili v praksi.

Prvi znak

Pri reševanju problemov se prvi znak podobnosti trikotnikov pojavlja v dokazih veliko pogosteje kot drugi. Upoštevajte, da deluje le z dvema elementoma geometrijske figure: dvema kotoma. Preostali znaki podobnosti trikotnikov zahtevajo sodelovanje treh elementov. Torej sta za dva poljubna podobna trikotnika dva kota ene izmed njih enaka istim 2 kotom drugega.

Dokaz

Glede na osnovne lastnosti, ki veljajo za poljuben trikotnik, lahko za .C zapišemo naslednji izraz. Njegova vrednost bo enaka (180 ° - (+А + ∠V)), za drugo theS _{1 pa bo} vrednost izračunana po istem principu. Z osnovnimi transformacijami izrazov dobimo, da je ∠C = C ₁ . Tako so vsi koti, ki so prisotni v ВАВС, enaki vsem analognim kotom, ki se nahajajo v 1А ₁ В ₁ С ₁ . S podobnim algoritmom so dokazani preostali znaki podobnosti trikotnikov.

Drugi znak

Ta pristop k dokazovanju se pogosto uporablja, če so znani koti obravnavanih geometričnih številk.

Za dva podobna trikotnika je res, da sta obe strani vsake od njiju sorazmerni z dvema podobnima stranema drugega, koti med temi pari strani pa so enaki.

Dokaz

Za dokazovanje te funkcije se morate sklicevati na prejšnje izračune. Na podlagi zgornjih rezultatov je dovolj dokazati, da je =В = V ₁ . Razmislite o CABC ₂ , za katero so v skladu s prvim znakom izpolnjene naslednje trditve: = ₁ = ∠A ₁ , =2 = V ₁ . CABC ₂ ~ 1A ₁ В ₁ С ₁ . To pomeni AB / A ₁ B ₁ = AC ₂ / A ₁ C. Po drugi strani je znano iz pogoja, da velja naslednje razmerje: AC / A ₁ C _{1 =} AB / A ₁ B ₁ . Posledično dobimo enakost strani AC = AC ₂ , kot tudi trditev, da je CABC ~ accordingABC ₂ po drugem znaku (AC = AC ₂ in =A = ∠1, ker je bilo zaradi upoštevanja začetnih podatkov ugotovljeno, da je A = 1A ₁ in = ₁ = 1A ₁ , AB- je skupna stran za ta dva trikotnika). Iz dokaza sledi, da ∠B = ∠2, in ker =2 = 1V ₁ , dobimo V = V ₁ . Iz tega sledi, da je dokazan še en znak.

Tretji znak

Ta lastnost velja za najbolj očitno pri dokazovanju podobnosti, saj se upoštevajo vse strani teh trikotnikov z znanimi parametri.

Torej, za dva trikotnika, ki sta si podobna, obstaja trditev, da so 3 strani ene izmed njih sorazmerne s tremi ustreznimi stranmi drugega.

Dokaz

Glede na prejšnjo značilnost podobnosti, zdaj za konstruiranje dokaza zadostuje ugotoviti le, da obstaja enakost oblike: =A = 1A ₁ . V ta namen upoštevajte poljubno CABC ₂ , za katero ∠1 = 1A ₁ , 2 = V ₁ . Glede na 1. atribut ∆ABC _{2 2} ∆A ₁ B ₁ C ₁ , lahko za ta dva trikotnika zapišemo razmerje tipa AB / A ₁ B ₁ = BC ₂ / B ₁ C ₁ = C ₂ A / C ₁ A _1, iz katerega lahko zapišemo enakost oblike: B ₁ C ₁ = BC ₂ , A ₁ C ₁ = AC ₂ . Iz tega je logično sklepati, da CABC ∆ ABC _2, in kot zaključek, AndA in 1A ₁ sta enaka. Iz tega sledi, da je dokazana tudi obravnavana značilnost.

Lastnosti

1. Za dva trikotnika, ki sta si podobna, je razmerje med vrednostmi njihovih območij neposredno sorazmerno s kvadratom koeficienta. Dokaz. Razmislite o dveh poljubnih številkah s tremi stranicami in tremi koti, ki sta si podobni. Naj bodo A in A ₁ ustrezne strani teh številk, h in h ₁ pa pripadajoče višine. Naj bo k koeficient podobnosti za obravnavane trikotnike, zato lahko iz razmerja napisa napišemo enačbo oblike: A ₁ = k * A. Vidimo lahko, da lahko za razmerje višin zapišemo enačbo oblike: h ₁ = k * h. Za razmerje površin obravnavanih geometričnih številk dobimo: S ₁ / S = (1 / 2a ₁ h ₁ ) / (1 / 2ah) = (a ₁ / a) * (h ₁ / h) = k * k = k ² . Torej, ko je trikotnik »raztegnjen« za 2-krat, se njegova površina poveča za 2 ² = 4-krat. Druga lastnina izhaja iz prejšnjega dokaza in je z njo neposredno povezana.
2. Vse ustrezne črte, narisane v takšnih trikotnikih, so prav tako sorazmerne in enake vrednosti zgoraj prikazanega koeficienta. To pomeni, da je po navedenem premoženju mogoče trditi, da bodo vse notranje dodatne konstrukcije tudi sorazmerne.

Dodatek k glavnemu seznamu znakov

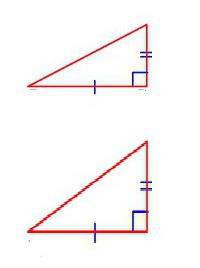
Vredno je razmisliti o številnih posameznih značilnostih, ki veljajo za geometrijske oblike določenega tipa. Pravi trikotniki so podobni, če:

• njihova hipotenuza in katerikoli od obeh nog sta proporcionalni;
• če so njihovi ustrezni ostri koti enaki;
• če so vse noge obravnavanih trikotnikov po paru sorazmerne.

Zaključek

Tako smo združili vse možne znake, s katerimi lahko nekako dokažemo podobnost dveh ali več figur s tremi vogali in stranicami, ne glede na njihovo vrsto in lastnosti. Pri večini problemov v geometriji se za dokazovanje sorazmernosti strani in območij uporabljajo glavni trije znaki, vendar nismo prezrli številnih znakov podobnosti, ki se lahko uporabijo le, če je potrebno dokazati, da so zadevne geometrijske figure pod pravim kotom. Ti znaki podobnosti desni trikotniki bistveno poenostavi postopek reševanja različnih vrst nalog in za njih potrebuje najmanj podatkov.