Kvadratne enačbe. Reševanje kvadratnih enačb
Sprva se zdi, da je ta tema zapletena zaradi mnogih, ki niso zelo preproste formule. Ne samo, da imajo kvadratne enačbe dolge vnose, temveč tudi korenine najdemo skozi diskriminantno. Obstaja skupno tri nove formule. Ne zlahka se spomnite. To je možno šele po pogosti rešitvi takšnih enačb. Potem se bodo vse formule spominjale same.

Splošni pogled kvadratne enačbe
Tu se ponudi eksplicitni zapis, ko se najprej zabeleži največja stopnja, nato pa - v padajočem vrstnem redu. Pogosto obstajajo situacije, ko so komponente v nasprotju. Potem je bolje, da enačbo prepišemo v padajočem vrstnem redu stopnje spremenljivke.
Predstavimo zapis. Predstavljeni so v spodnji tabeli.
| Oznaka velikosti | Njeno ime |
| a, b, c | koeficienti, ki so poljubne številke |
| x | spremenljivko |
| D | diskriminantno |
| x 1 x 2 | korenine enačbe |
Če sprejmemo te oznake, se vse kvadratne enačbe zmanjšajo na naslednji vnos.
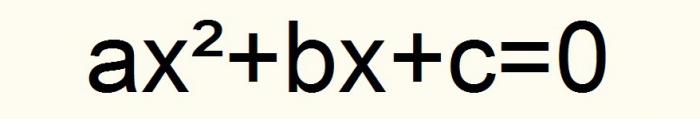
Poleg tega je koeficient a Let 0. Naj bo ta formula označena s številko ena.
Ko je enačba podana, ni jasno, koliko korenin bo v odgovoru. Ker je ena od treh možnosti vedno mogoča:
- rešitev bo imela dve koreni;
- odgovor je ena številka;
- korenine enačbe sploh ne bodo.
In čeprav odločitev ni zaključena, je težko razumeti, katera od možnosti bo padla v določenem primeru.
Vrste zapisov kvadratnih enačb
V nalogah so lahko različni vnosi. Ne bodo vedno izgledale kot splošna formula za kvadratno enačbo. Včasih bo zamudil nekaj predmetov. Kar je bilo napisano zgoraj, je popolna enačba. Če v njem odstranite drugi ali tretji izraz, dobite nekaj drugega. Te zapise imenujemo tudi kvadratne enačbe, le nepopolne.
Poleg tega lahko izginejo samo izrazi, katerih koeficienti so »v« in »c«. Število "a" v nobenem primeru ne more biti nič. Ker se v tem primeru formula spremeni v linearno enačbo. Formule za nepopolno obliko enačb so naslednje:
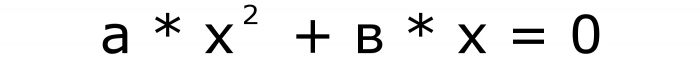
in
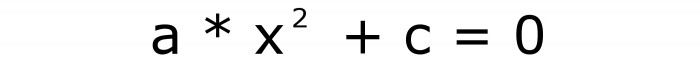
Torej, obstajata samo dve vrsti, poleg polnih, obstajajo tudi nepopolne kvadratne enačbe. Naj bo prva formula številka dve, druga tri.
Diskriminantna in odvisnost števila korenin od njegove vrednosti
Če želite izračunati, morate to številko poznati korenine enačbe. Vedno se lahko izračuna, ne glede na formulo kvadratne enačbe. Da bi izračunali diskriminantno, morate uporabiti spodnjo enačbo, ki bo imela številko štiri.

Po zamenjavi vrednosti koeficientov v tej formuli lahko dobite številke z različnimi znaki. Če je odgovor pritrdilen, potem je odgovor na enačbo dva različna korena. Pri negativnem številu bodo korenine kvadratne enačbe odsotne. V primeru njegove enakosti na nič bo odgovor en.
Kako je rešena kvadratna enačba popolne oblike?
Dejansko se je to vprašanje že začelo obravnavati. Ker morate najprej najti diskriminanta. Ko je jasno, da obstajajo korenine kvadratne enačbe in je njihovo število znano, je treba uporabiti formule za spremenljivke. Če obstajata dve koreni, potem morate uporabiti to formulo.
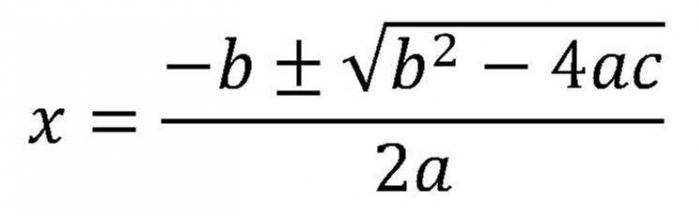
Ker je v njem znak ±, bosta dve vrednosti. Izraz kvadratnega korena je diskriminanten. Zato lahko formulo prepišemo drugače.
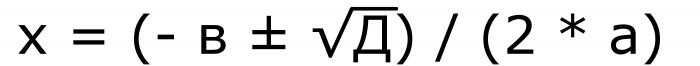
Formula 5. Iz istega zapisa je jasno, da če je diskriminant nič, potem bosta oba korena vzela iste vrednosti.
Če rešitev kvadratnih enačb še ni bila rešena, je bolje, da vrednosti vseh koeficientov zapišemo pred uporabo diskriminantnih in spremenljivih formul. Kasneje ta trenutek ne bo povzročil težav. Toda na samem začetku je zmeda.
Kako je rešena kvadratna nepopolna enačba?
Vse je veliko preprostejše. Tudi ni potrebe po dodatnih formulah. In ne potrebujejo tistih, ki so že zabeleženi za diskriminantno in neznano.
Najprej upoštevamo nepopolno enačbo številka dve. Pri tej enakosti se predpostavlja, da se neznana vrednost umakne iz oklepaja in reši linearno enačbo, ki bo ostala v oklepajih. Odgovor bo dva korena. Prvi je nujno enak nič, ker obstaja faktor, ki je sestavljen iz same spremenljivke. Druga odločitev bo izšla linearna enačba.
Nepopolna enačba številka tri je rešena s prenosom števila z leve strani enakosti na desno. Potem morate deliti s koeficientom, ki je obrnjen proti neznanemu. Ostaja le izvleček kvadratni koren in zapomnite si, da jo dvakrat zapišete z nasprotnimi znaki.

Koristni nasveti
Nato zapišemo nekaj dejanj, ki nam pomagajo pri učenju, kako rešiti vse vrste enakosti, ki se spremenijo v kvadratne enačbe. Študentom bodo pomagali, da se izognejo nepazljivim napakam. Te pomanjkljivosti so vzrok za slabe ocene pri preučevanju obsežne teme "Kvadratne enačbe (razred 8)". Posledično teh ukrepov ne bo treba stalno izvajati. Ker bo obstajala stalna spretnost.
- Najprej morate napisati enačbo v standardni obliki. To pomeni, najprej izraz z največjo stopnjo spremenljivke, nato pa - brez stopnje in zadnje - samo številko.
- Če se pred koeficientom „a“ pojavi minus, potem lahko delo za začetnika zaplete pri študiju kvadratnih enačb. Bolje je, da se ga znebite. V ta namen se mora vsa enakost pomnožiti z "-1". To pomeni, da bodo vsi izrazi spremenili znak v nasprotno.
- Na enak način se priporoča, da se znebite frakcij. Enostavno enačbo preprosto pomnožimo z ustreznim množiteljem, da zmanjšamo imenovalce.

Primeri
Potrebne so naslednje kvadratne enačbe:
x2 - 7x = 0;
5x2 - 30 = 0;
15 - 2x - x 2 = 0;
x 2 + 8 + 3x = 0;
12x + x2 + 36 = 0;
(x + 1) 2 + x + 1 = (x + 1) (x + 2).
Prva enačba: x 2 - 7x = 0. Je nepopolna, zato je rešena, kot je opisano za formulo 2.
Po vstavitvi oklepajev x (x - 7) = 0.
Prvi koren prevzame vrednost: x 1 = 0. Drugi se najde iz linearne enačbe: x - 7 = 0. Ni težko opaziti, da je x 2 = 7.
Druga enačba: 5x 2 + 30 = 0. Ponovno nepopolna. Rešeno je le, kot je opisano za tretjo formulo.
Po prenosu 30 na desno stran enačbe: 5x 2 = 30. Sedaj morate deliti s 5. Izkazalo se je: x 2 = 6. Odgovori bodo številke: x 1 = ,6, x 2 = - √6.
Tretja enačba: 15 - 2x - x 2 = 0. V nadaljevanju bo rešitev kvadratnih enačb začela s ponovnim zapisovanjem v standardno obliko: - x 2 - 2x + 15 = 0. Zdaj je čas, da uporabimo drugi koristni nasvet in pomnožimo vse z minus eno. . Izkazalo se je, da je x 2 + 2x - 15 = 0. Po četrti formuli je treba izračunati diskriminantno: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. To je pozitivno število. Iz zgoraj povedanega izhaja, da ima enačba dva korena. Izračunati jih je treba s peto formulo. To pomeni, da je x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Potem x 1 = 3, x 2 = - 5.
Četrta enačba x 2 + 8 + 3x = 0 se pretvori v to: x 2 + 3x + 8 = 0. Njena diskriminantna je enaka tej vrednosti: -23. Ker je ta številka negativna, bo odgovor na to nalogo naslednji: "Ni korenin."
Peto enačbo 12x + x 2 + 36 = 0 je treba ponovno napisati na naslednji način: x 2 + 12x + 36 = 0. Po uporabi formule za diskriminantno dobimo številko nič. To pomeni, da bo imel en koren, in sicer: x = -12 / (2 * 1) = -6.
Šesta enačba (x + 1) 2 + x + 1 = (x + 1) (x + 2) zahteva transformacije, ki se nanašajo na to, da se taki izrazi uvedejo pred odpiranjem oklepajev. Na mestu prvega bo naslednji izraz: x 2 + 2x + 1. Po enakosti se bo pojavil ta zapis: x 2 + 3x + 2. Po tem, ko bodo taki izrazi prešteti, bo enačba izgledala takole: x 2 - x = 0. spremenila se je v nepopoln . Podobno mu je bilo že malo več. Korenine tega bodo številke 0 in 1.