Poincarejeva domneva: zgodovina problema, dokaz, pomen

V šoli so vsi seznanjeni s koncepti izreka in hipoteze. Praviloma so v življenju prizadeti najpreprostejši in najbolj primitivni zakoni, matematiki pa zelo zapletene predpostavke in predstavljajo zanimive probleme. Ne vedno, sami uspejo najti rešitve in dokaze, v nekaterih primerih pa se njihovi privrženci in samo kolegi borijo že vrsto let.

Inštitut Clay je leta 2000 sestavil seznam 7 tako imenovanih izzivov tisočletja po analogiji s seznamom hipotez, ki so bili sestavljeni leta 1900. Skoraj vse te naloge so bile zdaj rešene, le ena od njih se je preselila v posodobljeno različico. Sedaj je seznam težav naslednji:

• Hodgeova domneva;
• enakost razredov P in NP;
• Poincarejeva domneva;
• Yang-Millsova teorija;
• Riemannova hipoteza;
• obstoj in gladkost reševanja Navier-Stokesovih enačb;
• Birch-Swinnerton-Dyerove domneve.

Vse matematike pripadajo različnim disciplinam in so pomembne. Na primer, Navier-Stokesove enačbe se nanašajo na hidrodinamiko, vendar lahko v praksi opišejo obnašanje snovi v zemeljski magmi ali so koristne pri napovedovanju vremena. Toda vsi ti problemi še vedno iščejo svoj dokaz ali zanikanje. Razen enega.

Poincarev izrek

Precej težko je s preprostimi besedami razložiti, v čem je težava, vendar lahko poskusite. Predstavljajte si kroglo, na primer mehurček. Vse točke njegove površine so enako oddaljene od njegovega središča, ki mu ne pripada. Toda to je dvodimenzionalno telo in hipoteza govori o tridimenzionalnosti. To je že nemogoče zamisliti, vendar imamo teoretično matematiko. V tem primeru se bodo vse točke tega telesa prav tako odstranile iz centra.

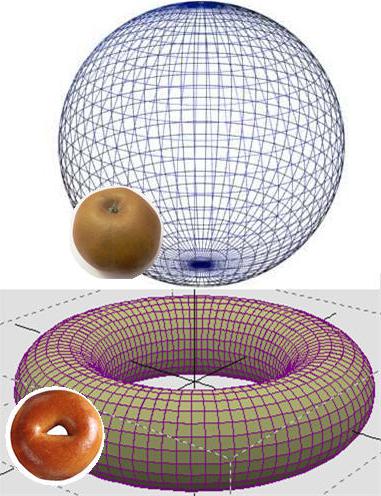
Ta problem se nanaša na topologijo - znanost o lastnostih geometrijskih oblik. Eden od temeljnih pojmov v njem je homeomorfizem, to je visoka stopnja podobnosti. Za primer si lahko predstavljate žogo in torus. Ene številke ne moremo dobiti iz druge, izogibajoč se razpokam, toda stožec, kocka ali valj iz prvega lahko dobimo zelo enostavno. Tu je Poincarejeva hipoteza, ki je namenjena tem metamorfozam z eno samo razliko - govorimo o večdimenzionalnem prostoru in telesih.

Zgodovina

Francoski matematik Henri Poincare študiral različna področja znanosti. O njegovih dosežkih lahko rečemo, na primer, da je popolnoma neodvisno od Alberta Einsteina predstavil glavne določbe posebna teorija relativnosti. Leta 1904 je izpostavil problem dokazovanja, da je vsako tridimenzionalno telo, ki ima določene lastnosti krogle, ravno do deformacije. Kasneje so ga razširili in posplošili ter postali poseben primer Thurstonove hipoteze, oblikovane leta 1982.

Besedilo

Poincaré je na začetku zapustil takšno izjavo: vsak preprosto povezan kompaktni tridimenzionalni kolektor brez meje je homeomorfen tridimenzionalni krogli. Kasneje so ga razširili in posplošili. In še dolgo je bila prvotna naloga, ki je povzročila največ težav, in je bila rešena le 100 let po njeni pojavnosti.

Razlaga in pomen

To je homeomorfizem, o katerem smo že razpravljali. Zdaj je vredno govoriti o kompaktnosti in singularnosti. Prvo pomeni le, da ima sorta omejene velikosti, ne more biti neprekinjeno in neskončno raztegnjena.

Kar se tiče edinstvenosti, lahko poskusite dati preprost primer. Dvodimenzionalna sfera - jabolko - ima eno zanimivo lastnost. Če vzamete običajno zaprto gumo in jo pritrdite na površino, lahko gladko deformacijo zmanjšate na eno točko. To je lastnost edinstvenosti, vendar jo predstavimo v odnosu do tridimenzionalni prostor precej težko.

Preprosto rečeno, problematično je bilo dokazati, da je singularnost edinstvena lastnost za kroglo. Če pa se, sorazmerno gledano, izkušnje z gumijastim trakom končajo s takim rezultatom, potem mu je telo homeomorfno. Kar zadeva uporabo te teorije v življenju, je Poincare verjel, da je vesolje v nekem smislu tridimenzionalno kroglo.

Dokaz

Ne mislite, da je več deset matematikov, ki so delali po vsem svetu, nihče ni napredoval ene jote, reševanje tega problema. Nasprotno, prišlo je do napredka in na koncu je privedlo do rezultata. Poincaré sam ni imel časa, da bi dokončal delo, vendar so njegove raziskave resno napredovale celotno topologijo.

V tridesetih letih se je zanimanje za hipotezo vrnilo. Najprej je bilo besedilo razširjeno na "n-dimenzionalni prostor", nato pa je ameriški Whitehead poročal o uspešnih dokazih, ki so ga pozneje opustili. V 60-70-ih letih sta dva matematika naenkrat - Smale in Stallings - skoraj istočasno, vendar sta na različne načine razvila rešitev za vse n več kot 4.

Leta 1982 in za 4 so našli dokaze, preostali so le 3. V istem letu je Thurston oblikoval hipotezo o geometrizaciji in Poincaréjeva teorija je postala njen poseben primer.

Potem je bilo delo nekoliko zastalo - ameriški Richard Hamilton je predlagal uporabo Ricci toka v rešitvi, vendar je naletel na težave in ni končal raziskave.

20 let je bila hipoteza Poincaréja, kot bi bila pozabljena. Leta 2002 je ruski matematik Grigorij Perelman predstavil rešitev na splošno, šest mesecev pozneje pa je naredil nekaj dodatkov. Kasneje so te dokaze preizkusili ameriški in kitajski znanstveniki. In sam Perelman se je zdel izgubil vse zanimanje za problem, čeprav je rešil bolj splošen problem geometrizacije, za katerega je Poincaréjeva domneva le poseben primer.

Priznavanje in vrednotenje

Seveda je to takoj postalo občutek, ker rešitve ene od težav tisočletja preprosto ni bilo mogoče spregledati. Še bolj presenetljivo je bilo dejstvo, da je Gregory Perelman zavrnil vse nagrade in nagrade, saj je dejal, da je že imel čudovito življenje. V glavah navadnih ljudi je takoj postal primer tistega pol-norega genija, ki ga zanima le znanost.

Vse to je povzročilo veliko razprav v tisku in medijih, da je priljubljenost matematika postala njegova. Poleti leta 2014 je obstajala informacija, da je Perelman odšel na delo na Švedsko, vendar se je izkazalo, da je to le govorica, da še vedno skromno živi v Sankt Peterburgu in komaj komunicira z nikomer. Med nagradami, ki so mu bile podeljene, niso bile le nagrade Clay Institute, ampak tudi prestižna Fields medalja, vendar je vse zavrnil. Vendar pa tudi Hamilton, ki je po Perelmanovih ocenah prispeval k dokazovanju, ni bil pozabljen. Leta 2009 in 2011 je prejel tudi prestižne nagrade in priznanja.

Kulturna refleksija

Kljub dejstvu, da za navadne državljane tako izjavo kot rešitev te težave ni smiselno, so dokazi postali znani precej hitro. Leta 2008 je japonski režiser Masahito Kasuga ob tej priložnosti posnel dokumentarec "Dokumentarni film o očaranju Poincaréja", posvečen 100-letnim poskusom reševanja tega problema.

Mnogi matematiki, vključeni v ta problem, so sodelovali pri streljanju, a glavni lik, Grigorij Perelman, tega ni hotel storiti. V streljanje so bili vključeni tudi njegovi ali njegovi bližnji prijatelji. Dokumentarni film, ki se je pojavil na zaslonih ob javnem odmevu v zvezi z zavrnitvijo znanstvenika, da bi sprejel nagrado, je v nekaterih krogih dobil slavo in prejel tudi več nagrad. Kot za množična kultura, navadni ljudje se še vedno sprašujejo, kakšne argumente je vodil peterburški matematik, zavračal denar, ko bi ga lahko dal na primer v dobrodelne namene.