Ostrogradsky - Gaussov izrek in formula

Mv Ostrogradsky - ruski matematik in fizik od ruskega imperija, akademik. Veliko je prispeval k razvoju matematična analiza teorija verjetnosti, mehanika (oddelek fizike) teorija števil. Leta 1826 je izpeljal formulo, ki se zdaj imenuje Ostrogradsky-Gaussova formula.

Zgodovina odkrivanja

Ostrogradsko-Gaussovo formulo je Joseph Lagrange prvič omenil leta 1762.

Nadalje je glavni način zmanjševanja trojnega integrala na površino dokazal Karl Gauss, ki je kot podlago za dokaz uporabil reševanje problemov v elektrodinamiki. To se je zgodilo v prvi polovici XIX. Stoletja.

Poleg tega je formulo v splošni obliki predstavil Mihail Ostrogradski. S svojo pomočjo je bilo možno izraziti vrednost razlike v parametru iz N-kratnega integrala.

Pomen formule Ostrogradsky

Ostrogradsky-Gaussova formula povezuje trojni integral nad prostorskim volumnom z integralno površino na obrazu. Gre za analog Greenove formule, ki povezuje dvojni integral nad ravnino s krivočrtno vzdolž njenih meja.

Izpeljava formule

Ostrogradsky - Gaussova formula: zaključek. Predpostavimo, da je v domeni W definirana integrandska funkcija R (x, y, z), ki je dokončna in kontinuirana. Njegov derivat je podoben na celotnem področju W, vključno z njegovo mejo. V tej obliki je zdaj znan Ostrogradski - Gaussov izrek (formula je podana spodaj).

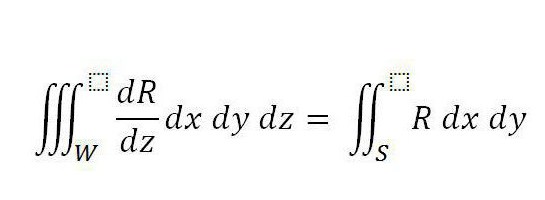
Še več, S je površina, ki povezuje telo, in integralni del na desni je razdeljen na njegovo zunanjo stran.

In popolnoma res

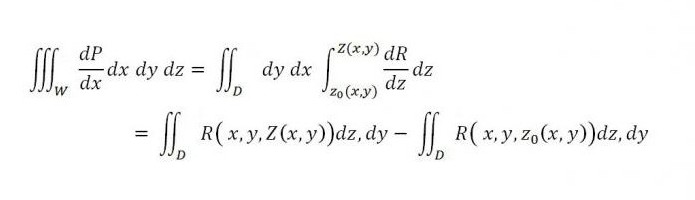
Če podobno upoštevamo integrale na površini, potem

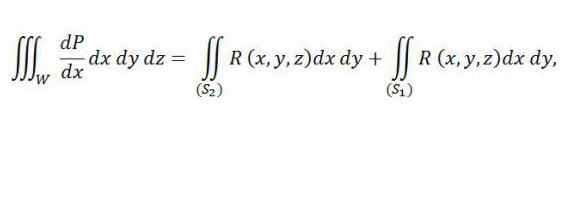
medtem ko je na desni vsota dveh integralov - prva je povezana z zgornjim delom površine (S ₂ ), drugi pa z nižjim delom površine (S ₁ ). Če k tej enakosti na desni dodamo spodaj navedeni integral, potem njegova veljavnost ne bo kršena:

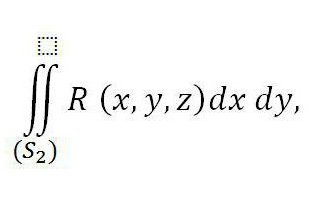
Ustreza zunanjemu delu površine S3 zaradi enakosti nič.

Če združimo vse tri zgoraj navedene integrale v eno, bomo dobili poseben primer Ostrogradske formule.

Enostavno se lahko zavedamo, da ta formula velja za širši razred teles in velja tudi za številke, omejene z absolutno nelinearnimi površinami.

Podobno veljajo naslednje formule:

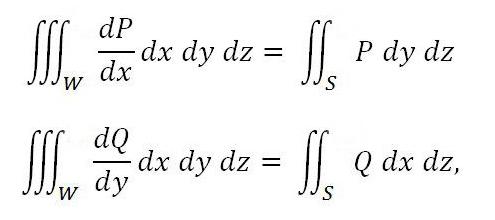
če so funkcije Q in P neprekinjene v domeni skupaj z njihovimi izvedenimi dP / dx in dQ / dy.

Če dodamo obe enakosti, dobimo izraz za formulo Ostrogradsky. Prikazuje integralno površino, povezano z zunanjim delom površine, skozi trojni integral, ki je prevzet nad samo telo, katerega meja je zgoraj omenjena površina.

Treba je razumeti, da formule Green, Stokes in Ostrogradsky izražajo integral, ki je povezan z določenim geometrijskim telesom, skozi integral, ki je vzet na njegovi meji. Greenova formula se uporablja samo v primeru dvodimenzionalnosti prostora, Stokesova formula se uporablja za ukrivljen dvodimenzionalni prostor.

Newton-Leibnizovo formulo lahko obravnavamo tudi kot nekakšen analog teh formul, ampak za enodimenzionalni prostor.

Uporaba te formule

Dovoljeno je neprekinjeno delovanje A, B in C v kateri koli nezaprti regiji prostora, pri čemer lahko za vsako zaprto površino, ki je v danem območju in omejuje določeno telo, upoštevamo naslednji integral po površini:

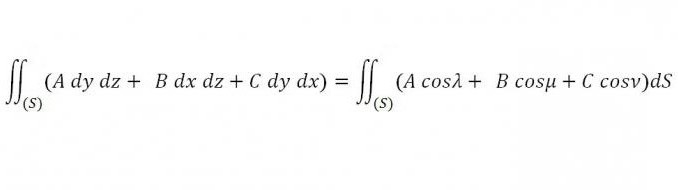
Treba je najti takšne vrednosti A, B in C, da je za vsak x, y in z ta integral enak nič.

Za to uporabite formulo Ostrogradsky-Gauss. Eden od implicitnih pogojev je gotovost in kontinuiteta funkcij A, B in C ter njihovih izvedenih finančnih instrumentov.

Prav tako je treba posebej uvesti najbolj dano omejitev za dani primer: tako telo in površina, ki ju omejujeta, morata biti hkrati v določenem in določenem območju, ki se imenuje preprosto povezana. Njegova glavna značilnost je odsotnost praznega prostora (vključno s točkovnim prostorom). Tako bo meja telesa ena in s tem ena sama površina.

Po uporabi formule je mogoče pridobiti naslednji pogoj, ki je zadosten:

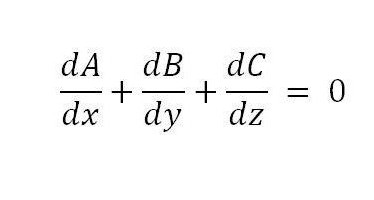
Da bi dokazali, da je pogoj tudi potreben, zadostuje uporaba diferenciacije trojnega integrala.

Za zaključek je treba povedati o področjih uporabe.

Kako se v praksi uporablja formula Ostrogradsky-Gauss? Primeri uporabe se nahajajo na različnih področjih: izpeljevanje nekaterih formul v fiziki (npr. Difuzijska enačba), pretvorba integralov, izračun Gaussovih integralov, dokazovanje nekaterih formul in še veliko več.