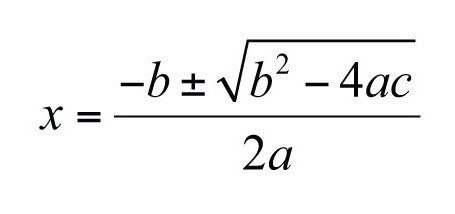Kako najti koren enačbe: linearno, kvadratno, kubično?

Enačbe v matematiki so enako pomembne kot glagoli v ruskem jeziku. Brez možnosti, da bi našli koren enačbe, je težko trditi, da je študent obvladal tečaj algebre. Poleg tega za vsako od njihovih vrst obstajajo posebne rešitve.

Kaj je to?

Enačba sta dva poljubna izraza, ki vsebujejo spremenljivke z enakovrednim znakom med njimi. Poleg tega je lahko število neznanih količin poljubno. Najmanjše število je eno.

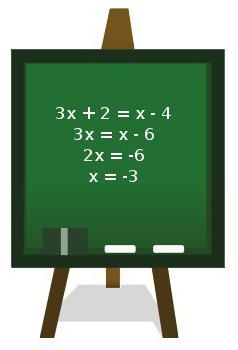
Rešitev je, da ugotovimo, ali obstaja koren enačbe. To je številka, ki jo spremeni v pravilno enakost. Če ne, potem je odgovor izjava, da "ni korenin". Lahko pa je nasprotno, če je odgovor množica številk.

Kakšne enačbe obstajajo?

Linearna. Vsebuje spremenljivko, katere stopnja je enaka eni.

• Trg. Spremenljivka ima moč 2 ali pa taka stopnja transformacije.
• Enačba najvišje stopnje.
• Frakcijsko racionalno. Ko je spremenljivka v imenovalcu frakcije.
• Z modulom.
• Iracionalno To je tisti, ki vsebuje algebrski koren.

Kako je rešena linearna enačba?

Je glavni. V ta namen si vsi drugi prizadevajo voditi. Ker je enostavno najti koren enačbe.

• Najprej morate izvesti možne transformacije, torej razširiti oklepaje in podati podobne izraze.
• Premakni vse monomiale s spremenljivko na levo stran enačbe, tako da prosti izrazi ostanejo na desni.
• V vsakem delu enačbe rešite podobne izraze.
• V enakopravnosti, ki izhaja iz leve polovice, bo rezultat koeficienta in spremenljivke, v desni polovici pa število.
• Še vedno je treba najti koren enačbe, ki deli število na desni, s koeficientom pred neznanim.

Kako najti korenine kvadratne enačbe?

Prvič, treba ga je skrčiti na standardni obrazec, to pomeni, da je treba odpreti vse oklepaje, vpisati je treba podobne izraze in vse monomiale premakniti na levo stran. Na desni strani enakosti mora ostati samo nič.

• Uporabite diskriminantno formulo. Kvadratiranje koeficienta pred neznanim s stopnjo "1". Pomnožite prost monomial in številko pred spremenljivko v kvadratu s številko 4. Izdelek odštejte od nastalega kvadrata.
• Ocenite vrednost diskriminanta. Negativno je - odločitev je končana, saj nima korenin. Enako nič - odgovor je ena številka. Pozitivna - dve vrednosti spremenljivke.

• 

  Poiščite dve koreni enačbe po formuli, v kateri kvadratni koren od diskriminantnega se odšteje ali doda negativnemu koeficientu spremenljivke v prvi stopnji. Nato z dvojnim koeficientom delimo kvadrat neznanega. (V primeru enakosti diskriminantne osebe je treba dodati ali odšteti ničlo, tako da bosta obe koreni sovpadali.)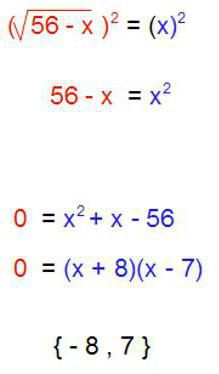

Kako rešiti kubično enačbo?

Najprej poiščite koren enačbe x. Določa se z metodo izbire iz številk, ki so delitelji prostega termina. Ta metoda je primerna za obravnavo posebnega primera. Naj bo enačba: x ³ - 3x ² - 4x + 12 = 0.

Njegov prosti izraz je 12. Potem bodo delitelji, ki jih je treba preveriti, pozitivni in negativni: 1, 2, 3, 4, 6 in 12. Iskanje se lahko zaključi na številki 2. Daje pravo enakost v enačbi. To pomeni, da se njegova leva stran izkaže za nič. Številka 2 je prva kubični koren enačbe.

Zdaj morate razdeliti prvotno enačbo z razliko med spremenljivko in prvim korenom. V posebnem primeru je to (x - 2). Preprosta transformacija vodi v takšno faktorizacijo števca: (x - 2) (x + 2) (x - 3). Isti faktorji števca in imenovalca se zmanjšajo, preostala dva oklepaja v razkritju pa navajata preprosto kvadratno enačbo: x ² - x - 6 = 0.

Tukaj najdemo dva korena enačbe po načelu, opisanem v prejšnjem oddelku. To so številke: 3 in -2.

Torej ima konkretna kubična enačba tri korenine: 2, -2 in 3.

Kako so rešeni sistemi linearne enačbe?

Tukaj je predlagana metoda za odpravo neznank. Sestoji iz izražanja enega neznanega skozi drugega v eni enačbi in zamenjavo tega izraza v drugo. Poleg tega je rešitev sistema dveh enačb z dvema neznankama vedno par spremenljivk.

Če so spremenljivke v njih označene s črkami x ₁ in x ₂ , potem lahko izpeljemo iz prve enačbe, na primer x ₂ . Nato se nadomesti v drugo. Izvedena je potrebna transformacija: razkritje oklepajev in prisila podobnih članov. Izkaže se preprosta linearna enačba, katere koren je enostavno izračunati.

Zdaj pa pojdite nazaj k prvi enačbi in poiščite koren enačbe x ₂ , pri čemer uporabite nastalo enačbo. Ti dve številki sta odgovor.

Preprost nasvet

Da bi bili prepričani o prejetem odgovoru, je priporočljivo, da vedno preverite. Ni potrebno pisati.

Če je ena enačba rešena, mora biti vsaka njena korenina zamenjana v prvotno enakost in dobiti enake številke v obeh delih. Vse se je združilo - prava odločitev.

Pri delu s sistemom je potrebno v vsaki rešitvi nadomestiti korenine in izvesti vsa možna dejanja. Izkazalo se je, da je prava enakost? Torej je odločitev pravilna.