Kako najti polmer kroga. Vpisana in omejena krog

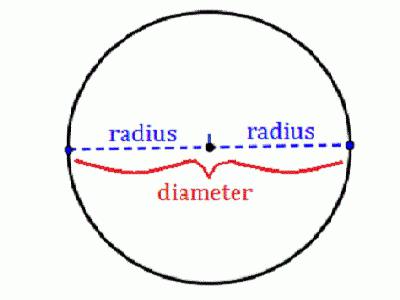
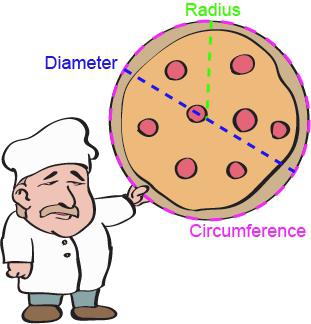
Polmer je segment, ki povezuje katerokoli točko kroga s središčem. To je ena od najpomembnejših značilnosti te številke, saj lahko na podlagi nje izračunate vse ostale parametre. Če veste, kako najti polmer kroga, lahko izračunate njegov premer, dolžino in območje. V primeru, da je ta številka napisana ali opisana okoli drugega, je mogoče rešiti več nalog. Danes bomo preučili osnovne formule in značilnosti njihove uporabe.

Znane vrednosti

Če veste, kako najti polmer kroga, ki je običajno označen s črko R, se lahko izračuna iz ene značilnosti. Te vrednosti vključujejo:

• obseg (C);
• premer (D) je segment (oziroma prej tetiva), ki poteka skozi osrednjo točko;
• območje (S) - prostor, ki je omejen na to številko.

Po obodu

Če je vrednost C znana v problemu, potem je R = C / (2 * P). Ta formula je izpeljana. Če vemo, kaj je to dolžina oboda potem ga ni treba zapomniti. Recimo, da je pri problemu C = 20 m. Kako najti polmer kroga v tem primeru? Znano vrednost preprosto nadomestite z zgornjo formulo. Upoštevajte, da se pri takih problemih vedno uporablja poznavanje števila P. Za udobje izračunov je njegova vrednost 3.14. Rešitev v tem primeru je naslednja: zapišite, katere vrednosti so podane, izpišite formulo in izvedite izračune. V odgovoru pišemo, da je polmer 20 / (2 * 3,14) = 3,19 m. Pomembno je, da ne pozabimo na tisto, kar smo mislili, in da omenimo ime merskih enot.

S premerom

Takoj poudarjamo, da je to najpreprostejša vrsta problema, ki se sprašuje, kako najti polmer kroga. Če dobite tak primer na nadzor, potem ste lahko mirni. Ne potrebuje niti kalkulatorja! Kot smo rekli, je premer segment ali, bolj pravilno, tetiva, ki prehaja skozi središče. Poleg tega so vse točke kroga enako oddaljene. Zato je ta tetiva sestavljena iz dveh polovic. Vsak od njih je radij, ki izhaja iz njegove definicije kot segmenta, ki povezuje točko na krogu in njegovo središče. Če je premer problema znan, potem, da bi našli radij, morate to vrednost razdeliti za dve. Formula je naslednja: R = D / 2. Če je premer v problemu 10 m, je polmer 5 metrov.

Po območju kroga

Ta vrsta naloge se običajno imenuje najtežja. To je predvsem posledica pomanjkanja poznavanja formule. Če veste, kako v tem primeru najti polmer kroga, je ostalo stvar tehnike. V kalkulatorju morate vnaprej najti samo ikono kvadratnega korena. Območje kroga je produkt števila P in polmer, pomnožen sam s seboj. Formula je naslednja: S = P * R ² . Če ločimo radij na eni strani enačbe, lahko zlahka rešite problem. Enako bo kvadratni koren iz kvocienta površine, deljene s številom P. Če je S = 10 m, potem je R = 1,78 metra. Kot pri prejšnjih nalogah je pomembno tudi, da ne pozabite na uporabljene enote.

Kako najti polmer obkroža

Recimo, da so a, b, c stranice trikotnika. Če poznate njihove vrednosti, lahko najdete polmer kroga, opisanega okoli njega. Če želite to narediti, morate najprej najti pol-perimeter trikotnika. Za lažje branje označimo z majhno črko str. Enaka polovici zneska strank. Njegova formula je: p = (a + b + c) / 2.

Izračunajte tudi produkt dolžine strani. Za priročnost jo označimo s črko S. Formula za polmer opisne kroge bo izgledala takole: R = S / (4 * √ (p * (p - a) * (p - b) * (p - c)).

Razmislite o primerni nalogi. Imamo krog, opisan okoli trikotnika. Dolžine njegovih stranic so 5, 6 in 7 cm, najprej izračunamo pol-perimeter. V našem problemu bo enaka 9 centimetrov. Zdaj izračunamo produkt dolžin strani - 210. Rezultate vmesnih izračunov nadomestimo s formulo in ugotovimo rezultat. Polmer omejene kroge je 3,57 cm. Odgovor zapišemo, ne da bi pozabili na merske enote.

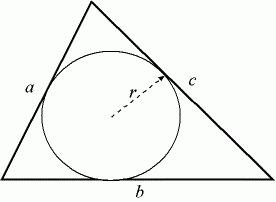
Kako najti polmer vpisanega kroga

Denimo, da so a, b, c dolžine strani trikotnika. Če poznate njihove vrednosti, lahko najdete polmer kroga, ki je vpisan. Najprej morate najti njegovo pol-perimeter. Za lažje razumevanje jo označujemo z majhno črko str. Formula za izračun je naslednja: p = (a + b + c) / 2. Ta vrsta naloge je nekoliko enostavnejša od prejšnje, zato vmesni izračuni niso več potrebni.

Polmer vpisanega kroga se izračuna po naslednji formuli: R = √ ((p - a) * (p - b) * (p - c) / p). Razmislite o tem s posebnim primerom. Predpostavimo, da problem opisuje trikotnik s stranicami 5, 7 in 10 cm, v katerega je vpisan krog, katerega polmer najti. Najprej najdemo pol-perimeter. V našem problemu bo enaka 11 cm, zdaj pa jo nadomestimo z glavno formulo. Polmer bo enak 1,65 centimetra. Zapišemo odgovor in ne pozabimo na pravilne enote.

Krog in njegove lastnosti

Vsak geometrijska oblika ima svoje značilnosti. Iz njihovega razumevanja je odvisna pravilnost reševanja problemov. Imajo krog. Pogosto se uporabljajo pri reševanju primerov s številkami, ki so opisane ali napisane, saj dajejo jasno predstavo o tej situaciji. Med njimi so:

• Ravna črta ima lahko nič, eno ali dve presečišči s krogom. V prvem primeru se s seboj ne seka, v drugem je tangenta, v tretjem - sekant.
• Če vzamemo tri točke, ki ne ležijo na eni premici, potem lahko skozi njih potegnemo le en krog.
• Ravna črta je lahko tangenta dveh številk hkrati. V tem primeru bo šel skozi točko, ki leži na segmentu, ki povezuje središča krogov. Njegova dolžina je enaka vsoti polmerov teh številk.
• Skozi eno ali dve točki lahko narišete neskončno število krogov.