Kako izračunati površino trikotnika

Trikotnik je dobro znana številka. In to kljub bogati raznolikosti njenih oblik. Pravokotni, enakostranični, akutni, enakostranični, nejasni. Vsak je drugačen. Toda za vsakogar, ki ga potrebujete, morate poznati območje trikotnika.

Skupno za vse trikotnike, ki uporabljajo dolžino strani ali višine

V njih sprejete oznake: stranke - a, b, c; višine na pripadajočih straneh n _in , n _v , n _s .

1. Območje trikotnika je izračunano kot zmnožek ½, strani in višine na njem. S = ½ * a * n _a . Podobno morate napisati formulo za druge dve strani.

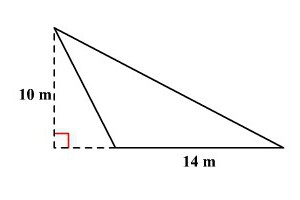
2. Heronova formula, v kateri se pojavi pol-perimeter (običajno je označena z majhno črko p, v nasprotju s celotnim obsegom). Pol-perimeter je treba šteti na naslednji način: skupaj z vsemi stranicami in jih razdelimo na 2. Pol-perimeter formula: p = (a + b + c) / 2. Torej enakost za površino slike izgleda takole: S = √ (p * (p - a) * ( p - c) * (p - c)).

3. Če ne želite uporabiti pol-perimeter, je uporabna formula, v kateri so prisotne le dolžine strani: S = √ * √ (((a + b + c) * (b + c - a) * (a + c - b) * (a + b - c)). To je nekoliko daljše od prejšnjega, vendar bo pomagalo, če ste pozabili najti pol-perimeter.

Splošne formule, v katerih se pojavijo koti trikotnika

Oznake, ki so potrebne za branje formul: α, β, γ - koti. So nasproti stranicam a, b, c.

1. V skladu s tem je polovica produkta dveh strani in sinus kota med njimi enaka površini trikotnika. To je: S = ½ a * b * sin γ. Podobno je treba za druga dva primera navesti formule.

2. Območje trikotnika se lahko izračuna na eni strani in na treh znanih kotih. S = (a ² * sin β * sin γ) / (2 sin α).

3. Obstaja tudi formula z eno dobro znano stranjo in dvema vogali, ki mejijo nanj. Izgleda takole: S = c ² / (2 (ctg α + ctg β)).

Zadnji dve formuli nista najlažji. Zapomni si jih precej težko.

Splošne formule za situacijo, ko so znani polmeri vpisanih ali omejenih krogov.

Dodatne oznake: r, R - polmeri. Prvi se uporablja za polmer vpisanega kroga. Druga je za opisano.

1. Prva formula, s katero se izračuna površina trikotnika, je povezana s pol-perimetrom. S = p * r. Na drug način lahko zapišemo takole: S = ½ r * (a + b + c).

2. V drugem primeru boste morali pomnožiti vse strani trikotnika in jih razdeliti s štirikratnim polmerom krožnice. V dobesednem smislu izgleda tako: S = (a * c * s) / (4R).

3. Tretja situacija vam omogoča, da ne poznate strani, vendar bodo zahtevane vrednosti vseh treh kotov. S = 2 R2 ² sin α * sin β * sin γ.

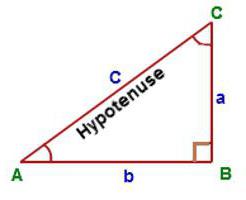
Poseben primer: pravokotni trikotnik

To je najpreprostejša situacija, saj zahteva poznavanje le dolžine obeh nog. Označeni so z latinskimi črkami a in c. Območje pravokotnega trikotnika je enako polovici površine pravokotnika, ki je bil dokončan.

Matematično izgleda tako: S = ½ a * c. Najlažje se ga spomni. Ker izgleda kot formula za območje pravokotnika, se prikaže samo še en del, kar pomeni polovico.

Poseben primer: enakokračni trikotnik

Ker ima dve enaki strani, so nekatere formule za njeno področje nekoliko poenostavljene. Na primer, Heronova formula, ki izračunava območje enakokrakega trikotnika, ima naslednjo obliko:

S = ½ v √ (((+ ½ in) * (a - ½ in)).

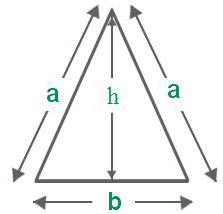
Če ga pretvorite, bo krajši. V tem primeru je Heronova formula za enakokraki trikotnik zapisana kot:

S = v √ (4 * a ² - b ² ).

Nekoliko enostavnejša kot za poljuben trikotnik, izgleda formula za območje, če sta znani strani in kot med njimi. S = ½ a ² * sin β.

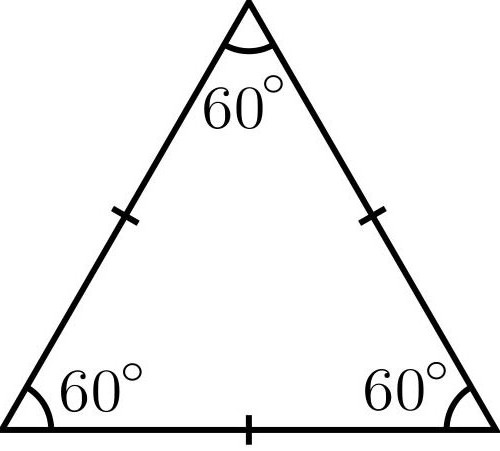
Poseben primer: enakostranični trikotnik

Običajno pri težavah z njim je znana stran ali pa jo lahko nekako ugotovite. Nato formula, ki je območje takšnega trikotnika, izgleda takole:

S = (a ² ) 3) / 4.

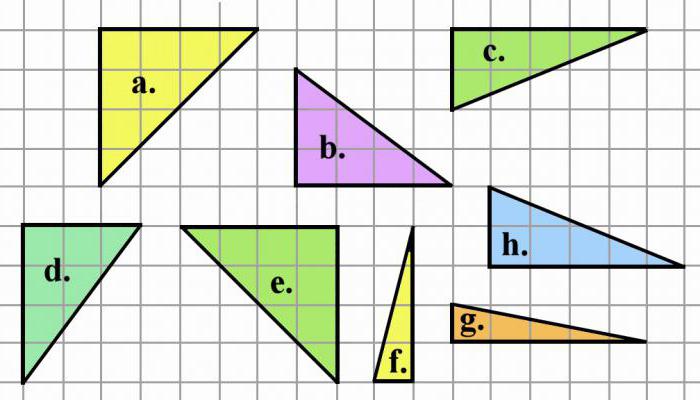
Naloge za iskanje območja, če je trikotnik upodobljen na karirastem papirju

Najenostavnejša je situacija, ko je pravokotni trikotnik narisan tako, da njegove noge sovpadajo s črtami papirja. Potem morate samo prešteti število celic, ki se prilegajo v noge. Nato jih pomnožite in razdelite na dva.

Ko je trikotnik akutno nagnjen ali nejasen, ga je treba narisati do pravokotnika. Potem se v nastali obliki pojavijo trije trikotniki. Ena je tista, ki je podana v problemu. Druga dva - pomožna in pravokotna. Določite območje zadnjih dveh potreb po zgornji metodi. Nato preštejte območje pravokotnika in ga odštejte od tistih, ki so izračunani za pomožno. Območje trikotnika je definirano.

Veliko težje je stanje, v katerem se nobena stran trikotnika ne ujema s črtami papirja. Nato ga je treba vpisati v pravokotnik, tako da so tocke prvotne figure lezene na straneh. V tem primeru bodo trije pomožni desni trikotniki.

Primer problema na formuli Gerone

Stanje Nekateri trikotniki imajo stranice. So enake 3, 5 in 6 cm in morate poznati njeno območje.

Odločitev. Najprej je treba šteti pol-perimeter trikotnika. Naredite vsoto vseh treh, podanih v problemu, številke in jih razdelite na dva dela. Enostavni izračuni vodijo do števila 7. To je vrednost pol metra.

Zdaj lahko izračunate površino trikotnika z uporabo zgornje formule. Pod kvadratni koren Izkazalo se je, da je rezultat štirih števil: 7, 4, 2 in 1. To pomeni, da je območje √ (4 * 14) = 2 √ (14).

Če večja natančnost ni potrebna, lahko izvlečete kvadratni koren iz 14. To je enako 3.74. Nato bo območje enako 7.48.

Odgovor je. S = 2 x 14 cm ² ali 7,48 cm2.

Primer težave s pravim trikotnikom

Stanje Ena noga pravokotnega trikotnika je 31 cm daljša od druge in morate poznati njihove dolžine, če je površina trikotnika 180 cm ² .
Odločitev. Rešiti bomo morali sistem dveh enačb. Prvi je povezan s kvadratom. Drugi je s stališčem nog, ki je podan v problemu.
180 = ½ a * c;

a = pri + 31.
Najprej je treba vrednost "a" nadomestiti s prvo enačbo. Izkazalo se je: 180 = ½ (v + 31) * c. Ima samo eno neznano količino, zato jo je enostavno rešiti. Ko odprete oklepaje, dobimo kvadratno enačbo: v ² + 31 v - 360 = 0. Poda dve vrednosti za "in": 9 in - 40. Drugo število ne ustreza odgovoru, ker dolžina strani trikotnika ne more biti negativna vrednost.

Preostanek za izračun drugega dela: dodamo 31 k dobljenemu številu Izkazalo se je, da je 40. To so količine, ki se iščejo v problemu.

Odgovor je. Noge trikotnika so 9 in 40 cm.

Naloga, da najde stran skozi območje, stran in kot trikotnika

Stanje Površina trikotnika je 60 cm2. Izračunati je treba eno od njenih strani, če je druga stran 15 cm, kot med njimi pa 30º.

Odločitev. Na podlagi sprejetega zapisa je želena stran "a", znana "v", podan kot "γ". Nato lahko formulo za območje prepišemo kot:

60 = ½ a * 15 * sin 30 °. Tu je sinus 30 stopinj 0,5.

Po transformaciji je "a" enaka 60 / (0.5 * 0.5 * 15). To je 16.

Odgovor je. Potrebna stran je 16 cm.

Problem kvadrata, vpisanega v pravokotni trikotnik

Stanje Zgornji del kvadrata s stranico 24 cm se ujema s pravim kotom trikotnika. Druga dva ležita na nogah. Tretji pripada hipotenuze. Dolžina ene od nog je 42 cm. Kakšna je površina pravokotnega trikotnika?

Odločitev. Razmislite o dveh pravih trikotnikih. Prvi je podan v nalogi. Drugi temelji na znani legi prvotnega trikotnika. Podobne so, saj imajo skupen kot in jih tvorijo vzporedne črte.

Potem so odnosi njihovih nog enaki. Noge manjšega trikotnika so 24 cm (stran kvadrata) in 18 cm (stran 42 cm odštejemo stran kvadrata). Ustrezni kraki velikega trikotnika so 42 cm in x cm, zato je ta »x« potreben za izračun površine trikotnika.

18/42 = 24 / x, t.j. x = 24 * 42/18 = 56 (cm).

Nato je območje enako izdelku 56 in 42, razdeljeno na dva dela, to je 1176 cm ² .

Odgovor je. Zahtevana površina je 1176 cm ² .