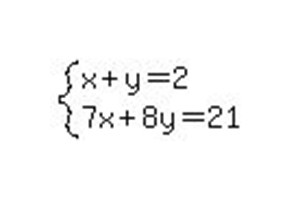Gaussova metoda za reševanje matrik. Rešitev sistema linearnih enačb po Gaussovi metodi

Od začetka XVI-XVIII stoletja so matematiki začeli intenzivno preučevati funkcije, zaradi katerih se je v našem življenju spremenilo toliko stvari. Računalniška tehnologija brez tega znanja preprosto ne bi obstajala. Za reševanje kompleksnih problemov, linearnih enačb in funkcij, so nastali različni koncepti, izreki in metode reševanja. Ena od takih univerzalnih in racionalnih metod in metod za reševanje linearnih enačb in njihovih sistemov je bila Gaussova metoda. Matrike, njihov rang, determinanta - vse je mogoče izračunati brez uporabe kompleksnih operacij.

Kaj je slau

V matematiki je koncept SLAE - sistem linearnih algebrskih enačb. Kakšna je? To je množica m enačb z neznanimi spremenljivkami n neznanimi, običajno označenimi kot x, y, z ali x ₁ , x ₂ ... x _n ali drugimi simboli. Rešitev tega sistema z uporabo Gaussove metode pomeni najti vse neznane neznanke. Če ima sistem enako število neznanih in enačb, se imenuje sistem n-tega reda.

Najbolj priljubljene metode za reševanje klanja

V izobraževalnih ustanovah srednjega izobraževanja preučujejo različne metode reševanja takšnih sistemov. Najpogosteje so to preproste enačbe, ki so sestavljene iz dveh neznank, tako da nobena obstoječa metoda za iskanje odgovora nanje ne bo trajala dolgo. To je lahko metoda zamenjave, kadar druga izhaja iz ene enačbe in se nadomesti z izvirno. Ali metoda izraza z odštevanjem in dodajanjem. Vendar je Gaussova metoda najlažja in univerzalna. Omogoča reševanje enačb s poljubnim številom neznank. Zakaj je ta tehnika razumna? Preprosto je. Metoda matrice je dobra, ker ni potrebno večkrat prepisovati nepotrebnih znakov kot neznane, dovolj je opraviti aritmetične operacije na koeficientih - in dobite zanesljiv rezultat.

Kje se v praksi uporabljajo SLAE

Rešitev SLAE je presečišče točk na grafih funkcij. V naši visokotehnološki računalniški dobi morajo ljudje, ki so tesno povezani z razvojem iger in drugih programov, vedeti, kako rešiti takšne sisteme, kaj predstavljajo in kako preveriti pravilnost dobljenega rezultata. Najpogosteje programerji razvijajo posebne računalniške programe za linearno algebro, kar vključuje sistem linearnih enačb. Gaussova metoda omogoča izračun vseh obstoječih rešitev. Uporabljajo se tudi druge poenostavljene formule in tehnike.

Merilo združljivosti SLAU

Tak sistem je mogoče rešiti le, če je združljiv. Zaradi jasnosti predstavljamo SLAE kot Ax = b. Ima rešitev, če je rang (A) enak rangu (A, b). V tem primeru je (A, b) matrika razširjenega tipa, ki jo lahko dobimo iz matrike A tako, da jo prepišemo s prostimi člani. Izkazalo se je, da rešite linearne enačbe Gaussova metoda je precej enostavna.

Morda nekaj notacije ni povsem jasno, zato morate vse zgledati z zgledom. Recimo, da obstaja sistem: x + y = 1; 2x-3y = 6. Sestavljen je iz samo dveh enačb, v katerih sta 2 neznani. Sistem bo imel rešitev le, če je rang njegove matrike enak rangu razširjene matrike. Kaj je rang? To je število neodvisnih linij sistema. V našem primeru je rang matrike 2. Matrica A bo sestavljena iz koeficientov, ki se nahajajo v bližini neznank, koeficienti za znakom "=" pa se prav tako ujemajo z razširjeno matriko.

Zakaj lahko SLAE predstavimo v matrični obliki

Na podlagi merila združljivosti po dokazanem Kronecker-Capellijevem izreku lahko sistem linearnih algebrskih enačb predstavimo v matrični obliki. Z uporabo Gaussove kaskadne metode lahko rešimo matrico in dobimo edini zanesljiv odgovor na celoten sistem. Če je rang navadne matrike enak rangu njegove razširjene matrike, vendar je manjši od števila neznank, potem ima sistem neskončno število odgovorov.

Matrične transformacije

Preden začnemo z reševanjem matrik, moramo vedeti, katere akcije se lahko izvajajo na njihovih elementih. Obstaja več osnovnih sprememb:

• S ponovnim zapisovanjem sistema v matrični pogled in implementacijo njegove rešitve je možno pomnožiti vse elemente vrstice z istim koeficientom.
• Da bi matrico pretvorili v kanonsko obliko, lahko zamenjamo dve vzporedni vrsti. Kanonična oblika pomeni, da vsi elementi matrike, ki se nahajajo na glavni diagonali, postanejo enote, preostale pa so ničle.
• Ustrezni elementi vzporednih vrstic matrike se lahko dodajo drug drugemu.

Jordan-Gaussova metoda

Bistvo reševanja sistemov linearnih homogenih in nehomogenih enačb z Gaussovo metodo je postopno odpravljanje neznank. Recimo, da imamo sistem iz dveh enačb, v katerih sta dve neznanci. Če jih želite najti, morate preveriti združljivost sistema. Enačba po Gaussovi metodi je rešena zelo preprosto. Potrebno je zapisati koeficiente, ki se nahajajo v bližini vsakega neznanega v pogledu matrike. Za rešitev sistema boste morali zapisati razširjeno matrico. Če ena od enačb vsebuje manjše število neznank, potem je treba na mesto manjkajočega elementa postaviti "0". Na matriko se uporabljajo vse znane metode preoblikovanja: množenje, delitev s številom, dodajanje ustreznih elementov vrstic drug drugemu in druge. Izkazalo se je, da je treba v vsaki vrstici pustiti eno spremenljivko z vrednostjo "1", ostalo pa v ničelni obliki. Za natančnejše razumevanje je treba upoštevati Gaussovo metodo s primeri.

Preprost primer sistemske rešitve 2x2.

Najprej vzamemo preprost sistem algebrskih enačb, v katerem bo 2 neznanci.

Ponovno ga napišite v razširjeno matrico.

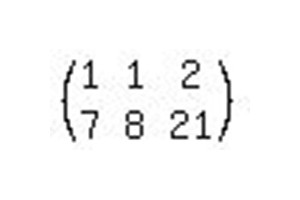
Da bi rešili ta sistem linearnih enačb, je potrebno narediti le dve operaciji. Matrico moramo pripeljati v kanonsko obliko, tako da enote stojijo vzdolž glavne diagonale. Torej, s prenosom matričnega pogleda nazaj na sistem, dobimo enačbe: 1x + 0y = b1 in 0x + 1y = b2, kjer sta b1 in b2 dobljeni odgovori v postopku reševanja.

1. Prvi korak pri reševanju razširjene matrike bi bil: prva vrstica mora biti pomnožena z -7 in pripadajoči elementi dodani drugi vrstici, da se znebimo ene neznane v drugi enačbi.
2. Ker rešitev enačb po Gaussovi metodi pomeni redukcijo matrike na kanonsko obliko, je potrebno opraviti enake operacije s prvo enačbo in odstraniti drugo spremenljivko. Da bi to naredili, drugo vrstico odštejemo od prve in dobimo potreben odgovor - rešitev SLAU. Ali pa, kot je prikazano na sliki, se druga vrstica pomnoži s koeficientom -1 in elementi druge vrstice se dodajo prvi vrstici. To je ista stvar.

Kot lahko vidite, je naš sistem rešen z Jordan-Gaussovo metodo. Ponovno ga prepišemo v zahtevano obliko: x = -5, y = 7.

Primer rešitve 3x3 SLAE

Recimo, da imamo bolj kompleksen sistem linearnih enačb. Gaussova metoda omogoča izračun odgovora tudi za na videz zmeden sam sistem. Zato, da bi dobili globlji vpogled v računsko metodo, se lahko premaknemo na bolj zapleten primer s tremi neznankami.

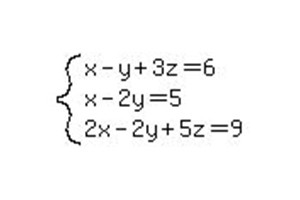
Kot v prejšnjem primeru sistem prepišemo v obliki razširjene matrike in jo začnemo zmanjševati v kanonsko obliko.

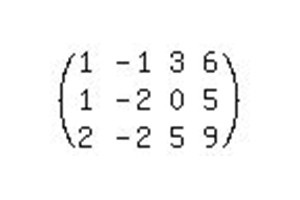
Da bi rešili ta sistem, boste morali narediti veliko več korakov kot v prejšnjem primeru.

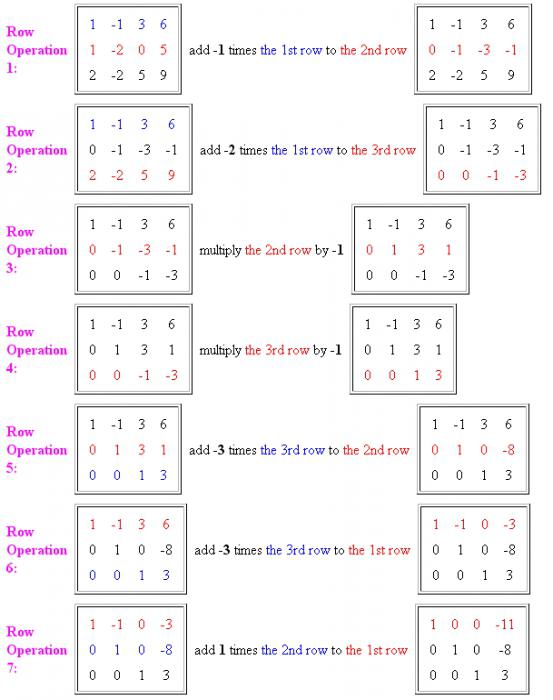
1. Najprej morate v prvem stolpcu narediti en element enote in preostale ničle. To naredite tako, da prvo enačbo pomnožite s -1 in ji dodate drugo enačbo. Pomembno je vedeti, da prvo vrstico prepišemo v prvotni obliki, drugo pa v spremenjeni.
2. Nato odstranite isto prvo neznano iz tretje enačbe. V ta namen se elementi prve vrstice pomnožijo z -2 in jih dodajo v tretjo vrstico. Zdaj sta prva in druga vrstica napisani v izvirni obliki, tretja pa že s spremembami. Kot je razvidno iz rezultata, smo dobili prvo enoto na začetku glavne diagonale matrike in preostale ničle. Nekaj ​​več dejanj in sistem enačb z uporabo Gaussove metode bo zanesljivo rešen.
3. Zdaj je potrebno izvesti operacije na drugih elementih vrstic. Tretji in četrti ukrep se lahko združita v eno. Drugo in tretjo vrstico je potrebno razdeliti s -1, da se diagonalno znebimo negativnih enot. Tretja vrstica je že privedla do potrebne oblike.
4. Sledi druga vrstica v kanonsko obliko. Da bi to naredili, elemente tretje vrstice pomnožimo s -3 in jih dodamo drugi vrstici matrike. Rezultat kaže, da je tudi druga vrstica zmanjšana na obliko, ki jo potrebujemo. Ostaja še nekaj operacij in odstrani koeficiente neznank iz prve vrstice.
5. Da bi iz drugega elementa linije naredili 0, je treba tretjo vrstico pomnožiti s -3 in jo dodati v prvo vrstico.
6. V naslednjem ključnem koraku bomo v prvi vrstici dodali potrebne elemente druge vrstice. Tako dobimo kanonsko obliko matrike in s tem odgovor.

Kot lahko vidite, je rešitev enačb po Gaussovi metodi dokaj preprosta.

Primer reševanja sistema enačb 4x4

Nekatere bolj zapletene sisteme enačb lahko rešimo z Gaussovo metodo s pomočjo računalniških programov. V obstoječe prazne celice je potrebno voziti koeficiente z neznankami, sam program pa bo korak za korakom izračunal potreben rezultat, podrobno opisal vsako dejanje.

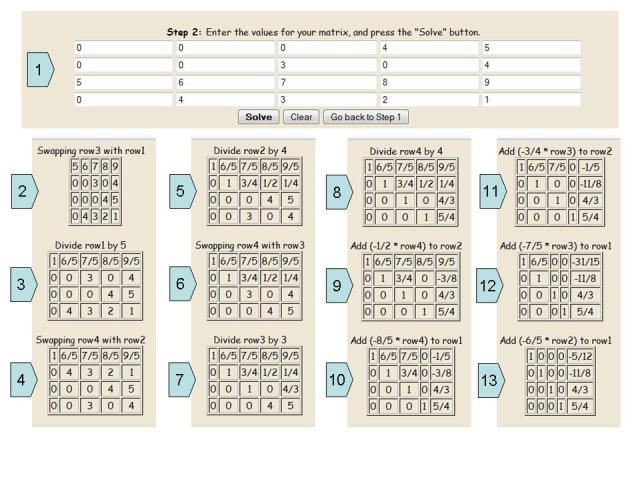
Spodaj je korak za korakom navodila za reševanje takšnega primera.

• V prvem koraku se prosti koeficienti in številke z neznanimi vrednostmi ujemajo s praznimi celicami. Tako se izkaže ista razširjena matrika, ki jo pišemo ročno.

• Nato se vse vrstice obrnejo, tako da se elementi elementov lahko izrazijo vzdolž glavne diagonale.

• In vse potrebne aritmetične operacije se izvajajo, da bi razširjeno matrico pripeljali v kanonsko obliko. Razumeti je treba, da odgovor na sistem enačb ni vedno enak - so cela števila. Včasih je rešitev lahko iz frakcijskih števil.

Rešitev za preverjanje veljavnosti

Jordanovsko-Gaussova metoda omogoča preverjanje pravilnosti rezultata. Da bi ugotovili, ali so koeficienti pravilno izračunani, je potrebno le rezultat nadomestiti z izvirnim sistemom enačb. Leva stran enačbe mora ustrezati desni strani, ki je za enakim znakom. Če se odgovori ne ujemajo, potem morate preračunati sistem ali poskusiti uporabiti drugo metodo reševanja znanega SLAE, kot je substitucija ali termično odštevanje in dodajanje. Navsezadnje je matematika znanost, ki ima veliko različnih tehnik reševanja. Toda ne pozabite: rezultat mora biti vedno enak, ne glede na to, katero metodo ste uporabili.

Gaussova metoda: najpogostejše napake pri reševanju SLAE

Pri reševanju linearnih sistemov enačb se najpogosteje pojavljajo napake, kot je napačen prenos koeficientov na matrično obliko. Obstajajo sistemi, v katerih v eni od enačb ni nekaterih neznank, nato pa se lahko podatki prenesejo v razširjeno matrico in se lahko izgubijo. Posledično pri reševanju tega sistema rezultat morda ne ustreza pravemu.

Še ena od glavnih napak je lahko napačno zapisovanje končnega rezultata. Treba je jasno razumeti, da bo prvi koeficient ustrezal prvemu neznanemu iz sistema, drugemu drugemu in tako naprej.

Gaussova metoda podrobno opisuje rešitev linearnih enačb. Zahvaljujoč njemu je enostavno opraviti potrebne operacije in najti pravi rezultat. Poleg tega je univerzalno orodje za iskanje zanesljivega odgovora na enačbe vseh zapletenosti. Morda se zato pogosto uporablja pri reševanju SLAE.