Poiščite obod trikotnika na različne načine.
Obod vsakega trikotnika je dolžina črte, ki omejuje obliko. Če ga želite izračunati, morate poznati vsoto vseh strani tega poligona.
Izračun iz teh stranskih dolžin
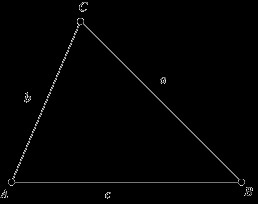
Ko je njihov pomen znan, je to enostavno. Če te parametre označimo s črkami m, n, k in obodom s črko P, dobimo formulo za izračun: P = m + n + k. Naloga: Znano je, da ima trikotnik stranice dolžine 13,5 decimetra, 12,1 decimetra in 4,2 decimetra. Ugotovite območje. Rešimo: Če so stranice danega poligona a = 13,5 dm, b = 12,1 dm, c = 4,2 dm, potem P = 29,8 dm. Odgovor: P = 29,8 dm.
Obod trikotnika, ki ima dve enaki strani
Tak trikotnik se imenuje enakokraki. Če so te enake strani dolge ene centimetre, tretja pa b centimetrov dolge, potem je obrobje enostavno prepoznati: P = b + 2a. Naloga: trikotnik ima dve ploskvi 10 decimetrov, osnova pa je 12 decimetrov. Poišči P. Rešitev: Naj bo stran a = c = 10 dm, osnova b = 12 dm. Vsota strani je P = 10 dm + 12 dm + 10 dm = 32 dm. Odgovor: P = 32 decimeter.
Obod enakostraničnega trikotnika

Če imajo vse tri strani trikotnika enako število enot, se imenuje enakostranični. Drugo ime je pravilno. Območje pravilnega trikotnika najdemo po formuli: P = a + a + a = 3 · a. Naloga: Imamo enakostransko trikotno zemljišče. Ena stran je 6 metrov. Poiščite dolžino ograje, ki lahko obdaja to območje. Rešitev: Če je stran tega poligona a = 6m, je dolžina ograje P = 3,6 = 18 (m). Odgovor: P = 18 m.
Trikotnik s kotom 90 °
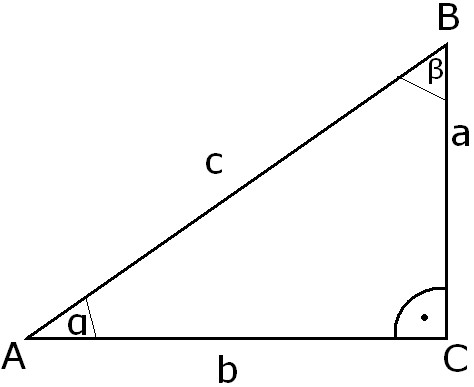
Imenuje se pravokotna. Prisotnost pravega kota omogoča iskanje neznanih strani z definicijo trigonometričnih funkcij in Pitagorejevega izreka. Najdaljša stran se imenuje hipotenuza in je označena s c. Obstajata še dve strani, a in b. Po teoremu, ki nosi ime Pitagora, imamo c 2 = a 2 + b 2 . Noge so a = √ (c 2 - b 2 ) in b = √ (c 2 - a 2 ). Če poznamo dolžino dveh nog a in b, izračunamo hipotenuzo. Nato najdemo vsoto strani slike, ki dodajo te vrednosti. Iskanje: Cateta pravokotni trikotnik dolžine 8,3 cm in 6,2 cm. Obseg trikotnika je treba izračunati. Rešimo: Označujemo noge a = 8,3 cm, b = 6,2 cm, po pitagorejevem izreku je hipotenuza c = √ (8,3 2 + 6,2 2 ) = √ (68,89 + 38,44) = 7107 33 = 10,4 (cm). P = 24,9 (cm). Ali P = 8,3 + 6,2 + √ (8,3 2 + 6,2 2 ) = 24,9 (cm). Odgovor: P = 24,9 cm, vrednosti korenin pa desetino. Če poznamo vrednosti hipotenuze in noge, se vrednost P izračuna z izračunom P = √ (c 2 - b 2 ) + b + c. Naloga 2: Kos zemljišča, ki leži nasproti kota 90 stopinj, 12 km, ena od nog - 8 km. Koliko časa lahko hodite po celotnem območju, če se premikate s hitrostjo 4 kilometre na uro? Rešitev: če je največji segment 12 km, manj kot b = 8 km, bo dolžina celotne poti P = 8 + 12 + √ (12 2 - 8 2 ) = 20 + =80 = 20 + 8.9 = 28.9 ( km). Našli bomo čas z delitvijo poti s hitrostjo. 28,9: 4 = 7,225 (h). Odgovor: lahko dobite okoli 7,3 ure kvadratne korenine in odgovor vzamemo do desetine. Zbirko stranic pravokotnega trikotnika lahko najdete, če je podana ena od strani in vrednost enega od ostrih vogalov. Če poznamo dolžino noge b in vrednost nasprotnega kota β, najdemo neznano stran a = b / tg β. Najdi hipotenuzo c = a: sinα. Obseg takšne številke najdemo z dodajanjem dobljenih vrednosti. P = a + a / sinα + a / tg α ali P = a (1 / sin α + 1 + 1 / tg α). Naloga: V pravokotnem Δ АВС s pravim kotom C so sončne noge dolge 10 m, kot A pa 29 stopinj. Treba je najti vsoto strank Δ АВС. Rešitev: Označimo znano nogo BC = a = 10 m, kot nasproti ležečemu kotu, =A = α = 30 °, nato pa nogo AC = b = 10: 0.58 = 17.2 (m), hipotenuzo AB = c = 10: 0,5 = 20 (m). P = 10 + 17,2 + 20 = 47,2 (m). Ali P = 10 · (1 + 1.72 + 2) = 47.2 m. Imamo: P = 47.2 m. Vrednost trigonometričnih funkcij vzamemo s točnostjo ene stotine, dolžino stranic in oboda pa zaokrožimo na deseto. Z vrednostjo nožice α in sosednjega kota β ugotovimo, kaj je drugi krak enak: b = a tan β. Hipotenuza bo v tem primeru enaka nogi, ki jo delimo s kosinusom kota β. Obod je znan po formuli P = a + a tg β + a: cos β = (tg β + 1 + 1: cos β) · a. Naloga: Noga trikotnika s kotom 90 stopinj 18 cm, sosednji kot je 40 stopinj. Poišči P. Rešitev: Označimo znano nogo BC = 18 cm, ∟β = 40 °. Potem je neznana noga AC = b = 18 · 0.83 = 14.9 (cm), hipotenuza AB = c = 18: 0.77 = 23.4 (cm). Vsota strani je enaka R = 56,3 (cm). Ali P = (1 + 1,3 + 0,83) * 18 = 56,3 cm Odgovor: P = 56,3 cm. Če je znana dolžina hipotenuze c in katerikoli kot α, bodo noge enake zmnožku hipotenuze za prvi - na sinusu in za drugi - na kosinus tega kota. Obseg te številke je P = (sin α + 1 + cos α) * c. Naloga: Hypotenuse pravokotnega trikotnika AB = 9,1 cm in kota 50 stopinj. Poišči vsoto strani te številke. Rešitev: Določimo hipotenuzo: AB = c = 9,1 cm, =A = α = 50 °, potem ima ena od BC nog dolžino a = 9,1 · 0,77 = 7 (cm), ACH = b = 9 1, 0.64 = 5.8 (cm). Tako je obseg tega poligona P = 9,1 + 7 + 5,8 = 21,9 (cm). Ali P = 9,1 · (1 + 0,77 + 0,64) = 21,9 (cm). Odgovor: P = 21,9 centimetrov.
Poljuben trikotnik, katerega ena stran je neznana
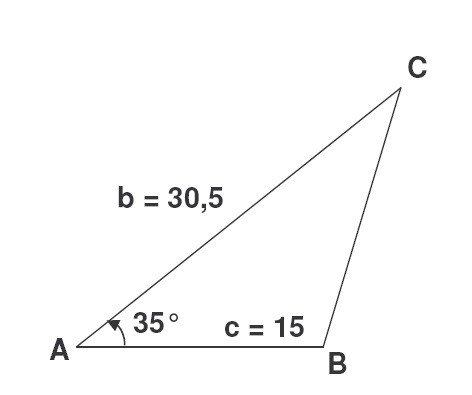
Če imamo vrednosti dveh strani a in c, kot med temi stranicami pa je γ, najdemo tretji kosinusni izrek: b 2 = s 2 + a 2 - 2 as cos β, kjer je β kot med stranema a in c. Potem bomo našli obod. Naloga: Δ АВС ima segment AB dolžine 15 dm, segment AC, katerega dolžina je 30,5 dm. Kot med temi stranicami je 35 stopinj. Izračunajte vsoto strank Δ ABC. Rešitev: Cosineov izrek izračunajte dolžino tretje osebe. BC 2 = 30,5 2 + 15 2 - 2 · 30,5 · 15 · 0,82 = 930,25 + 225 - 750,3 = 404,95. BC = 20,1 cm P = 30,5 + 15 + 20,1 = 65,6 (dm): P = 65,6 dm.
Vsota strani poljubnega trikotnika, katerih dolžine na obeh straneh so neznane

Če poznamo dolžino samo enega segmenta in vrednost dveh kotov, lahko z uporabo sinusnega izreka ugotovimo dolžino dveh neznanih strani: »v trikotniku so stranice vedno sorazmerne s sinusnim vrednostim nasprotnih vogalov«. Kjer je b = (a * sin β) / sin a. Podobno je c = (sin γ): sin a. Območje v tem primeru bo P = a + (sin β) / sin a + (sin γ) / sin a. Naloga: Imamo Δ ABC. V njej je dolžina stranice BC 8,5 mm, vrednost kota C je 47 °, kot B pa 35 stopinj. Poišči vsoto strani te številke. Rešitev: Označimo dolžine strani BC = a = 8,5 mm, AC = b, AB = c, = A = α = 47 °, =B = β = 35 °, = C = γ = 180 ° - (47 ° + 35 °) = 180 ° - 82 ° = 98 °. Iz relacij, ki izhajajo iz sinusnega izreka, najdemo noge AC = b = (8,5 · 0,57): 0,73 = 6,7 (mm), AB = c = (7 · 0,99): 0,73 = 9,5 (mm). Zato je vsota strani tega poligona P = 8,5 mm + 5,5 mm + 9,5 mm = 23,5 mm. Odgovor: P = 23,5 mm. V primeru, da obstaja le dolžina enega segmenta in vrednosti dveh sosednjih kotov, najprej izračunamo kot nasproti znani strani. Vsi vogali te številke imajo skupaj 180 stopinj. Zato je =A = 180 ° - (+B + )C). Nato najdemo neznane segmente z uporabo sinusnega izreka. Naloga: Imamo Δ ABC. Ima segment BC, ki je enak 10 cm, kot B pa 48 stopinj, kot C je 56 stopinj. Poišči vsoto strank Δ abc. Rešitev: Najprej poiščite vrednost kota A, nasproti strani BC. =A = 180 ° - (48 ° + 56 °) = 76 °. Zdaj s sinusnim izrekom izračunamo dolžino strani AC = 10,70: 0,97 = 7,6 (cm). AB = BC * sin C / sin A = 8,6. Obod trikotnika je P = 10 + 8.6 + 7.6 = 26.2 (cm). Rezultat: P = 26,2 cm.
Izračunaj obseg trikotnika s polmerom vtisnjenega kroga
Včasih ni znanih nobenih pogojev problema. Vendar pa obstaja vrednost trikotniško območje in polmer kroga, v katerega je vpisan. Te vrednosti so povezane: S = r p. Poznavanje vrednosti območja trikotnika, polmera r, lahko najdemo pol-perimeter p. Najdi p = S: r. Naloga: Parcela ima površino 24 m 2 , polmer r je 3 m. Če je razdalja med dvema sosednjima 2 metrov, najdejo število dreves, ki jih je treba enakomerno zasaditi ob progi, ki obdaja ta odsek. Rešitev: Vsota strani te številke je na voljo na naslednji način: P = 2, 24: 3 = 16 (m). Nato delite z dvema. 16: 2 = 8. Skupaj: 8 dreves.
Vsota strani trikotnika v pravokotnih koordinatah
Vertice Δ АВС imajo koordinate: A (x 1 ; y 1 ), B (x 2 ; y 2 ), C (x 3 ; y 3 ). Poiščite kvadrate vsake strani AB 2 = (x 1 - x 2 ) 2 + (y 1 - y 2 ) 2 ; BC 2 = (x 2 - x 3 ) 2 + (y 2 - y 3 ) 2 ; AC 2 = (x 1 - x 3 ) 2 + (y 1 - y 3 ) 2 . Da bi našli območje, je dovolj, da dodate vse segmente. Naloga: Vertexne koordinate Δ ABC: B (3; 0), A (1; -3), C (2; 5). Poišči vsoto strani te številke. Rešitev: vstavimo vrednosti ustreznih koordinat v perimetrsko formulo, dobimo P = √ (4 + 9) + √ (1 + 25) + √ (1 + 64) = +13 + +26 + √65 = 3.6 + 5.1 + 8,0 = 16,6. Imamo: P = 16,6. Če številka ni na ravnini, ampak v prostoru, ima vsaka od tock tri koordinate. Zato bo vsota strank imela še en mandat.
Vektorska metoda
Če je oblika podana s koordinatami tock, se lahko obmocje izracuna z vektorsko metodo. Vektor je segment, ki ima smer. Njegov modul (dolžina) je označen s simbolom. Razdalja med točkami je dolžina ustreznega vektorja ali modul vektorja. Razmislite o trikotniku, ki leži na ravnini. Če imajo točke imajo koordinate A (x 1 ; y 1 ), M (x 2 ; y 2 ), T (x 3 ; y 3 ), se dolžina vsake strani po formuli nahaja: AM = √ ((x 1 - x 2) ) 2 + (y 1 - y 2 ) 2 ), ǀMTǀ = √ ((x 2 - x 3 ) 2 + (y 2 - y 3 ) 2 ), ǀATǀ = √ ((x 1 - x 3 ) 2 + ( 1 - 3 ) 2 ). Območje trikotnika je dobljeno z dodajanjem dolžin vektorjev. Podobno najdemo vsoto strani trikotnika v prostoru.