Fibonaccijevo zaporedje in načela zlatega odseka
Fibonaccijevo zaporedje, ki je postalo znano večini skozi film in knjigo Da Vincijeve kode, je serija številk, ki jih je v trinajstem stoletju izvedel italijanski matematik Leonardo iz Pise, bolj znan po psevdonimu Fibonacci. Sledilci znanstvenika so opazili, da formula, v kateri je ta serija številk podrejena, najde svoj odsev v svetu okoli nas in odmeva z drugimi matematičnimi odkritji, s čimer nam odpira vrata za skrivnosti vesolja. V tem članku bomo opisali, kaj je Fibonaccijevo zaporedje, razmisliti o primerih kartiranja tega vzorca v naravi in ga primerjati z drugimi matematičnimi teorijami. 
Oblikovanje in definicija
Fibonaccijev niz je matematično zaporedje, katerega vsak element je enak vsoti prejšnjih dveh. Naj bo neka članica zaporedja xn. Tako dobimo formulo, ki velja za celotno serijo: xn + 2 = xn + xn + 1. S tem zaporedja bo izgledal takole: 1, 1, 2, 3, 5, 8, 13, 21, 34. Naslednja številka bo 55, saj je vsota 21 in 34 55. In tako naprej po istem načelu.
Ad
Primeri v okolju
Če pogledamo rastlino, zlasti na krono listov, ugotavljamo, da cvetijo v spirali. Koti se oblikujejo med sosednjimi listi, ki tvorijo pravilen matematični Fibonacci. Zahvaljujoč tej funkciji vsak list, ki raste na drevesu, prejme največjo količino sončne svetlobe in toplote. 
Fibonacci matematični puzzle
Slavni matematik je predstavil svojo teorijo kot uganko. Sliši se tako. Par zajcev lahko postavite v zaprt prostor, da bi ugotovili, koliko pari zajcev se bo rodilo v enem letu. Glede na naravo teh živali, dejstvo, da vsak mesec par je sposoben proizvajati nov par, in so pripravljeni za vzrejo po doseganju dveh mesecev, na koncu je prejel svojo slavno število številk: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144 - kjer je prikazano število novih parov kuncev v vsakem mesecu.
Ad
Fibonaccijevo zaporedje in proporcionalno razmerje
Ta serija ima več matematičnih odtenkov, ki jih morate vsekakor upoštevati. On, ki se približuje počasneje in počasneje (asimptotično), se nagiba k sorazmernemu razmerju. Ampak to je nerazumno. Z drugimi besedami, to je število z nepredvidljivim in neskončnim zaporedjem decimalnih števil v frakcijskem delu. Na primer, razmerje med katerim koli elementom serije se giblje okrog številke 1.618, nato pa presega, nato pa doseže. Po analogiji se približuje 0,618. Kar je obratno sorazmerno s številom 1.618. Če elemente razdelimo skozi eno, dobimo 2.618 in 0.382. Kot ste že razumeli, so tudi obratno sorazmerni. Nastale številke se imenujejo Fibonaccijevi koeficienti. In zdaj bomo pojasnili, zakaj smo izvedli te izračune. 
Zlato razmerje
Vse predmete okoli nas ločimo po določenih merilih. Ena od njih je oblika. Nekateri od nas privabljajo več, nekateri manj, nekateri pa ne. Opaziti je, da človek lažje zazna simetrični in proporcionalni objekt in povzroči občutek harmonije in lepote. Celotna slika vedno vključuje dele različnih velikosti, ki so v določenem razmerju med seboj. Zato je odgovor na vprašanje, kaj se imenuje Zlati del. Ta koncept pomeni popolnost odnosa med celoto in deli v naravi, znanosti, umetnosti in Z matematičnega vidika upoštevajte naslednji primer. Vzemite odsek poljubne dolžine in ga razdelite na dva dela, tako da se manjši del nanaša na večje kot na vsoto (dolžino celotnega segmenta) na večjega. Torej vzamemo segment c za vrednost enega. Njegov del a bo enak 0,618, drugi del b pa se izkaže, da je enak 0,382. Tako se držimo pogoja Zlati del. Razmerje med segmentom c in a je enako 1,618. Razmerje med deli c in b pa je 2.618. Dobimo Fibonaccijeve koeficiente, ki so nam že znani. Po istem načelu so zgrajeni zlati trikotnik, zlati pravokotnik in zlati kvader. Prav tako je treba omeniti, da je sorazmerno razmerje med deli človeškega telesa blizu Zlato razmerje. 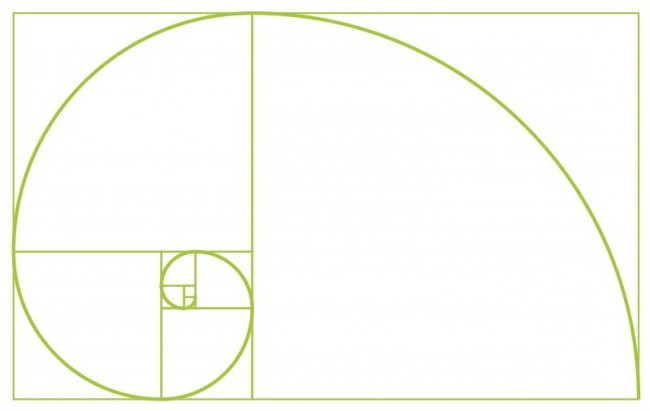
Ali je Fibonaccijevo zaporedje osnova za vse?
Poskusimo združiti teorijo zlatega odseka in znane serije italijanskih matematikov. Začnimo z dvema kvadratoma prve velikosti. Nato na vrh dodamo še en kvadrat druge velikosti. Risnimo zraven iste številke s stransko dolžino, ki je enaka vsoti dveh prejšnjih strani. Podobno narišite kvadrat pete velikosti. In tako lahko nadaljujete v nedogled, dokler vam ne postane dolgčas. Glavna stvar je, da je velikost strani vsakega naslednjega kvadrata enaka vsoti vrednosti strani obeh prejšnjih. Dobimo vrsto poligonov, katerih dolžina je Fibonaccijeva števila. Te številke se imenujejo Fibonaccijevi pravokotniki. Narišemo gladko črto skozi vogale naših poligonov in dobimo ... Arhimedovo spiralo! Povečanje smeri te številke, kot veste, je vedno enotno. Če vklopite domišljijo, lahko nastalo sliko povežete z lupino školjke. Iz tega lahko sklepamo, da je Fibonaccijevo zaporedje osnova proporcionalnih, harmoničnih razmerij elementov v okolju. 
Matematično zaporedje in vesolje
Če pogledate natančno, potem Arhimedovo spiralo (nekje eksplicitno, vendar nekje prikrito) in zato Fibonaccijevo načelo lahko zasledimo v mnogih običajnih naravnih elementih, ki obdajajo človeka. Na primer, isti školjk školjk, florets brokoli, sončnično cvet, stožec iglavcev in podobno. Če pogledamo proč, bomo videli Fibonaccijevo zaporedje v neskončnih galaksijah. Tudi oseba, ki jo navdihuje narava in sprejema njeno obliko, ustvarja predmete, v katerih se sledi omenjeni seriji. Zdaj je čas, da se spomnimo Zlatega oddelka. Skupaj s Fibonaccijevim vzorcem se izsledijo načela te teorije. Obstaja različica, da je Fibonaccijevo zaporedje naravni test, ki se prilagaja bolj popolni in temeljni logaritmični sekvenci zlatega odseka, ki je skoraj identičen, vendar nima začetka in je neskončen. Narava narave je takšna, da mora imeti svojo lastno izhodiščno točko, iz katere se mora graditi, da bi ustvarila nekaj novega. Odnos prvih elementov Fibonaccijevega niza je daleč od načel Zlatega odseka. Vendar, kolikor ga bomo nadaljevali, bolj bo ta neskladnost izravnana. Za določitev zaporedja je potrebno poznati njegove tri elemente, ki sledijo drug drugemu. Za zlato zaporedje je dovolj dve. Ker je oboje aritmetično in geometrijsko napredovanje.
Zaključek
Kljub temu lahko na podlagi zgoraj navedenega zastavite precej logična vprašanja: »Od kod prihajajo te številke? Kdo je avtor celega sveta, ki ga je poskušal narediti popolnega? Kaj se bo zgodilo? Če najdete odgovor na eno vprašanje, dobite naslednje. Rešil sem - še dva se pojavita. Ko jih rešimo, dobiš še tri. Ko jih obravnavate, boste prejeli pet nerešenih vprašanj. Potem osem, nato trinajst, enaindvajset, trideset štiri, petdeset pet ...