Binomska porazdelitev: definicija, formula, primeri
Teorija verjetnosti je nevidno prisotna v našem življenju. Na to ne posvečamo pozornosti, toda vsak dogodek v našem življenju ima določeno verjetnost. Ob upoštevanju velikega števila scenarijev je nujno, da določimo najverjetnejše in najmanj verjetne. Takšne verjetnostne podatke je najbolj primerno grafično analizirati. V tem nam lahko pomaga distribucija. Binomial - eden najlažjih in najbolj natančnih.
Preden se obrnemo neposredno na matematiko in teorijo verjetnosti, se ukvarjamo s tem, kdo je prvi prišel do te vrste distribucije in kakšna je zgodovina razvoja matematičnega aparata za ta koncept.

Zgodovina
Pojem verjetnosti je znan že od antičnih časov. Starodavni matematiki ji niso pripisovali velikega pomena in so lahko postavili samo temelje teorije, ki je kasneje postala teorija verjetnosti. Ustvarili so nekaj kombinatoričnih metod, ki so močno pomagale tistim, ki so kasneje ustvarile in razvile teorijo.
V drugi polovici 17. stoletja se je začelo oblikovanje osnovnih pojmov in metod teorije verjetnosti. Uvedene so definicije naključnih spremenljivk, metode za izračun verjetnosti enostavnih in nekaterih zapletenih neodvisnih in odvisnih dogodkov. Takšno zanimanje za naključne spremenljivke in verjetnosti je narekovalo igre na srečo: vsi so želeli vedeti, kakšne so njegove možnosti za zmago v igri.
Naslednji korak je bila uporaba metod v teoriji verjetnosti matematična analiza. Ugledni matematiki, kot so Laplace, Gauss, Poisson in Bernoulli, so prevzeli to nalogo. To področje matematike so napredovali na novo raven. James Bernoulli je odkril binomski zakon o distribuciji. Mimogrede, kot bomo ugotovili kasneje, je bilo na podlagi tega odkritja izdelanih še nekaj, kar je omogočilo oblikovanje zakona normalne porazdelitve in še veliko več.
Zdaj, preden začnemo opisovati porazdelitev binomskega dela, bomo nekoliko osvežili koncepte teorije verjetnosti, verjetno že pozabljene iz šole.
Osnove teorije verjetnosti
Takšne sisteme bomo obravnavali, zaradi česar so možni le dva izida: "uspeh" in "neuspešnost". To je enostavno razumeti z zgledom: vrgnemo kovanec, da bi uganil, da bodo repi izpadli. Verjetnost vsakega od možnih dogodkov (repi izpadajo - "uspeh", orel pade - "ne uspeh") je 50 odstotkov s popolnim uravnoteženjem kovanca in odsotnostjo drugih dejavnikov, ki bi lahko vplivali na poskus.
To je bil najpreprostejši dogodek. Obstajajo pa tudi kompleksni sistemi, v katerih se izvajajo sekvenčni ukrepi, in verjetnosti rezultatov teh ukrepov se bodo razlikovale. Na primer, razmislite o takem sistemu: v škatli, katere vsebina ne moremo videti, je šest popolnoma enakih kroglic, tri pare modre, rdeče in bele. Moramo dobiti naključno nekaj žogic. V skladu s tem bomo z vlečenjem prve bele kroglice včasih zmanjšali verjetnost, da bo naslednja dobila tudi belo kroglo. To se zgodi, ker se število objektov v sistemu spremeni.
V naslednjem razdelku bomo pogledali bolj zapletene matematične koncepte, ki nas tesno vodijo do tega, kaj besede »normalna porazdelitev«, »binomska porazdelitev« in podobno pomeni.

Elementi matematične statistike
V statistiki, ki je eno od področij uporabe teorije verjetnosti, obstaja veliko primerov, kjer podatki za analizo niso podani izrecno. To pa ni v numeričnem, ampak v obliki delitve po znakih, na primer po spolu. Za uporabo matematičnega aparata za takšne podatke in pridobitev kakršnih koli sklepov iz dobljenih rezultatov je treba pretvoriti izvirne podatke v numerično obliko. Da bi to dosegli, se praviloma pozitivnemu izidu dodeli vrednost 1, negativni izid pa je 0. Tako dobimo statistične podatke, ki jih lahko analiziramo z matematičnimi metodami.
Naslednji korak pri razumevanju, kaj je binomska porazdelitev naključne spremenljivke, je določiti varianco naključne spremenljivke in matematično pričakovanje. To je obravnavano v naslednjem razdelku.
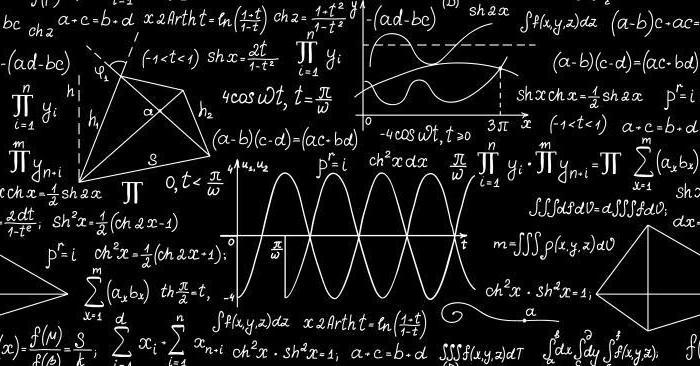
Matematično pričakovanje
Pravzaprav je lahko razumeti, kakšna so pričakovanja. Razmislite o sistemu, v katerem je veliko različnih dogodkov z različnimi verjetnostmi. Matematično pričakovanje se imenuje vrednost, ki je enaka vsoti produktov vrednosti teh dogodkov (in matematične oblike, o kateri smo razpravljali v zadnjem delu) o verjetnosti njihovega izvajanja.
Matematično pričakovanje binomske porazdelitve se izračuna po isti shemi: vzamemo vrednost naključne spremenljivke, jo pomnožimo z verjetnostjo pozitivnega izida, nato pa povzamemo podatke, pridobljene za vse količine. Te podatke je zelo priročno predstaviti grafično - tako se bolje zazna razlika med matematičnimi pričakovanji različnih količin.
V naslednjem razdelku vam bomo povedali nekaj o drugem konceptu - varianci naključne spremenljivke. Prav tako je tesno povezana s takšnim konceptom kot binomska porazdelitev verjetnosti in je njegova značilnost.
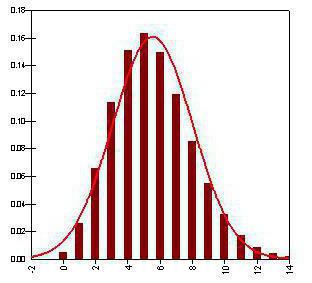
Varianca binomske porazdelitve
Ta vrednost je tesno povezana s prejšnjo in označuje tudi distribucijo statističnih podatkov. Predstavlja povprečni kvadrat odstopanj vrednosti od njihovega pričakovanja. To pomeni, da je varianca naključne spremenljivke vsota kvadratov razlik med vrednostjo naključne spremenljivke in njenim pričakovanjem, pomnožena z verjetnostjo tega dogodka.
Na splošno je to vse, kar moramo vedeti o varianci, da bi razumeli, kaj je binomska porazdelitev verjetnosti. Zdaj pa se neposredno obrnemo na našo glavno temo. Tisto, kar se skriva za tako na videz precej zapleteno frazo "binomsko distribucijsko pravo".
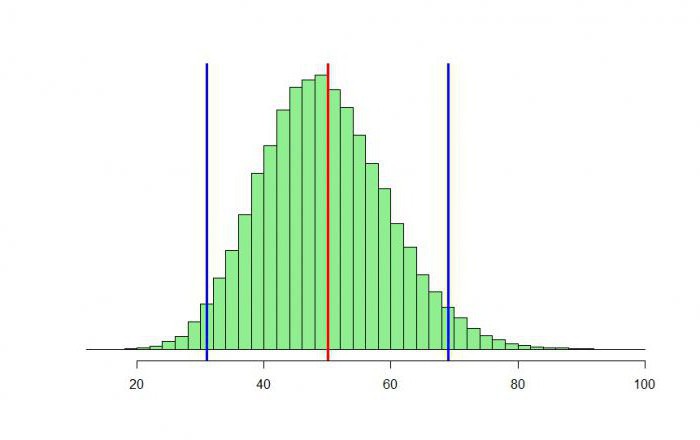
Binomska porazdelitev
Najprej bomo razumeli, zakaj je ta porazdelitev binomska. Prihaja iz besede "bin". Morda ste že slišali za Newtonov binom, formulo, s katero lahko vsoto dveh poljubnih številk a in b razgradimo v katerokoli ne-negativno stopnjo n.
Kot ste verjetno že uganili, sta Newtonova binomska formula in binomska porazdelitvena formula skoraj identične formule. Z edino izjemo, da ima druga uporabno vrednost za določene količine, prva pa je le splošno matematično orodje, katerega uporaba je lahko v praksi različna.
Distribucijske formule
Funkcijo binomske porazdelitve lahko zapišemo kot vsoto naslednjih članov:
(n! / (nk)! k!) * p k * q nk
Tu je n število neodvisnih naključnih eksperimentov, p število uspešnih izidov, q število neuspešnih rezultatov, k je število poskusa (lahko sprejme vrednosti od 0 do n),! - oznaka faktorije, takšna funkcija števila, katere vrednost je enaka zmnožku vseh števil, ki jih doseže (na primer za število 4: 4! = 1 * 2 * 3 * 4 = 24).
Poleg tega lahko binomsko porazdelitveno funkcijo zapišemo kot nepopolno beta funkcijo. Vendar je to bolj zapletena definicija, ki se uporablja le pri reševanju kompleksnih statističnih problemov.
Binomska porazdelitev, primeri, ki smo jih obravnavali zgoraj, je ena najpreprostejših vrst porazdelitev v teoriji verjetnosti. Obstaja tudi normalna porazdelitev, ki je vrsta binomskega. Najpogosteje se uporablja in najbolj preprosto v izračunih. Obstaja tudi Bernoullijeva porazdelitev, Poissonova porazdelitev, pogojna porazdelitev. Vsi grafično označujejo verjetnosti procesa pod različnimi pogoji.
V naslednjem razdelku bomo preučili vidike, povezane z uporabo tega matematičnega aparata v resničnem življenju. Na prvi pogled seveda se zdi, da je to še ena matematična stvar, ki, kot ponavadi, ne najde uporabe v resničnem življenju, in na splošno ni potrebna nikomur, razen samim matematikom. Vendar pa je to daleč od primera. Navsezadnje so bile vse vrste distribucij in njihove grafične podobe ustvarjene izključno za praktične namene, in ne kot muhavost znanstvenikov.
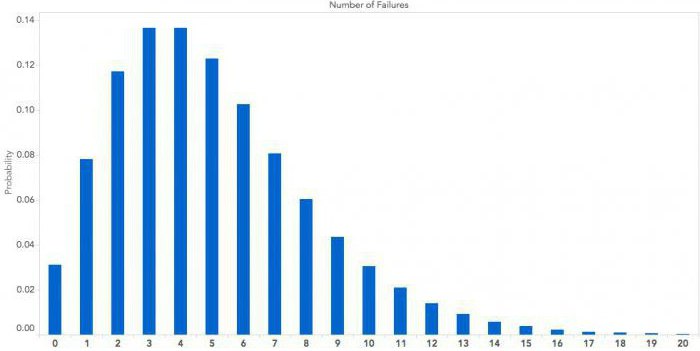
Uporaba
Seveda, najpomembnejša uporaba distribucije najdemo v statistiki, ker potrebujejo celovito analizo niza podatkov. Kot kaže praksa, ima veliko podatkovnih nizov približno enako porazdelitev vrednosti: kritična območja zelo nizkih in zelo visokih vrednosti praviloma vsebujejo manj elementov kot povprečne vrednosti.
Analiza velikih količin podatkov ni potrebna le v statistiki. Nujna je, na primer, v fizični kemiji. V tej znanosti se uporablja za določitev številnih količin, ki so povezane z naključnimi nihanji in gibanji atomov in molekul.
V naslednjem razdelku bomo videli, kako pomembna je uporaba takih statističnih konceptov kot binomska porazdelitev naključne spremenljivke v vsakdanjem življenju za vas in mene.
Zakaj ga potrebujem?
Mnogo ljudi se sprašuje o tem vprašanju, ko gre za matematiko. In mimogrede, matematika se za nič ne imenuje kraljica znanosti. Je osnova fizike, kemije, biologije, ekonomije in v vsaki od teh znanosti se uporablja tudi neka porazdelitev: ali ta diskretna binomska porazdelitev ali normalna ni pomembna. In če podrobneje pogledamo svet okoli nas, bomo videli, da se matematika uporablja povsod: v vsakdanjem življenju, na delovnem mestu in celo v človeških odnosih lahko predstavimo kot statistične podatke in jih analiziramo (mimogrede, tisti, ki delajo v posebne organizacije, ki zbirajo informacije).
Zdaj pa se pogovorimo o tem, kaj storiti, če morate o tej temi vedeti veliko več, kot o tem, kar smo opisali v tem članku.
Kaj še lahko berete?
Informacije, ki smo jih dali v tem članku, še zdaleč niso popolne. Obstaja veliko odtenkov glede oblike, ki jo lahko ima distribucija. Binomska porazdelitev, kot smo že ugotovili, je ena glavnih vrst, na kateri temeljijo vse matematične statistike in teorija verjetnosti.
Če je postalo zanimivo za vas ali v povezavi z vašim delom, morate o tej temi vedeti veliko več, zato boste morali študirati specializirano literaturo. Začeti bi morali z univerzitetnim tečajem matematične analize in iti tja v oddelek teorije verjetnosti. Prav tako bo koristno znanje na področju serije, ker je binomska porazdelitev verjetnosti le niz zaporednih članov.
Zaključek
Preden zaključimo članek, bi radi povedali še eno zanimivo stvar. Nanaša se neposredno na temo našega članka in celotne matematike.
Mnogi ljudje pravijo, da je matematika neuporabna znanost, in ničesar, kar je šlo skozi šolo, jim ni dobro. Toda znanje ni nikoli odveč, in če vam nekaj v življenju ni koristno, to pomeni, da se ga ne spomnite. Če imate znanje, vam lahko pomagajo, če pa jih ni, potem ni treba čakati na pomoč.
Torej smo pogledali koncept binomske porazdelitve in vse sorodne definicije ter govorili o tem, kako to velja za naše življenje.