Vse podrobnosti, kako izračunati površino paralelepipeda

Paralelepiped je najpogostejša številka med ljudmi. Večina prostorov je njegov. Pri popravilu je še posebej pomembno poznati območje paralelepipeda, vsaj njegove stranske ploskve. Konec koncev, morate natančno vedeti, koliko materiala kupiti.

Kakšen je?

To je prizma s štirikotno osnovo. Zato ima štiri stranske ploskve, ki so paralelogrami. To pomeni, da ima takšno telo samo 6 obrazov.

Da bi določili paralelepiped v prostoru, določa območje in prostornino. Prvi je lahko ločeno za vsak obraz in za celotno površino. Poleg tega oddajajo več in samo stranske ploskve.

Kakšne so vrste paralelepipedov?

Nagnjen. Tista, pri kateri stranski obrazi tvorijo kot z osnovo, ki je drugačna od 90 stopinj. Njegovi zgornji in spodnji štirikotniki ne ležijo drug nasproti drugemu, ampak se premikajo.

Neposredno. Paralelepiped, katerega stranske ploskve so pravokotniki, pri podnožju pa slika s poljubnimi koti.

Pravokotna. Poseben primer prejšnjega tipa: v bazi je pravokotnik.

Kocka Poseben tip paralelepipeda, v katerem so vsi obrazi predstavljeni s kvadrati.

Nekatere matematične značilnosti paralelepipeda

Lahko pride do situacije, ko so koristne pri iskanju paralelepipednega območja.

• Robovi, ki ležijo drug proti drugemu, niso le vzporedni, temveč tudi enaki.
• Diagonala paralelepipednega presečišča je razdeljena na enake dele.
• V bolj splošnem primeru, če segment povezuje dve točki na površini telesa in prehaja skozi presečišče diagonal, se ta točka razdeli na polovico.
• Za pravokotni paralelepiped velja enakost, v kateri je v enem delu kvadrat diagonale, v drugem pa vsota kvadratov njegove višine, širine in dolžine.

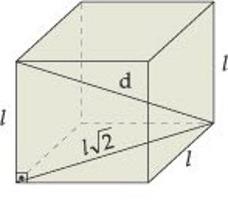
Kvadratni paralelepiped

Če označimo višino telesa kot "n", osnovno perimetro pa s črko "R", potem lahko celotno stransko površino izračunamo po formuli:

S _stran = P _oc * n

Z uporabo te formule in določanjem površine baze lahko izračunamo skupno površino:

S = S _stran + 2 * S _oc

V zadnjem vnosu S _oc ., To je območje osnove paralelepipeda, lahko izračunamo po formuli za paralelogram. Z drugimi besedami, potrebujete izraz, v katerem morate pomnožiti stran in višino, ki jo spustite.

Kvadratni paralelepiped

Sprejeta je standardna oznaka dolžine, širine in višine takega telesa s črkama „a“, „b“ in „c“. Površina bočne površine se izrazi s formulo:

S _stran = 2 * s * (a + b)

Za izračun skupne površine pravokotnega paralelepipeda potrebujemo naslednji izraz:

S = 2 * (aw + bs + kot)

Če se izkaže, da je potrebno poznati območje njegove osnove, je dovolj, da se spomnimo, da je to pravokotnik, kar pomeni, da je dovolj, da pomnožimo "a" in "c".

Kvadratna kocka

Njena stranska površina je sestavljena iz štirih kvadratov. Da bi jo našli, morate uporabiti dobro znano formulo za kvadrat in jo pomnožiti s štirimi.

S _stran = 4 * a ²

Zaradi dejstva, da so njene baze enake kvadrate, se skupna površina določi po formuli:

S = 6 * a ²

Poševni paralelepipedni kvadrati

Ker so njegovi obrazi paralelogrami, morate najti območje vsakega od njih in ga nato zložiti. Na srečo je ravno nasprotno. Zato morate območje izračunati le trikrat, nato pa jih pomnožiti z dvema. Če to napišete v obliki formule, dobite naslednje:

S _stran = (S ₁ + S ₂ ) * 2,

S = (S ₁ + S ₂ + S ₃ ) * 2

Tu sta S ₁ in S ₂ območja dveh stranskih ploskev, S3 pa so osnove.

Povezane naloge

Prva naloga. Stanje Potrebno je vedeti dolžino diagonalna kocka, če je površina celotne površine 200 mm ² .

Odločitev. Začeti moramo s tem, da dobimo izraz za želeno vrednost. Njegov kvadrat je enak trem kvadratom na strani kocke. To pomeni, da je diagonala enaka "a", pomnožena s korenom 3.

Toda stran kocke je neznana. Tukaj boste morali izkoristiti dejstvo, da je celotna površina znana. Iz formule se izkaže, da je "a" enako kvadratni koren iz zasebnih S in 6.

Še vedno ostane le štetje. Rob kocke je √ (200/6), kar je 10 / (3 (mm). Potem bo diagonala enaka (10 / )3) * √3 = 10 (mm).

Odgovor je. Diagram kocke je 10 mm.

Druga naloga. Stanje Potrebno je izračunati površino kocke, če je znano, da je njegov volumen 343 cm2.

Odločitev. Za območje kocke boste morali uporabiti enako formulo. Spet je spet neznan rob telesa. Ampak glede na količino. Iz formule za kocko je zelo enostavno naučiti "a." Enako bo kubični koren 343. Preprost izračun pomeni vrednost za rob: a = 7 cm.

Sedaj je ostalo, da preštejemo kvadrat in ga pomnožimo s 6. a ² = 7 ² = 49, zato bo površina enaka 49 * 6 = 294 (cm2).

Odgovor je. S = 294 cm2.

Tretja naloga. Stanje Podana je pravilna štirikotna prizma z dnom 20 dm. Treba je najti njen stranski rob. Znano je, da je paralelepipedno območje enako 1760 dm ² .

Odločitev. Začnite razmišljati s formulo za območje celotne površine telesa. Samo pri tem je treba upoštevati, da sta robova "a" in "b" enaka. To izhaja iz trditve, da je prizma pravilna. Torej, v njeni bazi je štirikotnik z enakimi stranicami. Zato je a = c = 20 dm.

Glede na te okoliščine je formula za območje poenostavljena na to:

S = 2 * (a ² + 2c).

V njem je vse znano, razen za želeno vrednost "c", ki je ravno stranski rob paralelepipeda. Če jo želite najti, morate izvesti konverzijo:

• vse neenakosti razdelimo na 2;
• nato premaknite izraze tako, da je leva 2as, na desni pa območje, deljeno z 2, in kvadrat "a", ki je označen z "-";
• potem delimo enakost z 2a.

Rezultat je izraz:

c = (s / 2 - a ² ) / (2a)

Po zamenjavi vseh znanih vrednosti in izvedbi dejanj se izkaže, da je stranski rob enak 12 dm.

Odgovor je . Stranski rob "c" je 12 dm.

Četrta naloga. Stanje Glede na pravokotni paralelepiped. Ena od njenih obrazov ima površino 12 cm ² . Potrebno je izračunati dolžino roba, ki je pravokotna na ta obraz. Dodatni pogoj: telesna prostornina je 60 cm ³ .

Odločitev. Naj bo območje tega obraza, ki je obrnjeno proti opazovalcu, znano. Če se za označevanje vzamejo standardne črke za paralelepipedne dimenzije, se na dnu rebra nahajajo “a” in “b”, navpični pa “c”. Na podlagi tega je območje znanega obrazca opredeljeno kot produkt „a“ na „c“.

Zdaj morate uporabiti znani glasnost. Njegova formula za pravokotni paralelepiped daje produkt vseh treh količin: "a", "in" in "c". To pomeni, da znano območje, pomnoženo z "in", daje volumen. Iz tega se izkaže, da se želeni rob izračuna iz enačbe:

12 * = 60.

Elementarni izračun daje rezultat 5.

Odgovor je. Želeni rob je 5 cm.

Peta naloga. Stanje Glede na ravno paralelepiped. Na njeni podlagi je paralelogram s stranicami 6 in 8 cm, akutni kot med katerim je 30 °. Stranski rob ima dolžino 5 cm, zato je potrebno izračunati skupno površino paralelepipeda.

Odločitev. To je primer, ko morate ločeno poznati območje vseh obrazov. Ali, natančneje, tri pare: bazo in dve strani.

Ker se paralelogram nahaja na dnu, se njegovo območje izračuna kot zmnožek strani in višine. Stran je znana, vendar višina ni. To je treba prešteti. Za to bo potrebna ostra kotna vrednost. Višina se oblikuje v paralelogramu pravokotni trikotnik. V njej je noga enaka zmnožku sinusnega akutnega kota, ki je nasproten, s hipotenuzo.

Naj bo znana stran vzporednika "a". Potem bo višina zapisana kot * sin 30º. Osnovna površina je torej * c * sin 30º.

S stranskimi robovi je vse lažje. To so pravokotniki. Zato je njihovo območje produkt ene strani na drugo. Prvi - a * s, drugi - v * s.

Preostalo je združiti vse v eno formulo in šteti:

S = 2 * (a * b * sin 30º + a * s + b * s)

Po zamenjavi vseh količin se izkaže, da je zahtevana površina 188 cm ² .

Odgovor je. S = 188 cm2.