Kaj je lomni količnik stekla? In kdaj je treba vedeti?

Pri reševanju problemov v optiki je pogosto treba poznati lomni količnik stekla, vode ali druge snovi. V različnih situacijah se lahko vključita tako absolutna kot relativna vrednost te vrednosti.

Dve vrsti lomnega indeksa

Prvič, dejstvo, da ta številka kaže: kako ta ali tisti transparentni medij spreminja smer širjenja svetlobe. In elektromagnetni val lahko pride iz vakuuma, nato pa se bo lomni količnik stekla ali druge snovi imenoval absolutni. V večini primerov je njegova vrednost v območju od 1 do 2. Samo v zelo redkih primerih je lomni količnik večji od dveh.

Če je pred subjektom gostje okolje kot vakuum, potem že govorijo o relativni vrednosti. Izračuna se kot razmerje dveh absolutnih vrednosti. Na primer, sorodnik lomni količnik steklo bo enako absolutnim vrednostim za steklo in vodo.

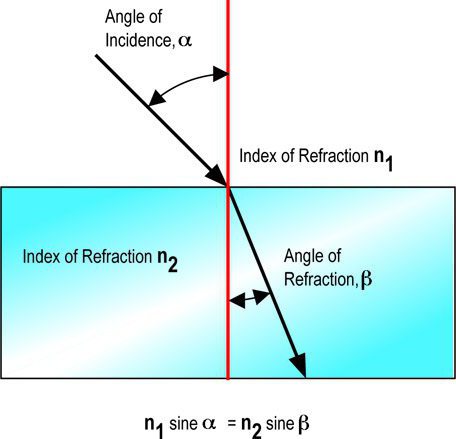
V vsakem primeru je označena z latinično črko "en" - n. Ta vrednost se dobi tako, da se med seboj delita z isto vrednostjo, zato gre preprosto za koeficient, ki nima imena.

Katero formulo lahko uporabimo za izračun indeksa loma?

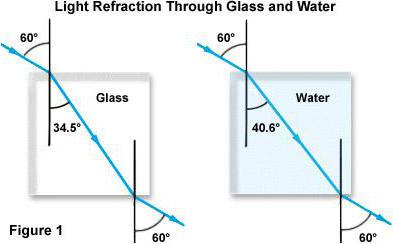
Če vzamemo kot vpada kot "alfa", in lomni kot označimo "beta", potem formula za absolutno vrednost refraktivnega indeksa izgleda takole: n = sin α / sin β. V literaturi v angleškem jeziku lahko pogosto najdete drugo oznako. Če je vpadni kot i, in lom je r.

Obstaja še ena formula, kako izračunati lomni količnik svetlobe v steklu in drugih transparentnih medijih. Povezana je s hitrostjo svetlobe v vakuumu in z njo, vendar že v obravnavani snovi.

Potem izgleda takole: n = c / νλ. Tu je c hitrost svetlobe v vakuumu, ν je njena hitrost v transparentnem mediju, in λ je valovna dolžina.

Kaj določa indeks loma?

Določena je s hitrostjo, s katero svetloba potuje v obravnavanem mediju. Zrak v zvezi s tem je zelo blizu vakuumu, zato se svetlobni valovi v njem propagirajo praktično ne odstopajo od svoje prvotne smeri. Če torej določimo lomni količnik stekla ali kakšno drugo snov, ki meji na zrak, potem je ta običajno vzeto kot vakuum.

Vsak drug medij ima svoje značilnosti. Imajo različne gostote, imajo lastno temperaturo in elastične napetosti. Vse to vpliva na rezultat loma svetlobe s snovjo.

Ne zadnjo vlogo pri spreminjanju smeri širjenja valov igrajo značilnosti svetlobe. Bela svetloba je sestavljena iz različnih barv, od rdeče do vijolične. Vsak del spektra se lomi na svoj način. Poleg tega bo vrednost indeksa za val rdečega dela spektra vedno manjša od preostalega. Na primer, lomni količnik TF-1 stekla se giblje od 1.6421 do 1.67298 oz. Od rdečega do vijoličnega dela spektra.

Primeri vrednosti za različne snovi

Tu so vrednosti absolutnih vrednosti, to je lomni količnik, ko žarek prehaja iz vakuuma (ki je enak zraku) skozi drugo snov.

Te številke bodo potrebne, če je potrebno določiti lomni količnik stekla glede na druge medije.

Katere druge vrednosti se uporabljajo pri reševanju problemov?

Popolna refleksija. Opazujemo ga, ko svetloba prehaja iz gostejšega medija v manj gosto. Tukaj, pod določenim vpadnim kotom, se refrakcija pojavi pod pravim kotom. To pomeni, da žarek drsi vzdolž meje dveh medijev.

Največji kot skupnega odboja je njegova najmanjša vrednost, pri kateri svetloba ne vstopa v manj gosto snov. Manj kot je - lom se pojavi, in še več - odsev v istem okolju, iz katerega se je svetloba premaknila.

Problem številka 1

Stanje Refrakcijski indeks stekla je 1,52. Določiti je treba mejni kot, do katerega se svetloba popolnoma odbija od ločevanja površin: steklo z zrakom, voda z zrakom, steklo z vodo.

Odločitev.

Za prikaz vode v tabeli boste morali uporabiti ta lomni količnik. To je za zrak, ki je enaka eni.

Rešitev v vseh treh primerih se zmanjša na izračune po formuli:

sin α ₀ / sin β = n ₁ / n ₂ , kjer se n ₂ nanaša na medij, iz katerega se širi svetloba, in n _1, kjer prodre.

Črka α ₀ označuje mejni kot. Vrednost kota β je 90 stopinj. To pomeni, da bo njegov sinus en.

Za prvi primer: sin α ₀ = 1 / n _steklo , potem je mejni kot enak arcsine 1 / n _stekla . 1 / 1,52 = 0,6579. Kot je 41,14º.

V drugem primeru je treba pri določanju loka nadomestiti vrednost indeksa refrakcije vode. Frakcija 1 / n _vode bo dobila vrednost 1 / 1,33 = 0, 7519. To je kot arcsine 48,75 °.

Tretji primer je opisan z razmerjem n _vode in n _stekla . Arcsine bo moral izračunati za frakcijo: 1,33 / 1,52, to je število 0,875. Vrednost omejevalnega kota najdete po njenih lokih: 61.05º.

Odgovor: 41,14 º, 48,75 º, 61,05 º.

Problem številka 2

Stanje Stekleno prizmo potopimo v posodo z vodo. Njegov lomni količnik je 1,5. Prizma temelji na pravokotni trikotnik. Večja noga je pravokotna na dno, druga pa je vzporedna z njo. Žarek svetlobe normalno pade na zgornjo površino prizme. Kakšen naj bi bil najmanjši kot med horizontalno nogo in hipotenuzo, da bi svetloba dosegla nogo, ki je pravokotna na dno posode in prišla iz prizme?

Odločitev.

Da bi žarek zapustil prizmo na opisani način, mora pasti pod skrajnim kotom na notranjem robu (tisti, ki je hipotenuza trikotnika v delu prizme). Ta mejni kot se izkaže, da je enak želenemu kotu pravokotnega trikotnika. Iz zakona loma svetlobe se izkaže, da je sinus omejevalnega kota, deljen s sinusom 90 stopinj, enak razmerju dveh lomnih količnikov: vode do stekla.

Izračuni vodijo do te vrednosti omejitvenega kota: 62 ° 30 '.

Odgovor: 62º30´.