Kaj je pospešek? Vrste pospeškov. Formule. Primer reševanja problema

Odsek fizike, ki je odgovoren za proučevanje značilnosti gibanja v prostoru teles, se imenuje kinematika. V tem članku bomo preučili, katere fizikalne veličine v kinematiki se uporabljajo za opis gibanja predmetov, in tudi razkriti, kaj je pospešek.

Fizikalne količine v kinematiki

Ko se telo giblje v prostoru, je pomembno, da vemo, kakšna razdalja potuje v določenem časovnem obdobju in po kateri poti se giblje.

Za opis prevoženih razdalj v fiziki je uporabljen koncept poti - L. V primeru gibanja po krogu se namesto poti uporablja koncept rotacijskega kota θ. Vrednost L v SI se meri v metrih (m), vrednost θ pa se meri v radianih (rad.).

Poleg poti je pomembno poznati tudi hitrost gibanja teles. Pod njim razumeti hitrost prehoda razdalj. Matematični izraz za linearno hitrost ima obliko:

v¯ = d L / dt

Za opis gibanja v krogu uporabite kotno hitrost ω, ki se izračuna na naslednji način:

ω¯ = d θ / dt

Tretja pomembna količina kinematike je pospeševanje.

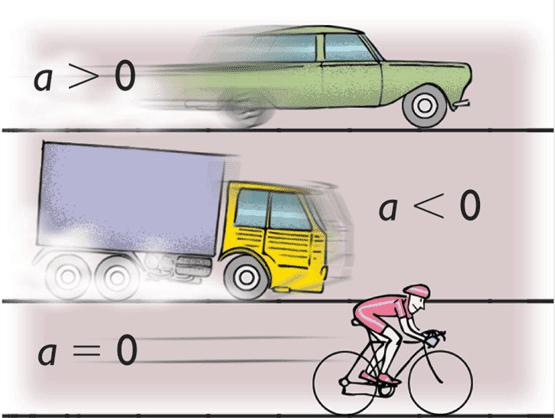
Kaj je pospešek? To je količina v fiziki, ki kaže, kako hitro se hitrost spreminja skozi čas. Matematično lahko to zapišemo kot:

a¯ = d v / dt

Če izraz za hitrost nadomestimo s formulo pospeševanja, dobimo:

a = d ² L / dt ²

Pospešek je prvi derivat hitrosti glede na čas ali drugi derivat glede na čas prehodne poti.

Tangencialni in normalni pospešek

Zgoraj je bila dana definicija pospeševanja. Imenuje se popolna. V splošnem primeru smer polnega pospeška ne sovpada s smerjo vektorja hitrosti. Slednje se dotika trajektorije gibanja na kateri koli točki.

Ker je hitrost vektorska količina, spreminjanje pomeni sposobnost spreminjanja modula in smeri. V prvem primeru pravijo, da ima telo tangencialni pospešek, v drugem primeru je normalno.

Formula za tangencialni pospešek a _t se ne razlikuje od tiste za pospeševanje polnega a. Formula ima obliko:

a _t = dv / dt

To je tangencialno ali tangencialno, kot se imenuje tudi pospešek, ki izhaja iz modula hitrosti skozi čas. Vektor a _t ¯ sovpada z vektorjem v ¯ s pospešenim gibanjem in je v nasprotju z njim s počasnim gibanjem.

Normalno pospeševanje je fizikalna količina, ki vodi do ukrivljenosti pravokotne poti gibajočih se teles. Usmerjena je po polmeru ukrivljenosti trajektorije, to je normalno glede na to. Formula za njeno opredelitev je:

a _c = v2 / r

Normalni pospešek a _{c je} odvisen od modula hitrosti v in polmera ukrivljenosti trajektorije r. Očitno je, da se v primeru gibanja vzdolž ravnega radija r lahko šteje za enako neskončnosti. Slednje pomeni, da je normalni pospešek nič za pravokotno gibanje.

Za krožno gibanje je vektor a _c ¯ usmerjen v središče vzdolž polmera. Zato se vrednost _c imenuje tudi centripetalni pospešek.

Polni pospešek

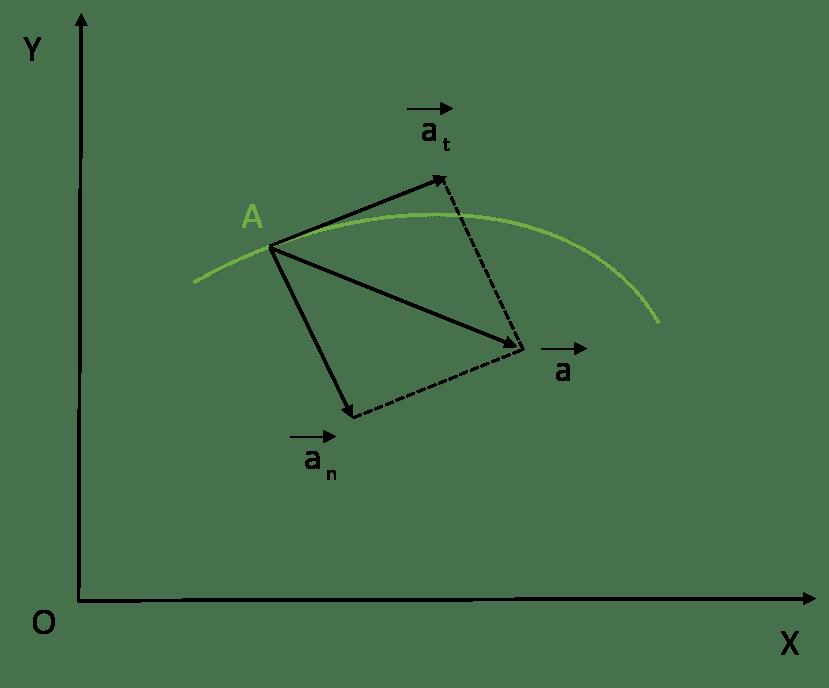
Vektor celotnega pospeška je vedno vsota tangencialnih in normalnih komponent. Ker so pravokotni drug na drugega, lahko Pitagorjev izrek uporabimo za izračun celotnega modula pospeševanja. Želena formula za popoln pospešek ima obliko:

a = √ (a _t ² + a _c ² )

Da bi ugotovili, kje je vektor a¯ usmerjen, je dovolj, da izračunamo kot med njim in katerokoli komponento. Na primer, kot φ med vektorji a in a _t je enak:

ar = arctg ( _c / a _t )

Spomnimo se, da je centripetalni pospešek neničelen le, če je krivina trajektorije drugačna od neskončnosti. V primeru pravokotnega gibanja je celotni pospešek v magnitudi in smeri enak tangencialni komponenti.

Kotni pospešek

Glede na to, da je takšno pospeševanje potrebno, se moramo zadržati na ustrezni kotni značilnosti.

Zgoraj je bil predstavljen koncept kotne hitrosti, ki se meri v radianih na sekundo (rad / s). Če najdemo derivat te hitrosti glede na čas, dobimo velikost kotnega pospeška:

α¯ = ω¯ / dt

Enostavno je pokazati, da je kotna vrednost povezana s tangencialno komponento celotnega pospeška z naslednjim razmerjem:

a _t = α × r

S konstantnim kotnim pospeškom bo tangentna komponenta a _t večja za točke, ki so bolj oddaljene od osi vrtenja.

Kotni pospešek nima nič opraviti z normalno komponento.

Reševanje problema določanja pospeška

Predpostavimo, da je telo, ki se giblje s konstanto pospeška vzdolž premice, potovalo na razdalji 100 metrov. Znano je, da je bila začetna hitrost telesa 1 m / s. Telo je prešlo označeno razdaljo v 5,5 sekundah. Kaj je pospešek gibanja?

Glede na stanje problema govorimo o enakomerno pospešenem gibanju po ravni poti. Prevožena pot se v tem primeru izračuna po formuli:

L = v ₀ × t + a × t 2/2

Iz enake vrednosti izražamo:

a = 2 × (L - v ₀ × t) / t ²

Vse vrednosti na desni strani enakosti so znane iz pogoja. Nadomestite jih in napišite odgovor: a = 6,25 m / s ² . To pomeni, da se hitrost telesa v vsakem od 5,5 sekund poveča za 6,25 m / s. Ugotovljena vrednost celotnega pospeška sovpada s tangencialno komponento.