Vektorska vrednost v fiziki: definicija, oznaka, primeri

V matematiki je vektor usmerjen segment določene dolžine. V fiziki vektorsko količino razumemo kot popolno značilnost določene fizikalne količine, ki ima modul in smer delovanja. Razmislite o osnovnih lastnostih vektorjev, kot tudi primere vektorskih fizikalnih veličin.

Skalari in vektorji

Skalari v fiziki so parametri, ki jih lahko izmerimo in predstavimo z eno samo številko. Na primer, temperatura, masa in volumen so skalari, saj se merijo s številom stopinj, kilogramov in kubičnih metrov.

V večini primerov se izkaže, da številka, ki določa skalarno vrednost, ne vsebuje izčrpnih informacij. Na primer, če upoštevamo takšno fizično lastnost kot pospešek, ne bo dovolj reči, da je 5 m / s ² , ker morate vedeti, kje je usmerjena, glede na hitrost telesa, pod določenim kotom na to hitrost ali kako drugače. Poleg pospeševanja je hitrost primer fizikalne vektorske količine. V to kategorijo spadajo tudi sila, električna poljska jakost in mnogi drugi.

Glede na definicijo vektorske količine kot segmenta, usmerjenega v prostor, ga lahko predstavimo kot množico številk (komponent vektorja), če jo gledamo v določenem koordinatnem sistemu. Najpogosteje se pri fiziki in matematiki pojavijo problemi, ki za opis vektorja zahtevajo poznavanje njegovih dveh (problemov na ravnini) ali treh komponent (problemov v prostoru).

Vektorska definicija v n-dimenzionalnem prostoru

V n-dimenzionalnem prostoru, kjer je n celo število, bo vektor enolično določen, če bodo znane njegove n komponente. Vsaka komponenta predstavlja koordinato konca vektorja vzdolž ustrezne osi koordinat, pod pogojem, da je začetek vektorja na začetku koordinatnega sistema n-dimenzionalnega prostora. Posledično lahko vektor predstavimo kot: v = {a ₁ , a ₂ , a ₃ , ..., a _n }, kjer je a ₁ skalarna vrednost prve komponente vektorja v. V skladu s tem bo v 3-dimenzionalnem prostoru vektor zapisan kot v = {a ₁ , a ₂ , a ₃ } in v dvodimenzionalnem prostoru - v = {a ₁ , a ₂ }.

Kako je navedena vrednost vektorja? Vsak vektor v 1-dimenzionalnih, dvodimenzionalnih in tridimenzionalnih prostorih lahko predstavimo kot usmerjen segment, ki leži med točkami A in B. V tem primeru je označen z AB ^→ , kjer puščica kaže, da je to vektorska vrednost. Zaporedje črk se lahko določi od začetka vektorja do njegovega konca. To pomeni, da če so koordinate točk A in B, na primer v 3-dimenzionalnem prostoru, {x ₁ , y ₁ , z ₁ } in {x ₂ , y ₂ , z ₂ }, potem bodo komponente vektorja AB ^→ enake. {x2-x ₁ , y ₂ -y ₁ , z ₂ -z ₁ }.

Grafični prikaz vektorja

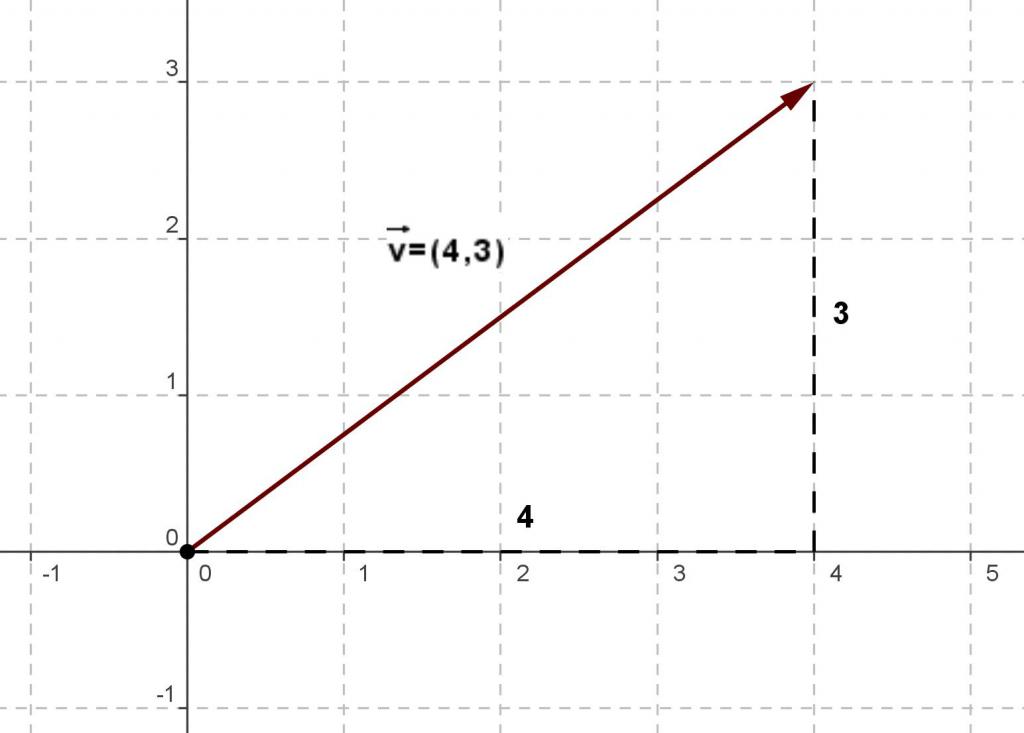
Na slikah je običajno, da je vektorska količina prikazana kot segment, na njenem koncu je puščica, ki kaže smer fizične količine, katere predstavitev je. Ta segment je običajno podpisan, na primer, v ^→ ali F ^→ , tako da je jasno, katera značilnost je mišljena.

Grafični prikaz vektorja pomaga razumeti, kje je fizična količina uporabljena in v katero smer. Poleg tega je za vektorje, ki uporabljajo njihove slike, primerno izvesti številne matematične operacije.

Matematične vektorske operacije

Vektorske vrednosti, kot tudi navadne številke, se lahko dodajo, odštejejo in pomnožijo med seboj in z drugimi številkami.

Vsota dveh vektorjev je tretji vektor, ki se dobi, če so sešteti parametri postavljeni tako, da konec prvega sovpada z začetkom drugega vektorja, nato pa poveže začetek prvega in konca drugega. Za izvedbo tega matematičnega dejanja so bile razvite tri glavne metode:

1. Metoda paralelograma, ki je sestavljena iz konstrukcije geometrijske figure na dveh vektorjih, ki prihajajo iz iste točke v prostoru. Diagonala tega paralelograma, ki sega iz skupne točke začetka vektorjev, bo njihova vsota.
2. Metoda poligona, katere bistvo je, da se začetek vsakega naslednjega vektorja postavi na konec prejšnjega, nato pa celotni vektor poveže začetek prvega in konec zadnjega.
3. Analitična metoda, ki je sestavljena iz dodatka ustreznih komponent znanih vektorjev po parih.

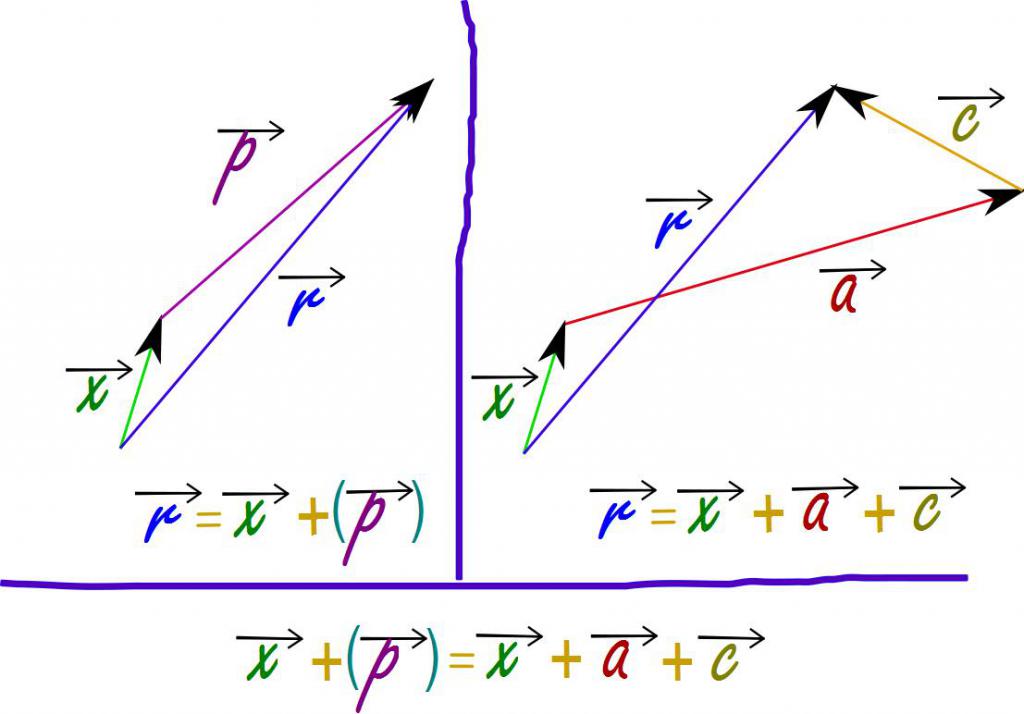
Za razliko vektorskih veličin jo lahko zamenjamo z dodajanjem prvega parametra tistemu, ki je nasproten v smeri drugega.

Množenje vektorja z določenim številom A se izvede po preprostem pravilu: to število je treba pomnožiti z vsako komponento vektorja. Rezultat je tudi vektor, katerega modul je A-krat prvotni, smer pa je bodisi enaka ali nasprotna prvotni, vse je odvisno od znaka števila A.

Vektorja ali števila nanj ni mogoče razdeliti, vendar je deljenje vektorja s številko A analogno množenju s številko 1 / A.

Skalarni in vektorski izdelek

Množenje vektorjev se lahko izvede na dva različna načina: skalar in vektor.

Skalarni produkt vektorskih veličin se imenuje takšna metoda množenja, katere rezultat je ena sama številka, to je skalar. V matrični obliki se skalarni produkt zapiše kot vrstice komponente 1. vektorja na stolpcu komponent drugega. Kot rezultat, v n-dimenzionalnem prostoru dobimo formulo: (A ^→ * B ^→ ) = a ₁ * b ₁ + a ₂ * b ₂ + ... + a _n * b _n .

V tridimenzionalnem prostoru lahko drugače definirate skalarni izdelek. V ta namen pomnožite module ustreznih vektorjev z kosinusom kota med njimi, to je (A ^→ * B ^→ ) = | A ^→ | * | B ^→ | * cos (θ _AB ). Iz te formule izhaja, da če so vektorji usmerjeni v eno smer, potem je skalarni produkt enak množenju njihovih modulov in če so vektorji pravokotni drug na drugega, potem se izkaže, da je nič. Upoštevajte, da je modul vektorja v pravokotnem koordinatnem sistemu definiran kot kvadratni koren vsote kvadratov komponent tega vektorja.

Pod vektorskim produktom razumemo množenje vektorja z vektorjem, katerega rezultat je tudi vektor. Njegova smer je pravokotna na vsak pomnožen parameter, dolžina je enaka zmnožku modulov vektorjev in sinusu kota med njimi, to je A ^→ x B ^→ = | A ^→ | * | B ^→ | * sin (θ _AB ), kjer je x označuje vektorski produkt. V matrični obliki je ta vrsta dela predstavljena kot determinanta, katere vrstice so osnovni vektorji danega koordinatnega sistema in komponente vsakega vektorja.

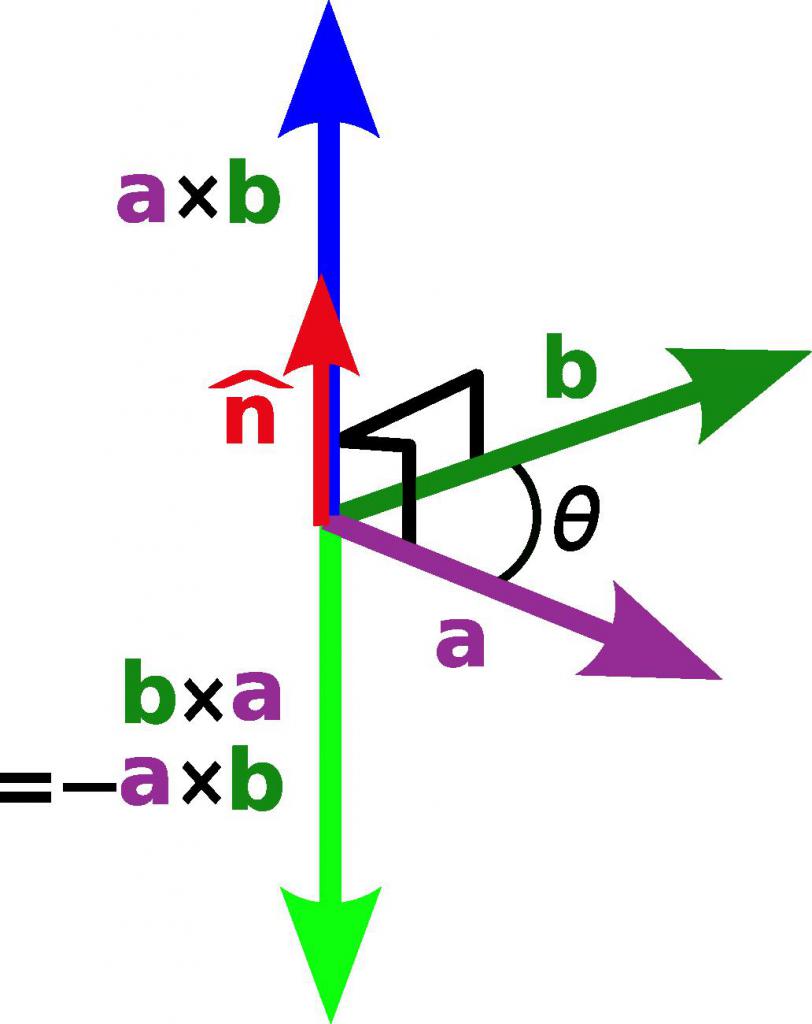
Tako skalarni kot vektorski produkti se uporabljajo v matematiki in fiziki za določanje številnih količin, na primer, območja in količine številk.

Naslednji članek podaja primere vektorskih količin v fiziki.

Hitrost in pospešek

Hitrost v fiziki je hitrost spremembe lokacije določene materialne točke. Hitrost v sistemu SI se meri v metrih na sekundo (m / s) in je označena s simbolom v ^→ . Pod pospeškom razumemo hitrost spremembe hitrosti. Pospešek se meri v metrih na kvadratni sekundi (m / s ² ) in ga običajno označuje simbol a ^→ . Vrednost 1 m / s ² pomeni, da telo vsako sekundo poveča hitrost za 1 m / s.

Hitrost in pospešek sta vektorski količini, ki sta vključeni v formule Newtonovega drugega zakona in premik telesa kot materialne točke. Hitrost je vedno usmerjena vzdolž smeri gibanja, medtem ko je pospešek lahko usmerjen samovoljno glede na premikajoče se telo.

Fizična moč

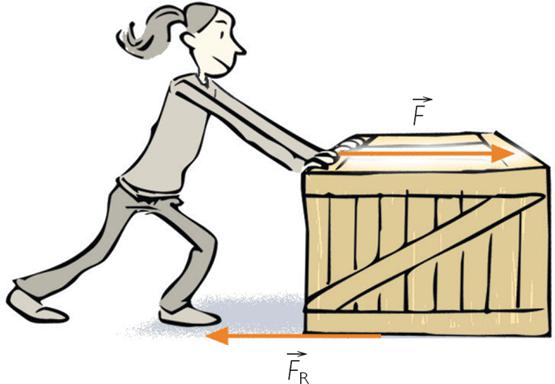
Moč je vektorska fizična količina, ki odraža intenzivnost interakcije med telesi. Označena je s simbolom F ^→ , izmerjeno v newtonih (H). Po definiciji je 1 N sila, ki lahko spreminja hitrost telesa z maso 1 kg za 1 m / s za vsako sekundo časa.

Ta fizikalna količina se pogosto uporablja v fiziki, saj je povezana z energetskimi značilnostmi procesov interakcije. Narava sile je lahko zelo različna, na primer gravitacijske sile planetov, sila, ki povzroči premikanje avtomobila, elastične sile trdnih medijev, električne sile, ki opisujejo obnašanje električnih nabojev, magnetne, jedrske sile, ki določajo stabilnost atomskih jeder, in tako naprej.

Vrednost vektorja tlaka

Druga vrednost je tesno povezana s konceptom sile - pritisk. V fiziki se razume, da pomeni normalno projekcijo sile na mesto, na katerem deluje. Ker je sila vektor, potem bo v skladu s pravilom množenja števila z vektorjem tudi tlak vektorska količina: P ^→ = F ^→ / S, kjer je S območje. Tlak se meri v paskalih (Pa), 1 Pa je parameter, pri katerem pravokotna sila 1 N deluje na površino 1 m ² . Na podlagi definicije je vektor tlaka usmerjen v isto smer kot vektor sile.

V fiziki se koncept tlaka pogosto uporablja za preučevanje pojavov v tekočinah in plinih (npr. Pascalov zakon ali enačba stanja idealnega plina). Tlak je tesno povezan s telesno temperaturo, saj kinetična energija atomov in molekul, katere predstavitev je temperatura, pojasnjuje naravo obstoja tlaka.

Električna poljska jakost

Okoli vsakega napolnjenega telesa je električno polje, katerega moč je značilna njegova intenzivnost. Ta intenzivnost je definirana kot sila, ki deluje na določeni točki električnega polja na enoti, ki se nahaja na tej točki. Intenzivnost električnega polja je označena s črko E ^→ in se meri v newtonih na obesek (H / Cl). Vektor jakosti je usmerjen vzdolž linije električnega polja v svoji smeri, če je polnitev pozitivna, in proti njej, če je naboj negativen.

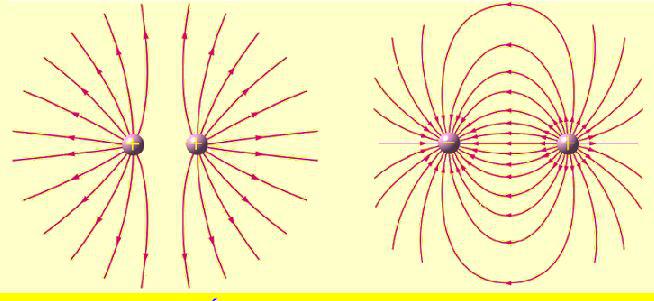
Električno polje, ki ga ustvari točkovni naboj, lahko določimo na kateri koli točki z uporabo Coulombovega zakona.

Magnetna indukcija

Magnetno polje, kot je prikazano v XIX. Stoletju, znanstveniki Maxwell in Faraday, je tesno povezano z električnim poljem. Tako spreminjajoče se električno polje generira magnetno polje in obratno. Obe vrsti polj sta torej opisani v smislu elektromagnetnih fizikalnih pojavov.

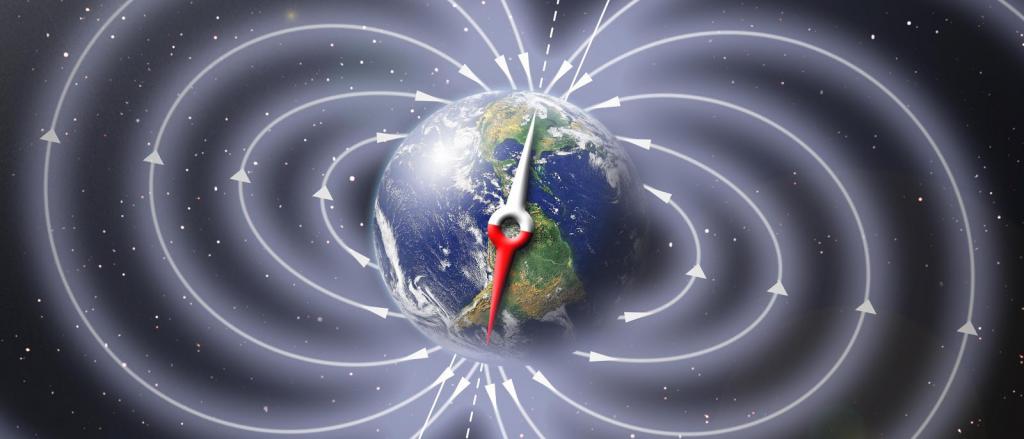
Magnetna indukcija opisuje lastnosti trdnosti magnetnega polja. Ali je magnetna indukcija skalarna ali vektorska vrednost? To lahko razumete, vedoč, da je definirana s silo F ^{→, ki} deluje na naboj q, ki pluje s hitrostjo v ^→ v magnetnem polju, po naslednji formuli: F ^→ = q * | v ^→ x B ^→ |, kjer B ^→ - magnetna indukcija. Tako lahko odgovorimo na vprašanje, ali je skalar ali vektor magnetna indukcija, lahko rečemo, da gre za vektor, ki je usmerjen od severnega magnetnega pola do južnega. Izmerjeno B ^→ v tesli (T).

Fizična kandela

Drug primer vektorske količine je kandela, ki jo v fiziko vnašamo skozi svetlobni tok, merjen v lumenih, ki poteka skozi površino, ki jo omejuje kot 1 steradian. Candela odseva svetlost svetlobe, ker kaže gostoto svetlobnega toka.