Tridimenzionalni prostor: vektorji, koordinate

Tudi iz šolskega tečaja algebre in geometrije poznamo koncept tridimenzionalnega prostora. Če razumemo, je izraz "tridimenzionalni prostor" definiran kot koordinatni sistem s tremi dimenzijami (to vedo vsi). Pravzaprav je možno opisati vsak predmet prostornine s pomočjo dolžine, širine in višine v klasičnem smislu. Vendar, kaj je, kot pravijo, kopati malo globlje.

Kaj je tridimenzionalni prostor

Kot je že postalo jasno, razumevanje tridimenzionalnega prostora in predmetov, ki so sposobni obstoja znotraj njega, določajo trije glavni koncepti. Res je, da so v primeru tocke tocno tri vrednosti in v primeru ravnih, ukrivljenih, lomljenih linij ali predmetov prostornine so lahko ustrezne koordinate vecje.

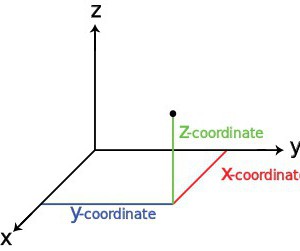
V tem primeru je vse odvisno od vrste objekta in uporabljenega koordinatnega sistema. Danes se kartezični sistem, včasih imenovan tudi pravokoten, šteje za najpogostejšega (klasičnega). O njej in nekaterih drugih vrstah bomo razpravljali kasneje.

Med drugim je treba razlikovati med abstraktnimi koncepti (če je mogoče tako reči, brezoblično), kot so točke, ravne črte ali ravnine in figure, ki imajo končne dimenzije ali enakomeren volumen. Za vsako od teh definicij obstajajo tudi lastne enačbe, ki opisujejo njihov možni položaj v tridimenzionalnem prostoru. Zdaj pa ne gre za to.

Koncept točke v tridimenzionalnem prostoru

Za začetek določimo, kaj je točka v tridimenzionalnem prostoru. Na splošno ga lahko imenujemo določeno osnovno enoto, ki definira katero koli ravno ali tridimenzionalno sliko, črto, segment, vektor, ravnino itd.

Za samo točko so značilne tri glavne koordinate. Za njih se v pravokotnem sistemu uporabljajo posebna vodila, ki se imenujejo osi X, Y in Z, pri čemer sta prvi dve osi uporabljeni za izražanje vodoravnega položaja objekta, tretja pa se nanaša na navpično določitev koordinat. Seveda, za lažje izražanje položaja objekta glede na ničelne koordinate v sistemu se predpostavljajo pozitivne in negativne vrednosti. Danes lahko najdete druge sisteme.

Vrste koordinatnih sistemov

Kot smo že omenili, je pravokotni koordinatni sistem, ki ga je ustvaril Descartes, danes glavni. Kljub temu se v nekaterih tehnikah za določanje lokacije objekta v tridimenzionalnem prostoru uporabljajo nekatere druge sorte.

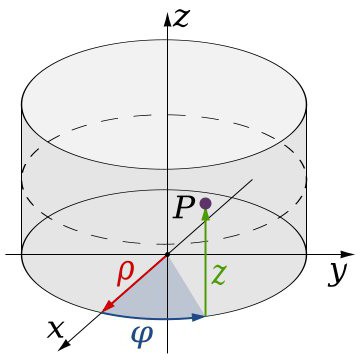
Najbolj znani so cilindrični in sferični sistemi. Razlika od klasične je v tem, da pri določanju istih treh vrednosti, ki določajo lokacijo točke v tridimenzionalnem prostoru, je ena od kotnih. Z drugimi besedami, v takih sistemih se uporablja krog, ki ustreza kotu 360 stopinj. Od tu in specifično nalogo koordinat, vključno s takimi elementi, kot so polmer, kot in generica. Koordinate v tridimenzionalnem prostoru (sistemu) tega tipa se držijo nekoliko drugačnih zakonov. Njihova naloga je v tem primeru nadzorovana s pravilom desne roke: če kombinirate palec in kazalec z osmi X in Y, bodo preostali prsti v ukrivljenem položaju označili smer osi Z.

Koncept črte v tridimenzionalnem prostoru

Zdaj pa nekaj besed o tem, kaj predstavlja ravno črto v tridimenzionalnem prostoru. Na podlagi osnovnega koncepta ravne črte je to nekakšna neskončna črta, ki poteka skozi točko ali dve, ne šteje pa več točk, ki se nahajajo v zaporedju, ki ne spreminja neposrednega prehoda črte skozi njih.

Če pogledate črto, ki poteka skozi dve točki v tridimenzionalnem prostoru, boste morali upoštevati tri koordinate obeh točk. Enako velja za segmente in vektorje. Slednji določajo osnovo tridimenzionalnega prostora in njegove dimenzije.

Definicija vektorjev in osnova tridimenzionalnega prostora

Kot se pogosto domneva, lahko v tridimenzionalnem koordinatnem sistemu obstajajo trije glavni vektorji, ki določajo osnovo. Poleg tega so lahko baze z ustreznimi neodvisnimi tremi vektorji nešteto.

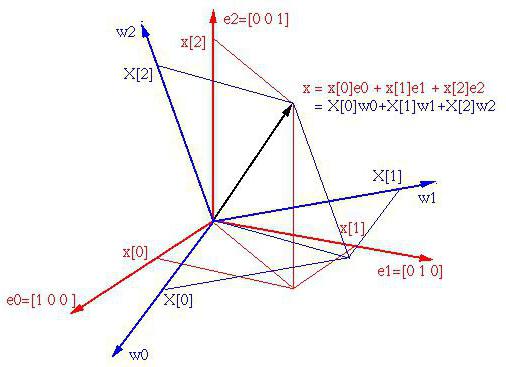
Opazite lahko, da so lahko samo trije vektorji, toda tukaj lahko definirate toliko kot trikrat vektorjev. Dimenzija prostora je določena s številom linearno neodvisnih vektorjev (v našem primeru trije). Prostor, v katerem je končno število takšnih vektorjev, se imenuje končno-dimenzionalen.

Odvisni in neodvisni vektorji

Za definicijo odvisnih in neodvisnih vektorjev velja, da so vektorji, ki so projekcije (npr. Vektorji osi X, projicirani na os Y) linearno neodvisni.

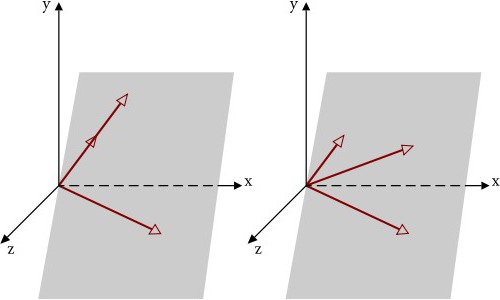
Kot je že jasno, je vsaka četrta vektor odvisna (teorija linearnih prostorov). Toda trije neodvisni vektorji v tridimenzionalnem prostoru ne smejo nujno ležati v isti ravnini. Poleg tega, če definiramo neodvisne vektorje v tridimenzionalnem prostoru, ne moremo biti, tako rekoč, eno nadaljevanje drugega. Kot je že jasno, v primeru, ko razmišljamo s tremi dimenzijami, lahko v skladu s splošno teorijo konstruiramo le tri trojice linearno neodvisnih vektorjev v določenem koordinatnem sistemu (ne glede na tip).

Ravnina v tridimenzionalnem prostoru

Če razmišljamo o konceptu ravnine, ne da bi se spuščali v matematične definicije, lahko za lažje razumevanje tega pojma tak objekt obravnavamo le kot dvodimenzionalen. Z drugimi besedami, to je neskončna zbirka točk, kjer je ena od koordinat konstanta (konstanta).

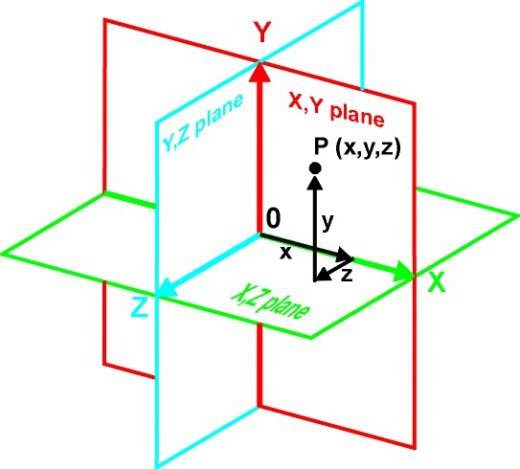
Na primer, ravnino lahko imenujemo poljubno število točk z različnimi koordinatami vzdolž osi X in Y, vendar z enakimi koordinatami vzdolž osi Z. V vsakem primeru ostane ena od tridimenzionalnih koordinat nespremenjena. Vendar je to, tako rekoč, splošen primer. V nekaterih primerih se lahko tridimenzionalni prostor križa z ravnino vzdolž vseh osi.

Ali obstaja več kot tri dimenzije

Vprašanje, koliko meritev lahko obstaja, je zelo zanimivo. Domneva se, da ne živimo v tridimenzionalnem od klasičnega vidika prostora, ampak v štirih dimenzijah. Poleg dobro znanih dolžin, širin in višin ta prostor vključuje tudi življenjsko dobo objekta, čas in prostor sta med seboj precej močno povezana. To je dokazal Einstein v svoji teoriji relativnosti, čeprav se to bolj nanaša na fiziko kot na algebre in geometrijo.

Še eno zanimivo dejstvo je, da so danes znanstveniki že dokazali obstoj vsaj dvanajstih dimenzij. Seveda, daleč od vsakogar bo mogoče razumeti, kaj so, ker se nanaša bolj na določeno abstraktno območje, ki je zunaj človeškega dojemanja sveta. Kljub temu ostaja dejstvo. Mnogi antropologi in zgodovinarji trdijo, da so naši predniki lahko imeli nekaj specifičnih čutnih organov, kot je tretje oko, ki je pomagalo zaznati večdimenzionalno resničnost in ne le tridimenzionalni prostor.

Mimogrede, danes obstaja precej mnenj o tem, da je ekstrasenzorno zaznavanje tudi ena od manifestacij percepcije večdimenzionalnega sveta in da je mogoče najti precej dokazov.

Upoštevajte, da sodobne osnovne enačbe in izreki opisujejo večdimenzionalne prostore, ki se razlikujejo od našega štiridimenzionalnega sveta, prav tako ni vedno mogoče. In znanost na tem področju se bolj nanaša na področje teorij in predpostavk kot na tisto, kar se lahko jasno čuti ali, če se tako reče, dotakne ali vidi iz prve roke. Kljub temu pa je posredni dokaz obstoja večdimenzionalnih svetov, v katerih je lahko štiri ali več dimenzij, danes nedvomno.

Zaključek

Na splošno smo na kratko pregledali osnovne pojme, povezane s tridimenzionalnim prostorom in osnovnimi definicijami. Seveda obstaja veliko posebnih primerov, povezanih z različnimi koordinatnimi sistemi. Poleg tega smo se trudili, da ne bi šli v divjino matematike, da bi razložili osnovne pojme, le da je vprašanje, ki je povezano z njimi, razumljivo vsakemu učencu (tako rekoč, razlaga je »na prstih«).

Kljub temu se zdi, da tudi iz tako preprostih interpretacij lahko sklepamo, da je matematični vidik vseh komponent vključen v osnovni šolski tečaj algebre in geometrije.