Koncept vrtilne količine, njegov zakon ohranjanja in primer reševanja problema

Rotacijsko gibanje v naravi ni manj pogosto kot linearno gibanje predmetov. Da bi to preverili, je dovolj, da se spomnimo vrtenja koles avtomobilov in koles, lopatic helikopterjev in ventilatorjev, planetov okrog svoje osi in okoli njenih zvezd. Za opis procesa krožnega gibanja predmetov se uporablja fizikalna količina, ki se imenuje "kotni moment". Razmislite v članku, kaj je to.

Momentumski moment delca in os vrtenja

Spodaj je prikazana risba, ki shematsko prikazuje, da se delci ali materialne točke mase m gibajo vzdolž krožne poti polmera ¯ s hitrostjo ν, usmerjeno tangencialno. Os vrtenja je pravokotna na ravnino slike na točki O.

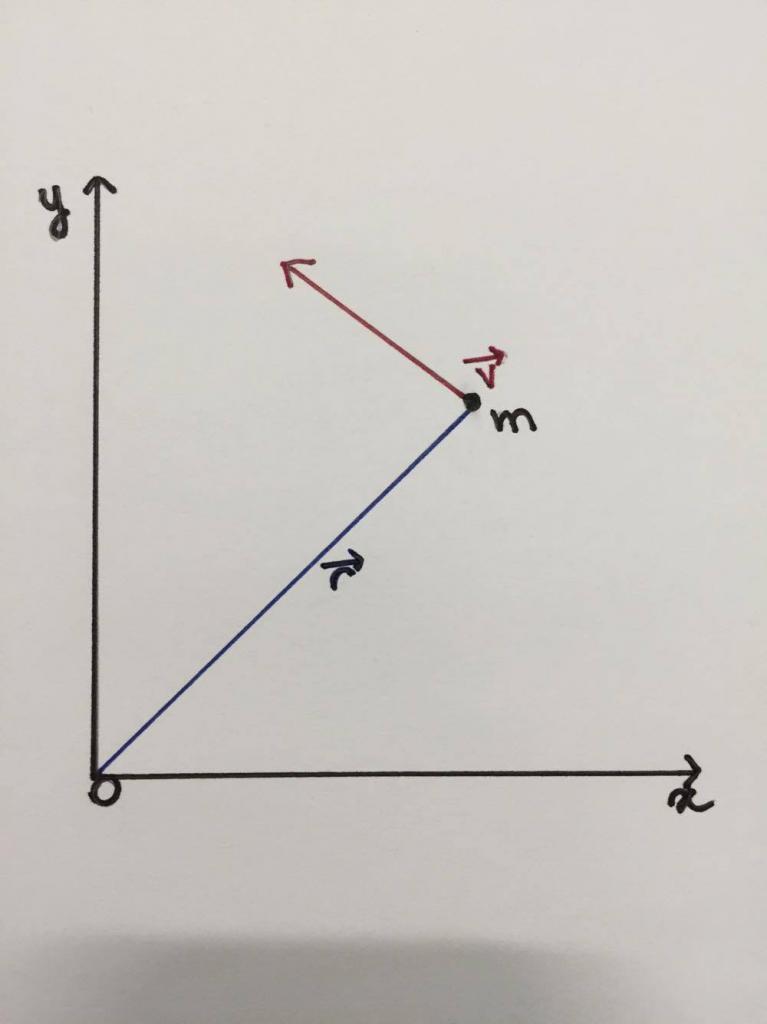
Vnesemo naslednjo fizično količino:

L¯ = r¯ * m * v¯ = r¯ * p¯.

Imenuje se kot kotni moment ali kotni moment. Kot lahko vidite, je to vektorska količina. Njegovo smer lahko določimo s pravilom desne roke: usmerimo 4 prste tako, da se premikajo vzdolž vektorja r¯, pridejo na konec vektorja p ¯ (ali v¯), nato palec pokaže smer L¯. V tem primeru je L¯ usmerjen na čitalnik pravokotno na ravnino za risanje.

Ker je hitrost delcev (impulz) na sliki usmerjena pod pravim kotom na vektor ¯, lahko enačbo prepišemo v skalarni obliki:

L = r * m * v = r * str.

Kotna hitrost in vztrajnostni moment

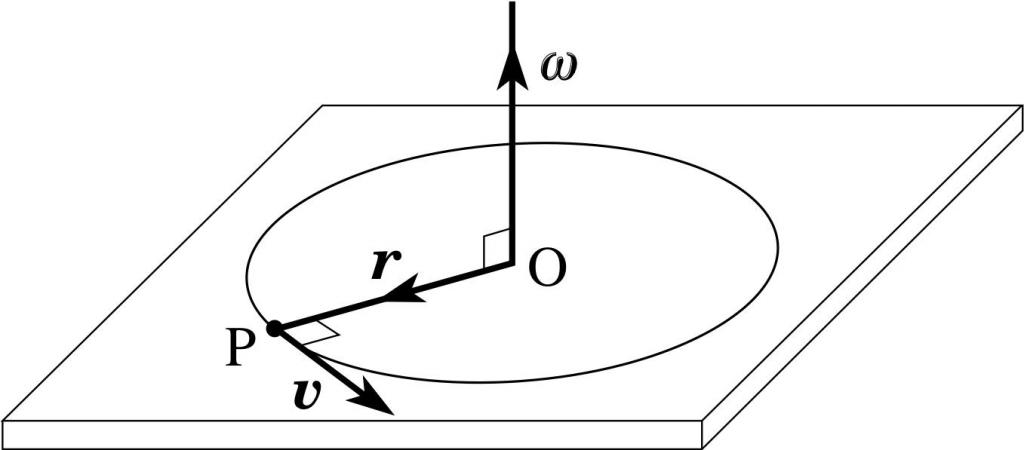
Hitrost delca iz prejšnjega primera lahko zapišemo skozi kotno hitrost ω. V ta namen uporabimo njegovo povezavo z linearno hitrostjo:

ω = v / r => v = ω * r.

Če nadomestimo zadnjo enačbo v skalarno enačbo za L, dobimo:

L = r ² * m * ω = I * ω, kjer je I = r ² * m.

Tu je I trenutek vztrajnosti delca. Izraz, ki izhaja iz tega, se pogosto uporablja za reševanje praktičnih problemov, od katerih bo ena obravnavana spodaj.

Zakon ohranjanja rotacijskega gibanja

Gibanje v krogu, kot tudi linearno gibanje predmetov v prostoru, je označeno z zakoni o ohranjanju. Eden od njih je ohranjanje kotne količine. Dobimo ta zakon.

Enačba obravnavanega tipa gibanja ima naslednjo obliko:

dL / dt = M.

Kjer dL / dt označuje spremembo momenta gibanja telesa skozi čas, ko na njega vpliva določen trenutek M, ki ga ustvarjajo zunanje (ne notranje) sile. Če je ta trenutek sile enak nič, potem leva stran izraza izgine, kar pomeni L = const. V tem primeru lahko zapišemo naslednjo enakost:

L = konst = I ₁ * ω ₁ = I ₂ * ω ₂ .

Kaj pomeni ta zapis? Pravi, da če je neko telo zavrtelo s hitrostjo ω ₁ in je imelo vztrajnostni moment I ₁ , se je zaradi nekaterih notranjih (ne zunanjih) sil trenutek vztrajnosti spremenil in postal enak I ₂ , potem bo nova hitrost vrtenja ω ₂ sorazmerna povezane s to spremembo.

Zabeleženo razmerje se po analogiji z ustreznim zakonom za linearne količine (ohranjanje momenta) imenuje zakon ohranjenosti momentne točke točke (telesa), ker je v trenutku mase vztrajnostni moment I, kot pa masa je kotna vrednost ω.

Uporaba zakona L = const

Razmerje, obravnavano v prejšnjem odstavku, je vidno v akciji, ko nastopajo drsalci ali balerine. Izvajajo zapletene akrobacije, vrtijo svoja telesa, razpršijo roke in noge in nato pritisnejo okončine proti telesu. Zadnji ukrep vodi do zmanjšanja vrednosti I in s tem do povečanja hitrosti vrtenja, kar ustvarja dokaj spektakularen učinek.

Drug primer uporabe nespremenljivosti kotne količine sistema je izvedba rotacije umetnega satelita v vesolju. V ta namen vstavite poseben vztrajnik. Ker se skupni moment ne sme spreminjati zaradi delovanja notranjih sil, se satelit začne vrteti v nasprotni smeri. Takoj, ko se obrne na želeni kot okrog svoje osi, se vztrajnik ustavi s pomočjo električnega motorja, satelitsko telo pa ustavi tudi njegovo vrtenje.

Izračunajte trenutek vztrajnosti

Ker je vrednost I prisotna v zakonu ohranjanja krožnega gibanja, bi morali povedati nekaj besed o tem. Značilna je vztrajnost sistema, to je, kako ga je "težko" ali "enostavno" sprostiti. Na primer, vztrajnik avtomobila ima veliko maso in razmeroma velik radij, zato je njegov vztrajnostni moment pomemben. Nasprotno, kolesno kolo je izdelano iz aluminijastega svetlobnega platišča, zato bom zanj relativno majhna.

Za izračun te fizikalne lastnosti uporabite formulo:

I = ( _m (r ² * dm).

Od tod je razvidno, da je trenutek vztrajnosti značilnost sistema, v katerega vstopa telo revolucije, in ne telo samega. To dejstvo me razlikuje od linearne inercije, ki je odvisna samo od lastnosti telesa (njegove mase).

Naloga z vrtljivo palico

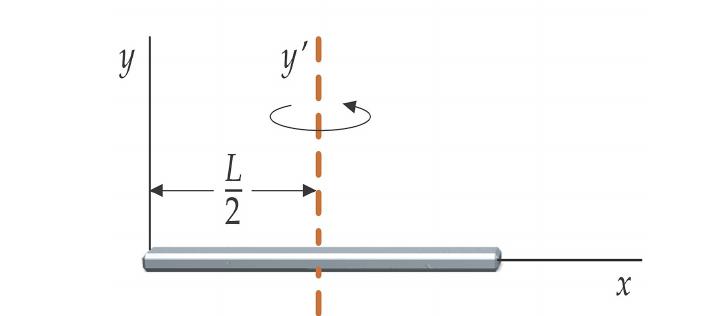
Rešili bomo zanimiv problem: obstaja trdna palica, ki se vrti okoli osi, ki se nahaja na njenem koncu. Če se ta os gladko premakne v središče mase palice, kako se bo spremenila njena hitrost vrtenja?

To je klasična naloga, da uporabimo zakon ohranjanja vrtilne količine. Težava je v izračunu spremembe vztrajnosti. Da bi to naredili, lahko uporabimo zgornjo formulo z integralom, vendar bo lažje pogledati potrebne vrednosti I v referenčni literaturi.

Na začetku je vrtilna os potekala skozi konec palice. Za ta sistem je vztrajnostni moment enak:

I ₁ = m * L 2/3, kjer je L dolžina palice, m je njena masa.

Ko je bila os premaknjena v središče mase objekta, se je njegov moment vztrajnosti spremenil, postal je enak:

I ₂ = m * L 2/12.

Uporabite zakon o ohranitvi za L, dobimo:

m * L 2/3 * ω ₁ = m * L 2/12 * ω ₂ => ω ₂ / ω ₁ = m * L 2/3 / (m * L 2/12) = 4.

Prejeli smo odgovor na težavo: palica se bo vrtela 4-krat hitreje kot na začetku.