Simetrala trikotnika - kaj je to?

Geometrija je ena najbolj zapletenih in zapletenih znanosti. V njem se zdi, da je na prvi pogled očitno, da je to zelo redko. Bisektorji, višine, mediane, projekcije, tangente so veliko število res težkih izrazov, s katerimi se lahko zelo zmedejo.

Pravzaprav lahko s pravilno željo razumete teorijo poljubne kompleksnosti. Ko pride do simetrala, mediana in višina, morate razumeti, da niso značilni za trikotnike. Na prvi pogled so to preproste linije, vendar vsaka od njih ima svoje lastnosti in funkcije, katerih poznavanje močno poenostavlja rešitev geometrijskih problemov. Torej, kaj je simetrala trikotnika?

Opredelitev

Izraz "simetrala" izhaja iz kombinacije latinskih besed "dva" in "cut", "cut", ki posredno kaže njene lastnosti. Običajno, ko se otroci seznanijo s tem žarkom, so zaprošeni, da si zapomnijo kratek stavek: "Simetrala je podgana, ki teče po vogalih in prepolovi kot." Seveda takšna razlaga ni primerna za starejše študente, poleg tega pa se običajno ne sprašujejo o premogu, ampak o geometrijska oblika. Simetrala trikotnika je torej žarek, ki povezuje vrh trikotnika z nasprotno stranjo, pri čemer razdeli kot na dva enaka dela. Točka nasprotne strani, na katero pride simetrala, za poljuben trikotnik se izbere naključno.

Osnovne funkcije in lastnosti

Glavne lastnosti tega žarka malo. Prvič, ker simetrala trikotnika deli kot na polovico, bo vsaka točka, ki leži na njem, na enaki razdalji od strani, ki tvorijo vrh. Drugič, v vsakem trikotniku lahko narišemo tri bisektrike, glede na število razpoložljivih kotov (zato jih bo že v štirih štirikotnikih, in tako naprej). Točka, v kateri se vsi trije žarki sekajo, je središče kroga, vpisanega v trikotnik.

Lastnosti so zapletene

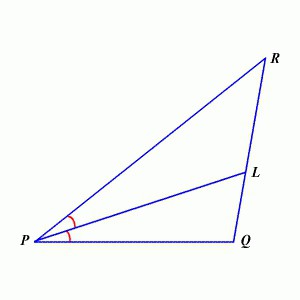
Malo zapletamo teorijo. Še ena zanimiva lastnost: simetrala kota trikotnika deli nasprotno stran na segmente, katerih razmerje je enako razmerju stranic, ki tvorijo vrh. Na prvi pogled je to težko, v resnici pa je vse preprosto: v predlagani sliki je RL: LQ = PR: PK. Mimogrede, ta lastnost se je imenovala Teorem o Bisektriki in se prvič pojavila v delih starega grškega matematika Evklida. Spomnili so jo v enem od ruskih učbenikov šele v prvi četrtini 17. stoletja.

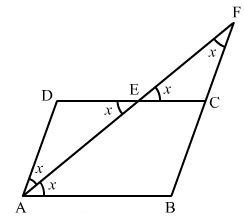
Malo težje. V štirikotniku simetrala odseka enakokračni trikotnik. Na tej sliki so prikazani vsi enaki koti sredinskega AF.

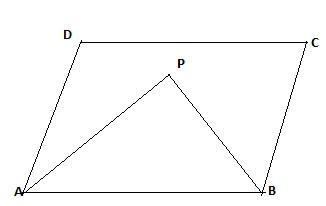
Poleg tega so v štirikotnikih in trapezih bisektorji enostranskih kotov med seboj pravokotni. Na risbi je kot APB 90 stopinj.

V enakokraki trikotnik

Enakokraki enakokraki trikotnik je veliko bolj koristen žarek. To je hkrati ne le delilo vogala na pol, ampak tudi mediana in višina.

Mediana je segment, ki izhaja iz določenega kota in pade na sredino nasprotne strani in ga deli na enake dele. Višina je pravokotnica, ki je padla iz vozlišča na nasprotno stran, s katero se lahko vsaka naloga skrči na preprost in primitiven Pitagorjev izrek. V tem primeru je simetrala trikotnika enaka korenu razlike med kvadratom hipotenuze in drugim krakom. Mimogrede, prav ta lastnost se najpogosteje najde v geometrijskih težavah.

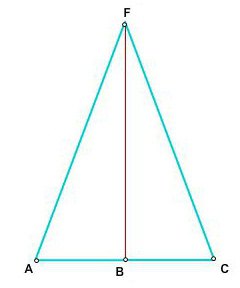
Če želite popraviti: v tem trikotniku je simetrala FB mediana (AB = BC) in višina (koti FBC in FBA sta 90 stopinj).

Na splošno

Torej, kaj morate zapomniti? Simbol trikotnika je žarek, ki razdeli svoj vrh na pol. Na presečišču treh žarkov je središče kroga, vpisanega v ta trikotnik (edina pomanjkljivost te lastnosti je, da nima praktične vrednosti in služi le za pravilno izvedbo risbe). Prav tako deli nasprotno stran na segmente, katerih razmerje je enako razmerju stranic, med katerimi je ta žarek minil. V štirikotniku so lastnosti nekoliko bolj zapletene, vendar se priznavajo, da se praktično ne pojavljajo v nalogah na ravni šole, zato jih program običajno ne vpliva.

Simetrala enakokrakega trikotnika je končna sanja vsakega študenta. Hkrati je mediana (to pomeni, da razdeli nasprotno stran na polovico) in višino (pravokotno na to stran). Reševanje problemov s takšno simetralo se zmanjša na Pitagorov izrek.

Poznavanje osnovnih funkcij simetrale in njenih osnovnih lastnosti je potrebno za reševanje geometrijskih problemov tako srednje kot visoke stopnje kompleksnosti. Dejstvo je, da se ta žarek nahaja le v planimetriji, zato je nemogoče reči, da bo pomnjenje informacij o tem omogočilo spopadanje z vsemi vrstami nalog.