Kako najti hipotenuzo: 4 načinov za iskanje odgovora

Po študiju teme desni trikotniki študenti pogosto zavržejo vse informacije o njih. Vključno s tem, kako najti hipotenuzo, da ne omenjam, kaj je to.

In zaman. Ker se kasneje izkaže, da je diagonala pravokotnika ta hipotenuza, jo je treba najti. Or premer kroga sovpada z največjo stranjo trikotnika, katerega vogal je ravna. In da bi jo našli brez tega znanja, je nemogoče.

Obstaja več možnosti za iskanje hipotenuze trikotnika. Izbira metode je odvisna od začetnega niza podatkov v izpisu vrednosti problema.

Metoda št. 1: oba sta navedena

To je najbolj znamenita metoda, ker uporablja Pitagorov izrek. Samo včasih študenti pozabijo, da je ta formula kvadrat hipotenuze. Torej, da bi našli samo stran, boste morali izvleči kvadratni koren. Zato bo formula za hipotenuzo, ki je običajno označena s črko "c", videti takole:

c = √ ( ² + v ² ) , kjer ^sta črki pravokotnega trikotnika napisani s črkama „a“ in „b“.

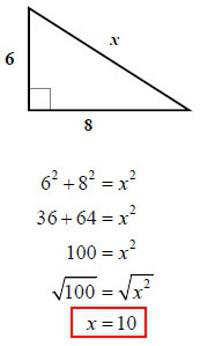
Način št. 2: Znan na nogo in kot, ki je ob njem

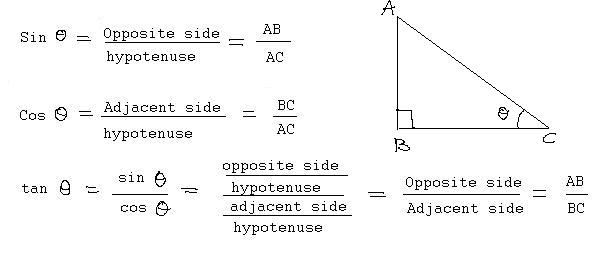
Če želite izvedeti, kako najti hipotenuzo, se boste morali spomniti trigonometričnih funkcij. In sicer kosinus. Za udobje predpostavimo, da sta podani noga "a" in kot α, ki ju nalezeta.

Zdaj se moramo spomniti, da je kosinus kota pravokotnega trikotnika enak razmerju obeh strani. Števec bo vrednost noge in imenovalec - hipotenuza. Iz tega sledi, da se slednje lahko šteje po formuli:

c = a / cos α .

Metoda št. 3: glede na nogo in kot, ki leži nasproti njega

Da ne bi dobili zmede v formulah, vpišemo zapis za ta kot - β in stran zapustimo kot pred “a”. V tem primeru je potrebna druga trigonometrična funkcija, sinus.

Kot v prejšnjem primeru je sinus enak razmerju noge do hipotenuze. Formula za to metodo je naslednja:

c = a / sin β .

Da se ne bi zapletli v trigonometrične funkcije, se lahko spomnite preprostega mnemoničnega pravila: če se težava ukvarja z nasprotnim kotom, potem morate uporabiti s in nus, če gre za pr in leži, potem o sinusu. Pozornost je treba nameniti prvim samoglasnikom ključnih besed. Oblikujejo pare o-in ali -o .

Metoda št. 4: vzdolž oboda krožnice

Zdaj, da se naučimo, kako najti hipotenuzo, moramo opozoriti na lastnost kroga, ki je opisan okoli pravokotnega trikotnika. Besedilo se glasi: t Središče kroga sovpada s sredino hipotenuze. Drugače rečeno, največja stran pravokotnega trikotnika je diagonala kroga. To je dvojni polmer. Formula za to nalogo bo izgledala takole:

c = 2 * r , kjer je r znan polmer.

To so vsi možni načini iskanja hipotenuze pravega trikotnika. Za uporabo v vsaki posamezni nalogi potrebujete metodo, ki je primernejša za podatkovni niz.

Primer problema številka 1

Pogoj: v pravokotnem trikotniku so mediane potegnjene na obe nogi. Dolžina tistega, ki se drži do večje strani, je .52. Druga srednja vrednost je dolgo 73. Potreben je izračun hipotenuze.

Odločitev.

Ker so mediane narisane v trikotniku, delijo noge na dva enaka segmenta. Za udobje, razmišljanje in ugotovitev, kako najti hipotenuzo, morate vnesti nekaj simbolov. Obe polovici večjega katetusa naj bodo označeni s črko »x«, druga pa z »y«.

Zdaj moramo razmisliti o dveh pravih trikotnikih, od katerih sta hipotenuzi znana mediana. Za njih morate pisati dvakrat Formula za pitagorejski izrek :

(2y) ² + x ² = ()52) ²

in

(y) ² + (2x) ² = ()73) ² .

Ti dve enačbi tvorita sistem z dvema neznankama. Ko jih rešimo, bomo lahko našli noge prvotnega trikotnika in po njihovem hipotenuza.

Najprej morate graditi vse do druge stopnje. Izkazalo se je:

4y ² + x ² = 52

in

pri ² + 4x ² = 73.

Iz druge enačbe je razvidno, da je ² = 73 - 4x ² . Ta izraz je treba nadomestiti s prvim in izračunati "x":

4 (73 - 4x ² ) + x ² = 52.

Po konverziji:

292 - 16 x ² + x ² = 52 ali 15 x ² = 240.

Iz zadnjega izraza x = =16 = 4.

Zdaj lahko izračunate "y":

y ² = 73 - 4 (4) ² = 73 - 64 = 9.

y = 3.

Glede na stanje se izkaže, da so noge prvotnega trikotnika 6 in 8. Zato lahko uporabite formulo iz prve metode in poiščete hipotenuzo:

√ (6 ² + 8 ² ) = √ (36 + 64) = =100 = 10.

Odgovor : hipotenuza je 10.

Primer naloge 2

Pogoj: izračunajte diagonalno črto v pravokotniku z manjšo stranjo, ki je enaka 41. Če je znano, da ta kot deli s tistimi, ki se nanašajo na 2 do 1.

Odločitev.

Pri tej nalogi je diagonala pravokotnika največja stran v trikotniku s kotom 90 °. Zato se vse zdi, kako najti hipotenuzo.

Problem je v kotih. To pomeni, da boste morali uporabiti eno od formul, v katerih so trigonometrične funkcije. In najprej morate določiti vrednost enega od ostrih vogalov.

Naj bo manjši od kotov, omenjenih v pogoju, α. Potem bo desni kot, ki ga delimo z diagonalo, enak 3α. Matematična oznaka za to je:

90º = 3 α.

Iz te enačbe preprosto določimo α. To bo enako 30 °. In leži nasproti manjše strani pravokotnika. Zato boste potrebovali formulo, opisano v metodi številka 3.

Hipotenuza je enaka razmerju med nogo in sinusom nasprotnega kota, to je:

41 / sin 30º = 41 / (0.5) = 82.

Odgovor: hipotenuza je 82.