Kako najti višino trapeza: formula za vse priložnosti
Na preprosto vprašanje »Kako najti višino trapeza?« Obstaja več odgovorov, vse zato, ker je mogoče dati različne začetne vrednosti. Zato se formule razlikujejo.
Te formule je mogoče zapomniti, vendar jih je mogoče enostavno izpeljati. Potrebno je le uporabiti predhodno preučene teoreme.
Sprejeta v formulah
V vseh spodaj navedenih matematičnih zapisih so točne črke pravilne.
| poljuben trapez | enakokraki trapez | ime |
| a | a | dno |
| v | v | na vrhu |
| c, d | z | strani |
| n | n | višino |
| m | m | srednja črta |
| d 1 d 2 | d 1 | diagonale |
| s | s | kvadrat |
| α, β | α | spodnji vogali spodaj |
| γ, δ | γ, δ | koti na preseku diagonal |
V izvornih podatkih: vse strani
Da bi našli višino trapeza v splošnem primeru, morate uporabiti naslednjo formulo:
n = √ (c 2 - (((a - c) 2 + c 2 - d 2 ) / (2 (a - c)) 2 ). Številka 1.
Ni najkrajša, vendar je v nalogah precej redka. Običajno lahko uporabite druge podatke.
Formula, ki vam pove, kako najti višino enakokrakega trapeza v isti situaciji, je veliko krajša:
n = √ (c 2 - (a - c) 2/4). Številka 2
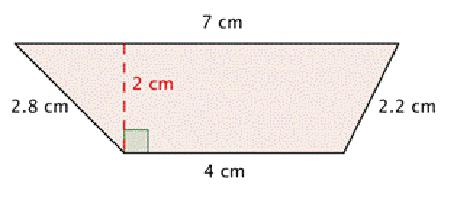
V problemu so podane stranice in koti na spodnji podlagi
Predvideva se, da je kot a v bližini strani z oznako "c" oziroma kota β na strani d. Potem bo formula za iskanje višine trapeza na splošno:
n = c * sin α = d * sin β. Številka 3
Če je številka enakokračna, lahko uporabite to možnost:
n = c * sin α = ((a - c) / 2) * tg α. Številka 4
Znano: diagonale in koti med njimi
Običajno se tem podatkom pridružijo še znane vrednosti. Na primer, osnovna ali srednja linija. Če so podani razlogi, potem je odgovor na vprašanje, kako najti višino trapeza, koristen v naslednji formuli:
n = (d 1 * d 2 * sin γ) / (a + b) ali n = (d 1 * d 2 * sin δ) / (a + b). Številka 5.
To je za celoten videz slike. Če je podan izoscen, se zapis pretvori na naslednji način:
n = (d 1 2 * sin γ) / (a + b) ali n = (d 1 2 * sin δ) / (a + b). Številka 6.
Ko se problem ukvarja s središčnico trapeza, postanejo formule za iskanje njegove višine naslednje:
n = (d 1 * d 2 * sin γ) / 2m ali n = (d 1 * d 2 * sin δ) / 2m. Soba 5a.
n = (d 1 2 * sin γ) / 2m ali n = (d 1 2 * sin δ) / 2m. Številka 6a.
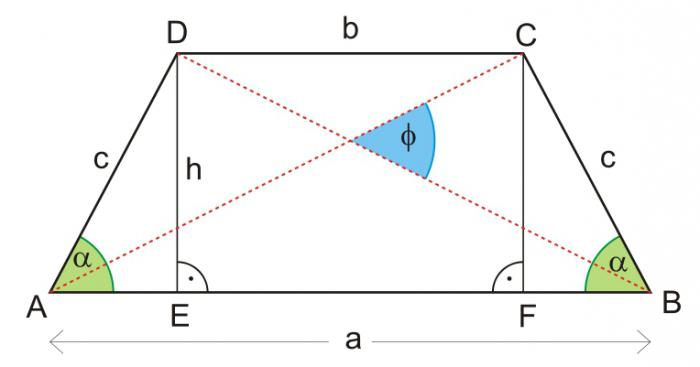
Med znanimi vrednostmi: območje z bazami ali srednja črta
To so morda najkrajše in najpreprostejše formule za iskanje višine trapeza. Za poljubno obliko bo:
n = 2S / (a + c). Številka 7.
Enako je, vendar z dobro znano srednjo črto:
n = s / m. Soba 7a.
Nenavadno je, toda za enakokračni trapez, bodo formule izgledale enako.
Naloge
№1. O definiciji kotov na dnu trapeza.
Stanje Podan je enakokračni trapez, katerega stran je 5 cm, njegove osnove so 6 in 12 cm, potrebno pa je najti sinus akutnega kota.
Odločitev. Za udobje morate vnesti zapis. Naj bo spodnja leva tocka A, vse ostalo v smeri urinega kazalca: B, C, D. Tako bo spodnja baza označena z HELL, zgornja baza bo BC.
Višine je treba narisati iz tock B in C. Tocke, ki kažejo konce višin, bodo oznaćene s H 1 in H 2 . Ker so na sliki BCH 1 H 2 vsi koti ravni, je pravokotnik. To pomeni, da je segment H1H2 6 cm.
Zdaj moramo razmisliti o dveh trikotnikih. So enake, ker so pravokotne z identično hipotenuzo in navpičnimi nogami. Iz tega sledi, da so njihove manjše noge enake. Zato jih lahko opredelimo kot količnik razlike. Slednje se dobi z odštevanjem od spodnje osnove zgornjega. Razdeli jo bomo z 2. To pomeni, da moramo 12 - 6 deliti z 2. AN 1 = H 2 D = 3 (cm).
Zdaj iz Pitagorejevega izreka morate najti višino trapeza. Potrebno je najti sinus kota. BH 1 = √ (5 2 - 3 2 ) = 4 (cm).
Z znanjem o tem, kako je sinus akutnega kota v pravokotnem trikotniku, lahko zapišemo naslednji izraz: sin α = BH 1 / AB = 0.8.
Odgovor je. Želeni sinus je 0,8.
№2. Najti višino trapeza z znamenito tangento.
Stanje Za enakokračni trapez, morate izračunati višino. Znano je, da so njene osnove 15 in 28 cm Dan tangente akutnega kota: 11/13.
Odločitev. Oznaka tock je enaka kot pri prejšnji nalogi. Ponovno morate imeti dve višini od zgornjih vogalov. Po analogiji z rešitvijo prvega problema moramo najti AH 1 = H 2 D, ki so definirani kot razlika 28 in 15, deljena z dve. Po izračunih se izkaže: 6,5 cm.
Ker je tangens razmerje med dvema nogama, lahko zapišemo naslednjo enakost: tg α = AH 1 / BH 1 . Poleg tega je to razmerje 11/13 (po pogojih). Ker je AN 1 znan, je mogoče izračunati višino: VN 1 = (11 * 6.5) / 13. Enostavni izračuni dajejo rezultat 5,5 cm.
Odgovor je. Potrebna višina je 5,5 cm.
№3. Za izračun višine znanih diagonal.
Stanje Za trapezo je znano, da so njegove diagonale 13 in 3 cm, potrebno pa je poznati njegovo višino, če je vsota baz 14 cm.
Odločitev. Naj bo oznaka enaka kot prej. Recimo, da je zvočnik manjša diagonala. Iz vozlišča C morate imeti želeno višino in jo označiti s CH.
Zdaj morate izvesti dodatno gradnjo. Iz kota C morate narisati ravno črto vzporedno z večjo diagonalo in najti točko njenega presečišča z nadaljevanjem strani krvnega tlaka. To bo D 1 . Izkazalo se je, da je nov trapez, znotraj katerega je narisan trikotnik ASD 1 . To je potrebno tudi za nadaljnjo rešitev problema.
Želena višina bo tudi v trikotniku. Zato lahko uporabite formule, preučene v drugi temi. Višina trikotnika je opredeljena kot zmnožek števila 2 in območje, deljeno s stranjo, na katero je narisana. In stran je enaka vsoti osnov prvotnega trapeza. To temelji na pravilu, da je bila izvedena dodatna gradnja.
V obravnavanem trikotniku so znane vse strani. Za udobje vpišemo zapis x = 3 cm, y = 13 cm, z = 14 cm.
Zdaj lahko preštejemo območje z uporabo teorema Gerone. Pol-perimeter bo p = (x + y + z) / 2 = (3 + 13 + 14) / 2 = 15 (cm). Potem bo formula za območje po zamenjavi vrednosti videti takole: S = √ (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 6 × 10 (cm 2 ).
Sedaj morate prešteti višino: n = (2 * 6) 10) / 14 = 6 /10 / 7 (cm).
Odgovor je. Višina je 6√10 / 7 cm.
№4. Za iskanje višin na straneh.
Stanje Podan je trapez, katerega tri strani so 10 cm, četrti pa 24 cm.
Odločitev. Ker je številka enakokračna, boste potrebovali formulo številka 2. V njej boste morali le nadomestiti vse vrednosti in šteti. Izgledalo bo tako:
n = √ (10 2 - (10 - 24) 2/4) = (51 (cm).
Odgovor je. n = 51 cm