Kako najti prave številke?

Številke so različne: naravne, naravne, racionalne, cele in delne, pozitivne in negativne, kompleksne in preproste, nenavadne in parne, realne itd. Iz tega članka se lahko naučite, kaj so preproste številke.

Katere številke imenujemo angleška beseda "simpl"?

Zelo pogosto, študenti na eni od najbolj enostavnih na prvi pogled vprašanja matematike, o tem, kaj je glavna številka, ne vedo, kako odgovoriti. Pogosto zamenjujejo preproste številke z naravnimi številkami (tj. Številkami, ki jih ljudje uporabljajo pri štetju postavk, v nekaterih virih pa od nič, v drugih pa od enega). Ampak to sta popolnoma dve različni stvari. Prvotne številke so naravne, to so cela števila in pozitivna števila, ki so večja od ene in imajo samo 2 naravni delilnika. V tem primeru je eden od teh deliteljev dano število, drugo pa eno. Tri so na primer praštevilo, saj ni deljivo z nobeno drugo številko, ki ni sama in ena.

Sestavljene številke

Nasprotje primes je sestavljeno. Prav tako so naravni, tudi več kot eni, vendar nimajo dveh, ampak večjega števila delilnikov. Na primer, številke 4, 6, 8, 9 itd. So naravne, sestavljene, vendar ne prave številke. Kot lahko vidite, so to večinoma parne številke, vendar ne vse. Toda “dva” - celo število in “prva številka” v nizu osnovnih števil.

Zaporedje

Če želimo zgraditi niz osnovnih števil, je treba izbrati iz vseh naravnih števil, pri čemer je treba upoštevati njihovo definicijo, to pomeni, da morate ravnati po nasprotnem. Treba je razmisliti o vsakem od pozitivnih celih števil, da ugotovimo, ali ima več kot dva delilnika. Poskusimo zgraditi niz (zaporedje), ki sestavljajo prave številke. Seznam se začne z dvema, naslednja je tri, ker je razdeljena samo na sebe in na enote. Razmislite o štirici. Ali imajo delilce razen štiri in ena? Da, to število je 2. Torej, štiri niso prave številke. Pet je prav tako preprosto (ni deljivo z nobeno drugo številko razen 1 in 5), vendar je šest deljivo. In na splošno, če sledite vsem parnim številkam, lahko vidite, da razen za »dva« nobeden od njih ni preprost. Od tu zaključujemo, da celo številke, razen dveh, niso enostavne. Še eno odkritje: vse številke, ki so deljive v tri, razen same triade, pa naj bo parno ali čudno, prav tako niso enostavne (6, 9, 12, 15, 18, 21, 24, 27 itd.). Enako velja za številke, ki so razdeljene na pet in sedem. Prav tako niso vse preproste. Povzemimo. Torej, vse številke lihih števil razen za enega in devet, in od parnih - samo "dva". Na ducate (10, 20, ... 40 itd.) Ni preprosto. Dvoštevilčne, trimestne in tako preproste številke lahko določimo na podlagi zgoraj opisanih načel: če nimajo drugih deliteljev, ki niso sami in tisti.

Teorije o lastnostih prostih števil

Obstaja znanost, ki proučuje lastnosti celih števil, vključno s številkami. To je veja matematike, ki se imenuje najvišja. Poleg lastnosti celih števil se ukvarja tudi z algebrskimi, transcendentalnimi številkami in tudi funkcijami različnega izvora, ki so povezane z aritmetiko teh številk. V teh študijah se poleg osnovnih in algebrskih metod uporabljajo tudi analitične in geometrijske metode. Natančneje, študija praštevil, vključenih v teorijo števil.

Prvotne številke so "gradniki" naravnih števil.

V aritmetiki obstaja teorem, ki se imenuje glavni. Po njenem mnenju je lahko vsako naravno število, razen enega, predstavljeno kot produkt, katerega faktorji so preproste številke, zaporedje faktorjev pa je edinstveno, to pomeni, da je način predstavitve edinstven. Imenuje se dekompozicija naravnega števila v osnovne faktorje. Za ta proces obstaja drugo ime - faktorizacija števil. Izhajajoč iz tega lahko preproste številke imenujemo „gradbeni material“, „bloki“ za gradnjo naravnih števil.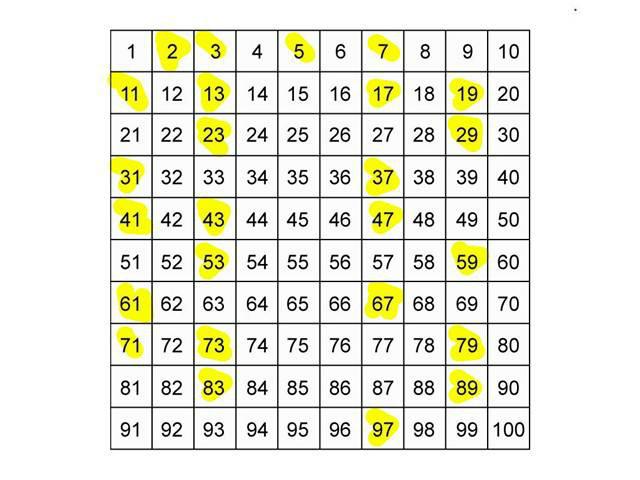

Išči prave številke. Preskusi enostavnosti

Mnogi znanstveniki različnih časov so poskušali najti nekaj načel (sistemov) za iskanje seznama prvih števil. Znanost pozna sisteme, ki se imenujejo sito Atkin, sito Sundartam in sito Eratosten. Vendar pa ne zagotavljajo nobenih pomembnih rezultatov in preprosta kontrola se uporablja za iskanje praštevil. Tudi matematiki so ustvarili algoritme. Imenujejo se testi enostavnosti. Na primer, Rabin in Miller sta razvila test. Uporabljajo ga kriptografi. Obstaja tudi Kayal-Agraval-Sasken test. Vendar pa je kljub zadostni natančnosti zelo težko izračunati, kar zmanjšuje njegovo praktično vrednost.

Ali ima množica primarnih številk omejitev?

Dejstvo, da je niz preprostih je neskončnost, je zapisano v knjigi "Načela" starodavnega grškega učenjaka Euclida. Rekel je to: »Predstavljajmo si za trenutek, da imajo praštevila omejitev. Potem jih pomnožimo med seboj in dodamo en izdelek. Število, ki ga dobimo kot rezultat teh preprostih dejanj, ne moremo razdeliti na eno od številnih praštevilk, ker bo vedno ostal v preostalem. In to pomeni, da obstaja še nekaj številk, ki še niso vključene v seznam osnovnih števil. Zato naša predpostavka ni resnična in ta sklop ne more imeti meje. Poleg dokazov Euclida obstaja tudi modernejša formula švicarskega matematika iz 18. stoletja Leonarda Eulerja. Po njegovem mnenju je vsota, ki je inverzna do vsote prvih n števil, naraščala brez omejitve, ko število n narašča. Ampak formula izreka o porazdelitvi primes: (n) raste kot n / ln (n).

Kaj je največje število primerov?

Vsekakor je Leonard Euler uspel najti največji premier za svoj čas. To je 2 ³¹ - 1 = 2147483647. Vendar pa je bila do leta 2013 izračunana druga najbolj natančna na seznamu prvih števil, 2 ^57885161 - 1, ki se imenuje Mersennova številka. Vsebuje približno 17 milijonov decimalnih mest. Kot lahko vidite, je število znanstvenikov iz 18. stoletja nekajkrat manjše od tega. To je moralo biti tako, ker je Euler ta izračun opravljal ročno, vendar je naš računalnik verjetno pomagal naš sodobnik. Poleg tega je bilo to število pridobljeno na fakulteti za matematiko na eni od ameriških fakultet. Številke, poimenovane po tem znanstveniku, preidejo po testu enostavnosti Luke-Lemere. Vendar se znanost na tem mestu ne želi ustaviti. Fundacija Electronic Frontier, ki je bila ustanovljena leta 1990 v Združenih državah Amerike (EFF), je imenovala denarno nagrado za iskanje velikih primerov. In če so do leta 2013 nagrado upoštevali znanstveniki, ki bi jih našli med 1 in 10 milijoni decimalnih števil, je danes ta številka dosegla od 100 milijonov do 1 milijarde. Velikost nagrad se giblje od 150 do 250 tisoč ameriških dolarjev.

Imena posebnih praštevil

Tiste številke, ki so bile najdene zahvaljujoč algoritmom, ki jih je ustvaril eden ali drug znanstvenik in so opravile preskus preprostosti, se imenujejo posebne. Tukaj je nekaj od njih:

1. Merssen.

2. Wooda.

3. Kmetija.

4. Cullen.

5. Prota.

6. Mills et al.

Enostavnost teh številk, poimenovanih po omenjenih znanstvenikih, je določena z uporabo naslednjih testov:

1. Luc-Lemer.

2. Pepin.

3. Rizel.

4. Billhart - Lemera - Selfridge itd.

Sodobna znanost se tu ne ustavi in ​​verjetno je, da bo v bližnji prihodnosti svet vedel imena tistih, ki bi lahko dobili nagrado v višini 250.000 dolarjev, pri čemer najdejo največje število.