Kako najti diamantni kvadrat? Možni načini za iskanje odgovora

Matematika je šolski predmet, ki ga vsi študirajo, ne glede na profil razreda. Vendar je vsi ne obožujejo. Včasih nepravično. Ta znanost nenehno vrže učencem naloge, ki omogočajo, da se njihovi možgani razvijajo. Matematika se odlično spopada, da otrokom ne dajo duševnih sposobnosti, da umrejo. Eden od njegovih delov se s tem sooča še posebej dobro - geometrijo.

Vse teme, ki jih preučujemo, so vredne pozornosti in spoštovanja. Geometrija je način za razvoj prostorske domišljije. Primer je tema kvadratov številk, zlasti diamantov. Te uganke lahko vodijo v slepo ulico, če ne razumete podrobnosti. Ker so možni različni pristopi k iskanju odgovora. Nekdo lažje zapomni različne različice formul, ki so napisane spodaj, in nekdo jih lahko dobi iz predhodno naučenega gradiva. V vsakem primeru se brezupne situacije ne zgodijo. Če pomislite malo, boste našli rešitev.

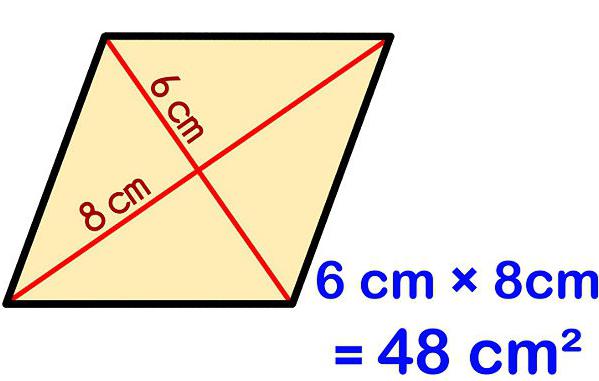
Kaj je romb in kako izgleda kot drugi štirikotniki?

Odgovorite na to vprašanje, da boste razumeli načela pridobivanja formul in potek razmišljanja v težavah. Konec koncev, da bi razumeli, kako najti območje romba, morate jasno razumeti, kakšna je slika in kakšne so njene lastnosti.

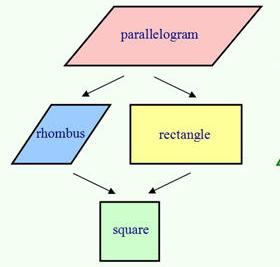
Za lažje upoštevanje paralelograma, ki je štirikotnik s parnimi stranmi, vzamemo "staršev". Ima dva "otroka": pravokotnik in romb. Oba sta paralelograma. Če nadaljujemo vzporednice, je to "priimek". Torej, da bi našli romb Uporabite lahko že preučeno formulo paralelograma.

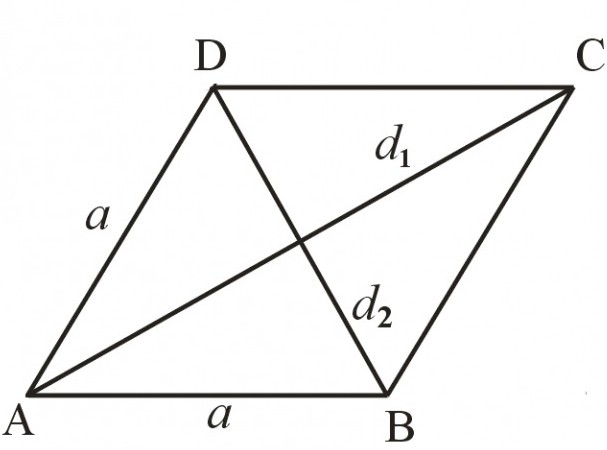
Ampak, kot vsi otroci, ima romb nekaj svojega. To se nekoliko razlikuje od "starševskega" in se lahko obravnava kot ločena številka. Navsezadnje pravokotnik ni romb. Če se vrnemo k vzporednicam, so kot brat in sestra. Imajo veliko skupnega, vendar se še vedno razlikujejo. Te razlike so njihove posebne lastnosti, ki jih je treba uporabiti. Čudno bi bilo vedeti o njih in ne bi se uporabljali pri reševanju problemov.

Če nadaljujemo analogijo in si zapomnimo še eno sliko - kvadrat, potem bo to nadaljevanje romba in pravokotnika. Ta številka združuje vse lastnosti enega in drugega.

Diamantne lastnosti

Obstaja jih pet in so navedene spodaj. Nekateri od njih ponavljajo lastnosti paralelograma, nekateri pa so neločljivo povezani z obravnavano sliko.

• Romb je paralelogram, ki je dobil posebno obliko. Iz tega sledi, da so njegove strani parno paralelne in enake. Poleg tega so v parih neenake in to je vse. Kot bi imel kvadrat.
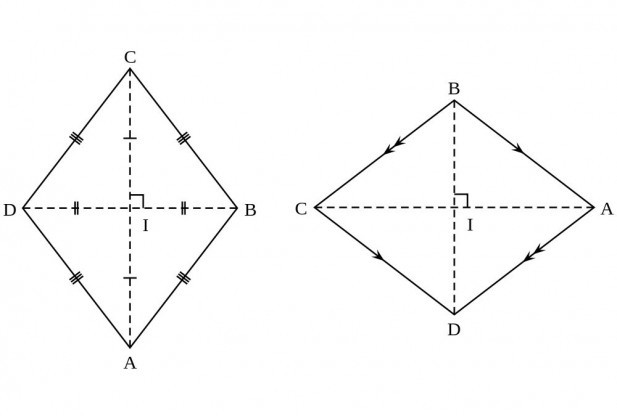
• Diagonali tega štirikotnika se sekajo pod kotom, ki je enak 90 °. To je priročno in zelo poenostavi potek razmišljanja pri reševanju problemov.
• Druga lastnost diagonal: vsaka od njih je razdeljena s presečiščem na enake segmente.
• Kota, ki ležita nasproti drug drugemu, sta enaka.
• In zadnja lastnost: diagonala romba se ujema z bisektorjem kotov.

Oznake, ki so sprejete v obravnavanih formulah

Pri matematiki je treba reševati probleme z uporabo skupnih črkovnih izrazov, ki se imenujejo formule. Tema trga ni izjema.

Da bi šli v evidenco, ki pove, kako najti območje diamanta, se morate strinjati s črkami, ki so nadomestile vse številske vrednosti elementov slike.

Zdaj je čas, da napišete formule.

Med podatki o nalogi so samo diagonalni diamanti.

Pravilo navaja, da moramo, da bi našli neznano količino, pomnožiti dolžine diagonal in nato produkt razdeliti na pol. Rezultat delitve je območje romba po diagonalah.

Formula za ta primer bo izgledala takole:

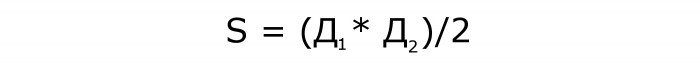
Pustite to formulo na številko 1.

Naloga je dana strani diamanta in njegovi višini

Če želite izračunati površino, morate najti izdelek teh dveh količin. Morda je to najpreprostejša formula. Poleg tega je iz teme o območju paralelograma znano. Tam je bila taka formula že proučena.

Pisanje matematike:

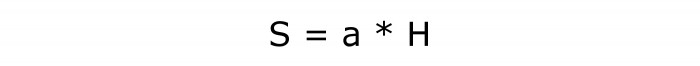
Številka te formule je 2.

Znana stran in oster kot

V tem primeru morate kvadratno velikost rombne strani. Nato poiščite sinus kota. Tretji korak je izračun produkta dveh nastalih količin. Odgovor bo diamantni kvadrat.

Literalni izraz:

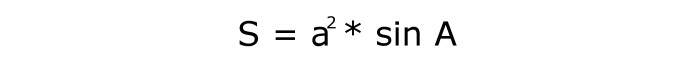
Njegova serijska številka je 3.

Te vrednosti: polmer vpisanega kroga in akutni kot

Če želite izračunati površino romba, morate najti kvadrat polmera in ga pomnožiti s 4. Določite vrednost sinusnega kota. Nato produkt razdelite na drugo količino.

Formula ima naslednjo obliko:

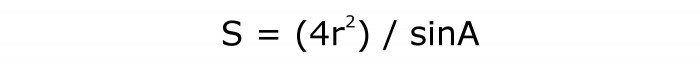
Oštevilčen bo 4.

Problem vključuje stran in polmer vpisanega kroga.

Če želite ugotoviti, kako najti območje romba, morate izračunati produkt teh količin in število 2.

Formula za to nalogo bo izgledala takole:

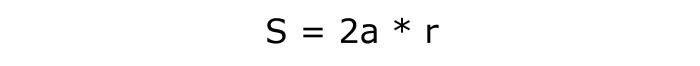
Njena številka je v redu - 5.

Primeri možnih nalog

Naloga 1

Eden od diagonal romba je 8, drugi pa 14 cm, potrebno pa je najti območje slike in dolžino njegove strani.

Rešitev

Da bi našli prvo vrednost, potrebujemo formulo 1, v kateri je D ₁ = 8, D ₂ = 14. Nato se površina izračuna na naslednji način: (8 * 14) / 2 = 56 (cm2).

Diagonali delijo diamant na 4 trikotnike. Vsak od njih bo pravokoten. To je treba uporabiti za določitev vrednosti druge neznane. Stran romba bo postal hipotenuza trikotnika, noge pa bodo polovica diagonal.

Potem a ² = (D _1/2 ) ² + (D 2/2) ² Po zamenjavi vseh vrednosti dobimo: a ² = (8/2) ² + (14/2) ² = 16 + 49 = 65. Toda to je kvadrat strani. Torej morate izvleči kvadratni koren od 65. Potem bo dolžina stranice približno enaka 8,06 cm.

Odgovor: površina je 56 cm ² , stran je 8,06 cm.

Naloga 2

Diamantna stran ima vrednost 5,5 dm, višina pa 3,5 dm. Poiščite območje slike.

Rešitev

Da bi našli odgovor, bo potrebna formula 2. V njej je a = 5.5, H = 3.5. Potem, ko zamenjamo črke v formuli s številkami, dobimo, da je želena vrednost 5,5 * 3,5 = 19,25 (dm ² ).

Odgovor: območje romba je enako 19,25 dm ² .

Naloga 3

Akutni kot romba je 60 °, manjša diagonala pa je 12 cm, zato je potrebno izračunati njegovo površino.

Rešitev

Da bi dobili rezultat, boste potrebovali številko formule 3. V njej bo namesto A 60 in vrednost a neznana.

Da bi našli stran romba, se morate spomniti sinusovega teorema. V pravokotnem trikotniku bo a hipotenuza, manjša noga je enaka polovici diagonale in kot je razdeljen na polovico (znano iz lastnosti, kjer je omenjena simetrala).

Nato bo stran a enaka zmnožku noge na sinusu kota.

Noga mora biti izračunana kot D / 2 = 12/2 = 6 (cm). Sinus (A / 2) je enak njegovi vrednosti za kot 30º, to je 1/2.

Z enostavnimi izračuni dobimo naslednjo vrednost rombne strani: a = 3 (cm).

Zdaj je območje produkt 3 ² in sinus 60 °, to je 9 * ()3) / 2 = (9√3) / 2 (cm2).

Odgovor: želena vrednost je (9√3) / 2 cm ² .

Rezultati: vse je mogoče

Tu so bile obravnavane nekatere možnosti za iskanje območja diamanta. Če v problemu ni jasno, katera formula je uporabljena, je treba malo razmisliti in poskušati povezati predhodno preučene teme. V drugih temah vedno obstaja namig, ki bo pomagal povezati znane vrednosti s tistimi v formulah. In problem bo rešen. Glavna stvar je, da se spomnimo, da se lahko vse, kar smo prej raziskali, uporabimo in moramo uporabiti.

Poleg predlaganih nalog so možne tudi inverzne težave, ko je na območju številke potrebno izračunati vrednost diamantnega elementa. Nato morate uporabiti enačbo, ki je najbližje pogoju. Nato pretvorite formulo in pustite neznano vrednost na levi strani enakosti.