Kako izračunati diagonalo prizme ravnega štirikotnika?

Prizma je geometrijska volumetrična figura, katere značilnosti in lastnosti se preučujejo v srednjih šolah. Praviloma se pri proučevanju upoštevajo količine kot volumen in površina. V tem članku bomo odprli nekoliko drugačno vprašanje: dajemo metodo za določanje dolžine prizemskih diagonal na primeru četverokotne oblike.

Katera številka se imenuje prizma?

V geometriji je podana naslednja definicija prizme: je tridimenzionalna oblika, omejena z dvema mnogokotnima identičnima stranema, ki sta vzporedni drug z drugim, in s številom vzporednic. Spodnja slika prikazuje primer prizme, ki ustreza tej definiciji.

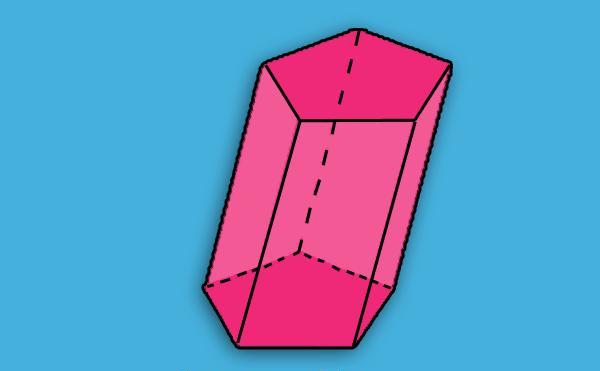
Vidimo, da sta dva rdeča peterokotnika enaka in sta v dveh vzporednih ravninah. Pet rožnatih paralelogramov poveže te pentagone v en predmet - prizmo. Dva peterokotnika se imenujejo podlage številke, vzporedni pa so stranski obrazi.

Prizme so ravne in poševne, prav tako imenovane pravokotne in poševne. Razlika med njima je v kotih med podnožjem in stranskimi površinami. Za pravokotno prizmo so vsi ti koti 90 ^° .

Glede na število strani ali vozlišč poligona na dnu govorijo o prizmah trikotne, peterokotne, štirikotne in tako naprej. In če je ta poligon pravilen in je sama prizma ravna črta, se taka oblika imenuje pravilna.

Prizma, prikazana na prejšnji sliki, je peterokotna. Spodaj je peterokotna ravna prizma, ki je pravilna.

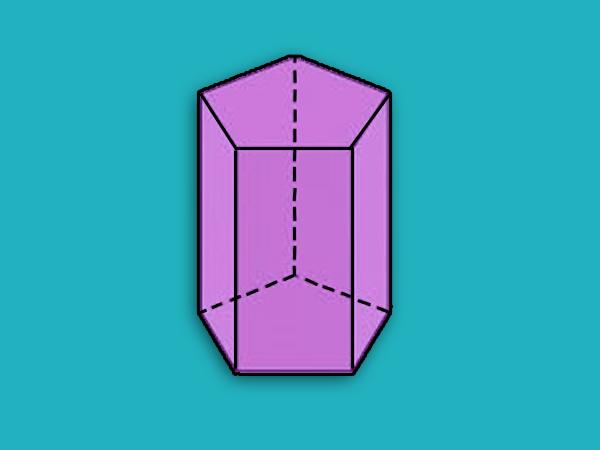
Vsi izračuni, vključno z metodo določanja diagonale prizme, je primerna za natančne rezultate.

Kateri elementi označujejo prizmo?

Elementi slike so sestavni deli, ki ga tvorijo. Posebej za prizmo obstajajo tri glavne vrste elementov:

• vrhovi;
• obrazi ali stranice;
• rebra.

Obrazi so baze in stranske ravnine, ki predstavljajo paralelograme v splošnem primeru. V prizmi je vsaka stran vedno ene od dveh vrst: bodisi poligon ali paralelogram.

Robovi prizme so tisti segmenti, ki omejujejo vsako stran slike. Tako kot robovi so tudi robovi dveh vrst: pripadajo osnovni in stranski površini ali pripadajo samo stranski površini. Prvi je vedno dvakrat večji od drugega, ne glede na vrsto prizme.

Točke so presečišča treh robov prizme, od katerih dve ležita v ravnini osnove, tretja pa pripada dvema stranskima stranema. Vse tocke prizme so v ravninah podlage slike.

Številke opisanih elementov so povezane v enotno enakost, ki ima naslednjo obliko:

P = B + C - 2.

Tu je P število robov, B - vrhov, C - strani. Ta enakost se imenuje Eulerjev izrek za polieder.

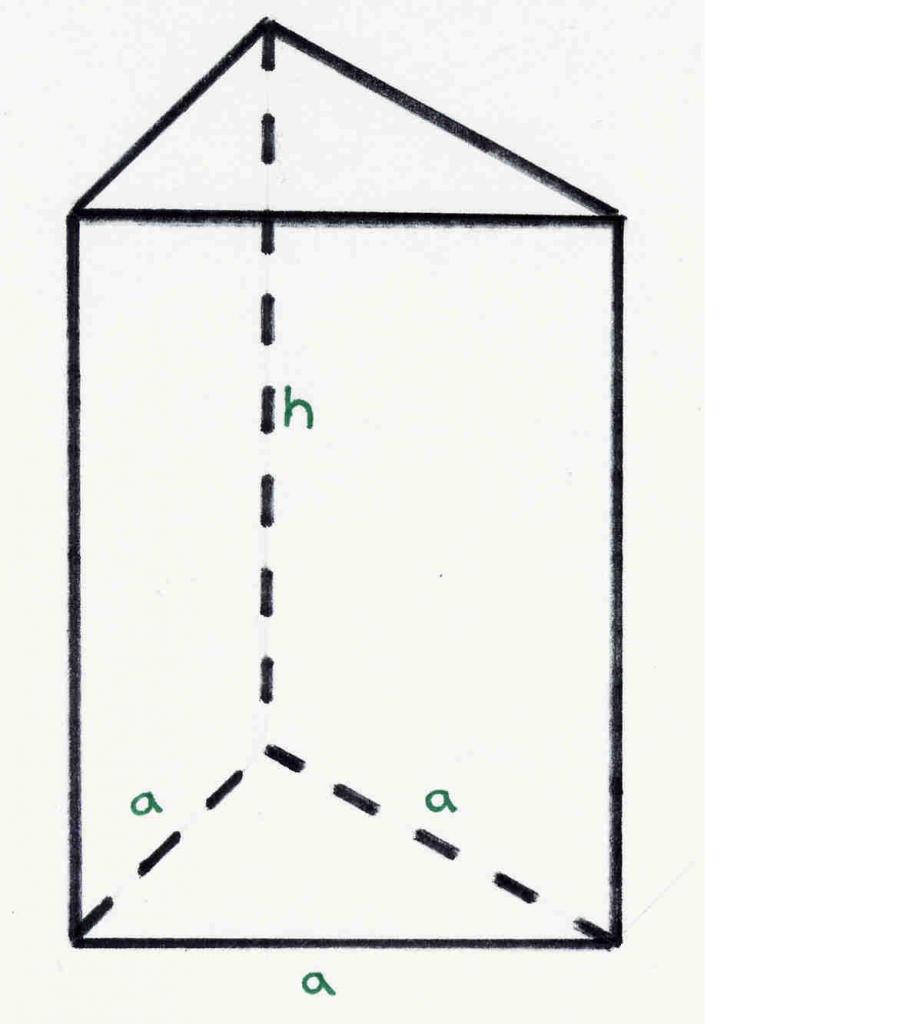
Slika prikazuje trikotno pravilno prizmo. Vsakdo lahko ugotovi, da ima 6 tock, 5 strani in 9 robov. Te številke so skladne z Eulerovim izrekom.

Diagonalne prizme

Po lastnostih, kot so volumen in površina, pri težavah v geometriji se pogosto najdejo informacije o dolžini dane diagonale obravnavane številke, ki je bodisi podana ali jo je treba najti z drugimi znanimi parametri. Razmislite, kaj je diagonala prizme.

Vse diagonale lahko razdelimo v dve vrsti:

1. Leži v ravnini obrazov. Povezujejo ne-sosednja vozlišča poligona na dnu prizme ali paralelogram stranske površine. Vrednost dolžin takih diagonal se določi na podlagi poznavanja dolžin ustreznih robov in kotov med njimi. Za določanje diagonal paralelogramov se vedno uporabljajo lastnosti trikotnikov.
2. Leži znotraj volumna prizme. Te diagonale povezujejo ne-enega-na-enega vrhov dveh baz. Te diagonale so popolnoma znotraj slike. Njihova dolžina je nekoliko težje izračunati kot za prejšnji tip. Metoda izračuna vključuje upoštevanje dolžin robov in osnove ter paralelograme. Za ravne in pravilne prizme je izračun razmeroma preprost, saj se izvaja z uporabo Pitagorovega izreka in lastnosti trigonometričnih funkcij.

Spodaj so prikazani primeri izračunavanja različnih diagonal.

Diagonalne stranice kvadratne ravne prizme

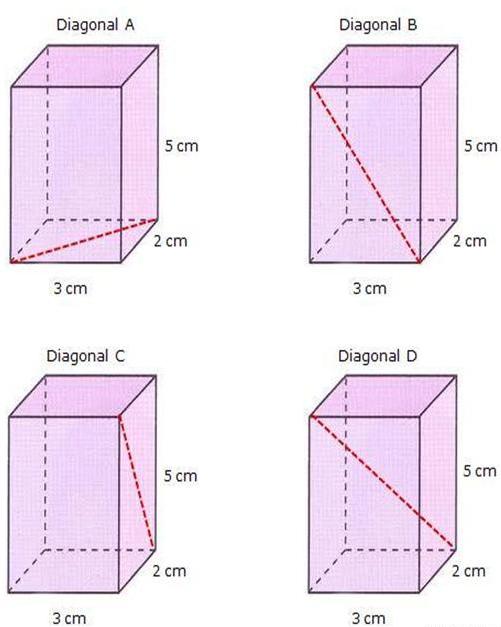
Zgornja slika prikazuje štiri enake ravne prizme in podane so parametri njihovih robov. Na prizmah diagonale A, diagonale B in diagonale C je rdeča črta prikazana diagonala treh različnih obrazov. Ker je prizma ravna z višino 5 cm, njena podlaga pa je pravokotnik s stranicami 3 cm in 2 cm, je težko najti označene diagonale. Za to uporabite Pitagorov izrek.

Dolžina diagonale osnove prizme (Diagonala A) je enaka:

D _A = √ (3 ² +2 ² ) = 13 ≈ 3,606 cm.

Za stransko stran prizme je diagonala (glej Diagonala B):

D _B = √ (3 ² + 5 ² ) = 34 ≈ 5.831 cm.

Nazadnje je dolžina druge diagonale strani enaka (glej Diagonal C):

D _C = √ (2 ² + 5 ² ) = 29 ≈ 5,385 cm.

Dolžina notranje diagonale

Zdaj izračunamo dolžino diagonale štirikotne prizme, ki je prikazana na prejšnji sliki (Diagonal D). To ni tako težko, če opazite, da je to hipotenuza trikotnika, v kateri je višina prizme (5 cm) in diagonala D _A, prikazana na sliki na levi zgoraj (Diagonala A), noge. Potem dobimo:

D _D = √ (D _A ² + 5 ² ) = √ (2 ² +3 ² +5 ² ) = 38 ≈ 6.164 cm.

Pravilna prizma štirikotna

Diagonala pravilne prizme, katere osnova je kvadrat, se izračuna na enak način kot v zgornjem primeru. Ustrezna formula je:

D = √ (2 * a ² + c ² ).

Kjer so a in c dolžine osnovne in stranske strani, sta.

Upoštevajte, da smo v izračunih uporabili le Pitagorov izrek. Da bi določili dolžine diagonal pravilnih prizm z velikim številom tock (peterokotno, heksagonalno in tako dalje), je potrebno uporabiti trigonometrične funkcije.