Kako izračunati kote med vektorji?

Pri proučevanju geometrije se pojavlja veliko vprašanj na temo vektorjev. Študent ima posebne težave pri iskanju kotov med vektorji.

Osnovni izrazi

Pred obravnavo kotov med vektorji se je treba seznaniti z definicijo vektorja in konceptom kota med vektorji.

Vektor je segment, ki ima smer, to je segment, za katerega je določen njegov začetek in konec.

Kot med dvema vektorjema na ravnini, ki ima skupni začetek, se imenuje manjši od kotov, s katerim želimo premakniti enega od vektorjev okoli skupne točke, do položaja, kjer se njihove smeri ujemajo.

Formula za reševanje

Ko razumemo, kaj je vektor in kako določimo njegov kot, lahko izračunamo kot med vektorji. Rešilna formula za to je precej preprosta in rezultat njene uporabe bo vrednost kosinusa kota. Po definiciji je enaka določenemu skalarnemu produktu vektorjev in produktu njihovih dolžin.

Skalarni produkt vektorjev se šteje kot vsota ustreznih koordinat faktorskih vektorjev, pomnoženih med seboj. Dolžina vektorja ali njegov modul se izračuna kot kvadratni koren iz vsote kvadratov njegovih koordinat.

Po pridobitvi vrednosti kosinusa kota se lahko velikost kota sam izračuna z uporabo kalkulatorja ali s pomočjo trigonometrične tabele.

Primer

Ko boste razumeli, kako izračunati kot med vektorji, bo rešitev ustreznega problema postala preprosta in enostavna. Kot primer je vredno razmisliti o enostavni nalogi iskanja velikosti kota.

Najprej bo bolj primerno izračunati potrebno za reševanje vrednosti dolžin vektorjev in njihovega skalarnega produkta. Z zgoraj opisanim opisom dobimo:

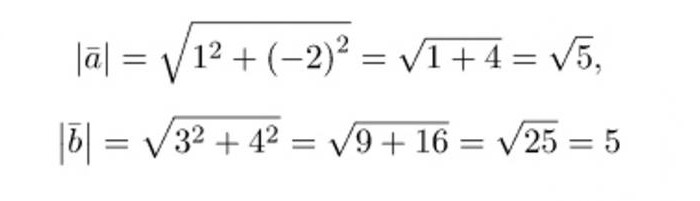
Z nadomestitvijo dobljenih vrednosti v formulo izračunamo kosinus želenega kota:

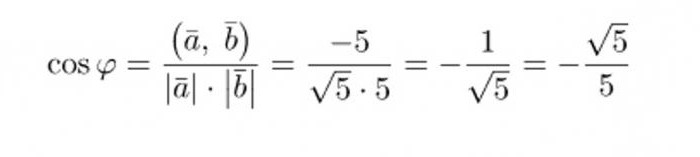
Ta številka ni ena od petih skupnih vrednosti kosinusa, zato, da bi dobili kot, boste morali uporabiti kalkulator ali trigonometrično tabelo Bradisa. Toda preden dobimo kot med vektorji, lahko formulo poenostavimo, da se znebimo dodatnega negativnega znaka:

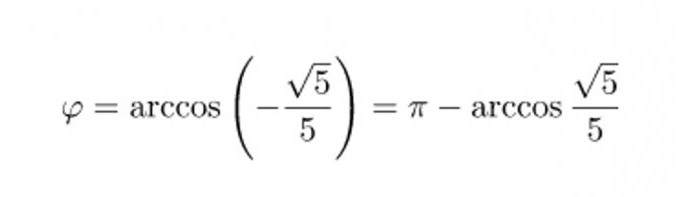
Končni odgovor za ohranjanje natančnosti lahko pustite v tej obliki in lahko izračunate kot v stopinjah. V skladu s tabelo Bradisa bo njegova vrednost približno 116 stopinj in 70 minut, kalkulator pa bo prikazal vrednost 116,57 stopinj.

Izračunajte kot v n-dimenzionalnem prostoru

Pri obravnavi dveh vektorjev v. T tridimenzionalni prostor veliko težje je razumeti, kateri kotiček je v nasprotju, če ne ležijo v isti ravnini. Za poenostavitev zaznavanja lahko narišete dva segmenta, ki se križata in tvorita najmanjši kot med njimi in bosta želena. Kljub prisotnosti tretje koordinate v vektorju se proces, kako se izračunajo koti med vektorji, ne bo spremenil. Izračunajte skalarni izdelek in module vektorjev, lok kosinus njihovega zasebnega in boste odgovor na to težavo.

V geometriji so pogosto težave s prostori, ki imajo več kot tri dimenzije. Za njih pa algoritem za iskanje odgovora izgleda enako.

Razlika med 0 in 180 stopinj

Ena izmed najpogostejših napak pri pisanju odgovora na problem, ki je bil zasnovan za izračun kota med vektorji, je odločitev, da se zapiše, da so vektorji vzporedni, to je, da je bil želeni kot 0 ali 180 stopinj. Ta odgovor je napačen.

Po pridobitvi vrednosti kota 0 stopinj po rezultatih odločitve bi bil pravilen odgovor označiti vektorje kot usmerjene, to pomeni, da bodo vektorji imeli isto smer. V primeru 180 stopinj bodo vektorji nasprotno usmerjeni.

Posebni vektorji

Če najdemo kote med vektorji, lahko najdemo enega od posebnih tipov, poleg tistih, ki so opisani zgoraj.

• Več vektorjev, ki so vzporedni eni ravnini, se imenujejo koplanarni.
• Vektorji enake dolžine in smeri se imenujejo enaki.
• Vektorji, ki ležijo na eni premici, ne glede na smer, se imenujejo kolinearni.
• Če je dolžina vektorja enaka nič, to pomeni, da se njen začetek in konec ujemata, potem se imenuje nič in če je en, potem je enota.