Višja matematika: ravnina v prostoru
Drugi po ravni črti je pomemben element prostorske geometrije ravnina. Sposobnost opisa z enačbo omogoča izračun prostorskih kotov in višin za različne tridimenzionalne oblike. V tem članku podajamo vse vrste enačb, ki opisujejo ravnino v prostoru. Upoštevajte tudi možne možnosti za medsebojno razporeditev letal.
Geometrijski koncept ravnine
V dvodimenzionalni geometriji se ravnina ne upošteva, saj so vsi problemi rešeni le v koordinatah x in y. Ko dodamo tretjo koordinatno os z, postane ravnina pomemben geometrični element.
Izraz "ravnina" se razume kot zbirka točk, od katerih je vsaka dva, če je povezan, dobljeni vektor vedno pravokoten na določen vektor. Ta dani vektor se imenuje normalno. Normalna igra pomembno vlogo pri numeričnem opisu ravnine in njene lastnosti se uporabljajo za reševanje različnih problemov.
Spodnja slika prikazuje tri ravnine v prostoru (modro), ki se sekajo četrtega (rdečega).
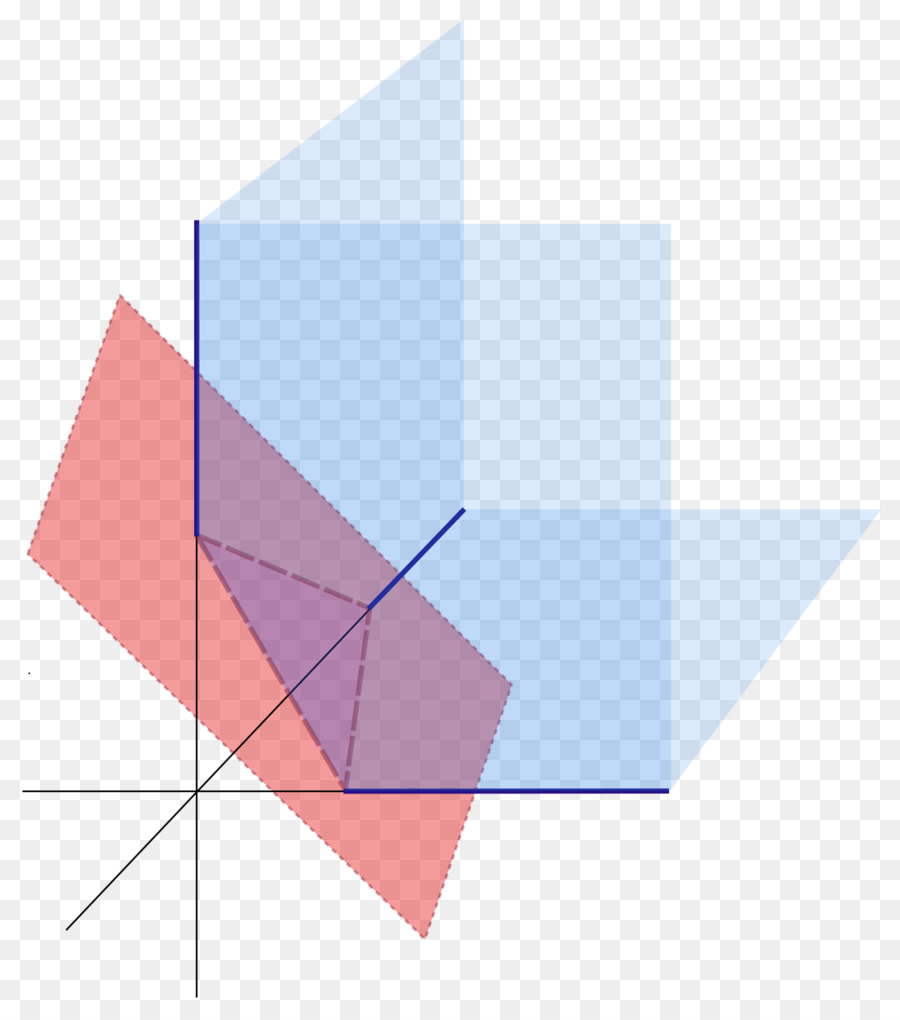
Splošna enačba
Zgornja definicija bo pomagala pridobiti enačbo za ravnino v prostoru v koordinatah. Recimo, da obstaja točka z znanimi koordinatami Q (x 0 ; y 0 ; z 0 ). Znano je, da leži v določeni ravnini, katere norma je enaka n¯ (A; B; C). Predpostavimo, da prav temu pripada tudi poljubna točka M (x; y; z). Slednje pomeni, da bodo vektorji QM¯ in n¯ pravokotni, to pomeni, da njihov skalarni izdelek izgine. Zato lahko napišemo naslednjo enakost:
(QM¯ * n¯) = 0.
Če nadomestimo koordinate in odpremo oklepaje, pridemo do enačbe:
(xx 0 ) * A + (yy 0 ) * B + (zz 0 ) * C = 0 =>
A * x + B * y + C * z + D = 0, kjer je D = -1 * (A * x 0 + B * y 0 + C * z 0 ).
Dobljena enačba za ravnino se imenuje splošna. Ima enako obliko kot splošna enačba za neposredno enačbo na ravnini. Vidimo lahko, da koeficienti, ki se soočajo s spremenljivkami x, y in z, niso nič drugega kot koordinate pravokotne ravnine vektorja. Imenuje se režija.
Upoštevajte, da če je pri pridobivanju splošne enačbe določena točka Q neznana in obstaja le smerni vektor np, potem pridemo do enačbe za niz vzporednih ravnin, ki se razlikujejo le v parametru D.
Delna enačba
Pri upodabljanju ravnin v prostoru, ko so podane specifične osi koordinat, je najlažje vzdrževati geometrijske konstrukcije, če obstajajo točke, kjer ravnina seka te osi. Izraz, ki vam omogoča, da ugotovite koordinatne vrednosti preseka ravnine z osmi x, y in z, se imenuje intervalna enačba. To je mogoče doseči z izvedbo nekaterih matematičnih transformacij s splošno enačbo.
Recimo, da je znana naslednja enačba:
A * x + B * y + C * z + D = 0.
Prosti izraz D prenesemo na desno stran enačbe in nato razdelimo obe strani enačbe tako, da je enota na desni. Imamo:
A * x + B * y + C * z = -D =>
x / (- D / A) + y / (- D / B) + z / (- D / C) = 1 ali
x / p + y / q + z / r = 1, kjer je p = -D / A, q = -D / B, r = -D / C.
Nastali izraz se imenuje enačba v segmentih, dolžine segmentov, ki so odrezani na osi x, y in z, začenši od točke (0; 0; 0), imajo vrednosti p, q in r. To lahko preverimo na naslednji način: če predpostavimo, da so koordinate vzdolž osi y in z enake nič, potem dobimo x enako q. To pomeni, da ima sečišče s osjo x koordinate (p; 0; 0). Podobno trdimo, da dobimo še dve koordinati (0; q; 0) in (0; 0; r).
Parametrična vektorska enačba
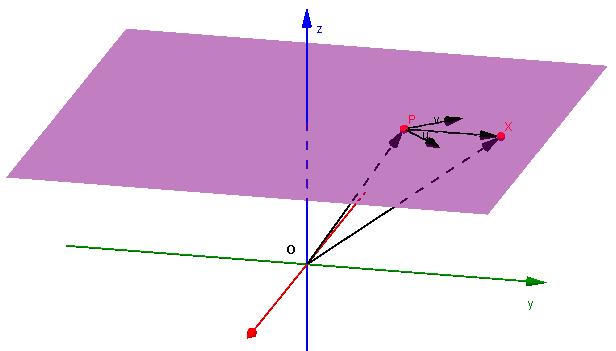
To je tretja pomembna vrsta enačbe, ki se pogosto uporablja tudi pri reševanju problemov. Zgoraj je bilo prikazano, da je ravnina enolično določena s točko in normalnim vektorjem. Vendar pa je mogoče ta geometrični dvodimenzionalni objekt določiti na drugačen način.
Recimo, da obstajata dva koplanarna vektorja, ki nista vzporedna. Označujemo jih z u ¯ (a 1 ; b 1 ; c 1 ) in v¯ (a 2 ; b 2 ; c 2 ). Znana je tudi točka Q (x 0 ; y 0 ; z 0 ). Kakšna bo enačba ravnine, ki gre skozi to točko in dva vektorja?
Na to vprašanje lahko odgovorite tako, da dobite enačbo na splošno. Vendar bomo ta problem rešili na drug način. Spomnimo se, da lahko katerikoli vektor ravnine razgradimo na dva druga koplanarna vektorja, ki prav tako pripadata tej ravnini. To pomeni, da lahko poljuben vektor QP¯, kjer je P (x; y; z), predstavimo kot:
QP¯ = α * u¯ + β * v¯.
Skozi vse točke P ravnine dobimo ustrezne parametre α in β. Enačba, podana za ravnino, se imenuje parametrična vektorska. Pogosto je posneta v koordinatni obliki:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a 1 ; b 1 ; c 1 ) + β * (a 2 ; b 2 ; c 2 ).
Vidimo lahko, da je ta oblika pisanja ravnine podobna vektorski enačbi za premico v dvodimenzionalnih in tridimenzionalnih primerih.
Ta izraz lahko tudi bolj izrecno zapišete z ločevanjem spremenljivk:
x = x 0 + a * a 1 + β * a 2 ;
y = y 0 + α * b 1 + β * b 2 ;
z = z 0 + α * c 1 + β * c 2 .
Te tri enačbe imajo obliko, ki je podobna parametrični enačbi za ravno črto v prostoru. Ta tip se pogosto uporablja pri pretvarjanju vektorske enačbe v skupno za ravnino.
Vzporedne ravnine
Obstajata samo dve možnosti za relativni položaj dveh ravnin v vesolju. V tem delu članka podajamo pogoj, ko so vzporedni.
Če sta obe enačbi ravnine podani v splošni obliki, je njuna paralelnost precej preprosta. Dve ravnini bosta vzporedni, če sta njuni vektorji taka vodila. Recimo, da obstajata dve enačbi:
A 1 * x + B 1 * y + C 1 * z + D 1 = 0;
A 2 * x + B 2 * y + C 2 * z + D 2 = 0.
Pravokotno na vsako ravnino vektorja so koordinate:
n 1 ¯ (A1; B1; C1);
n 2 ¯ (A 2 ; B 2 ; C 2 ).
Če lahko vektor n 1 ¯ predstavimo kot množenje z realnim številom vektorja n 2 ¯, potem bosta oba paralelna, to je:
n 2 ¯ = l * n 1 ¯, kjer je l realno število.
Drug način za določitev njihovega paralelizma je iskanje kosinusa kota med njimi preko skalarnega produkta in modulov vektorjev. Ta kosinus mora biti enak enoti, potem bodo vektorji (ravnine) vzporedni. Ustrezna formula je:
cos (φ) = | (n 1 ¯ * n 2 ¯) | / (| n 1 ¯ | * | n 2 ¯ |) = 1.
Če so enačbe ravnin podane v parametrični vektorski obliki, potem je vzporednost v prostoru ravnin določena tudi iz pogoja vzporednosti normalov z njimi. Da bi našli smerne vektorje teh normalov, moramo vzeti vektorske produkte vektorjev, ki tvorijo vsako ravnino.
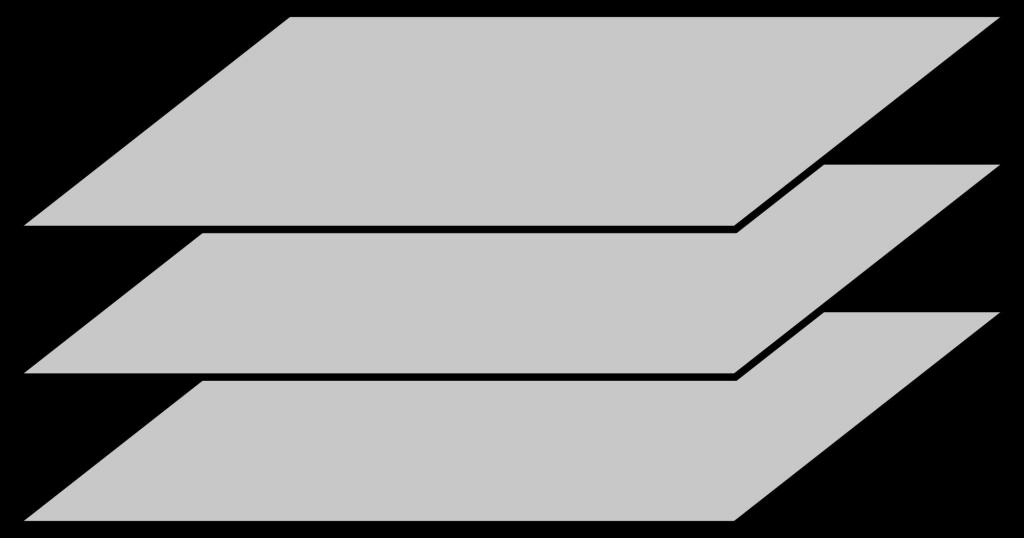
Zgornja slika prikazuje tri ravnine, ki so vzporedne.
Presečje ravnin
To je druga različica medsebojne ureditve v prostoru ravnin. V tem primeru se dve ravnini sekajo vzdolž neke ravne črte, ki jim pripada. V tem primeru je pomembno, da lahko izračunamo kot diedernega preseka tega preseka. Vedno je enak kotu med ustreznimi vodilnimi vektorji, to je med navpičnicama ravnin.
V prejšnjem odstavku je že podana formula, ki omogoča izračun kota med normali. Tu jo bomo odprli le s pisanjem koordinat vektorjev n 1 ¯ in n 2 ¯:
ar = arccos (| A 1 * A 2 + B 1 * B 2 + C 1 * C 2 | / (√ (A 1 2 + B 1 2 + C 1 2 ) * √ (A 2 2 + B 2 2 + C 2 2 ))).
Ta formula se pogosto uporablja pri izračunu dihedralnih kotov med ravninami piramide ali poševne prizme.
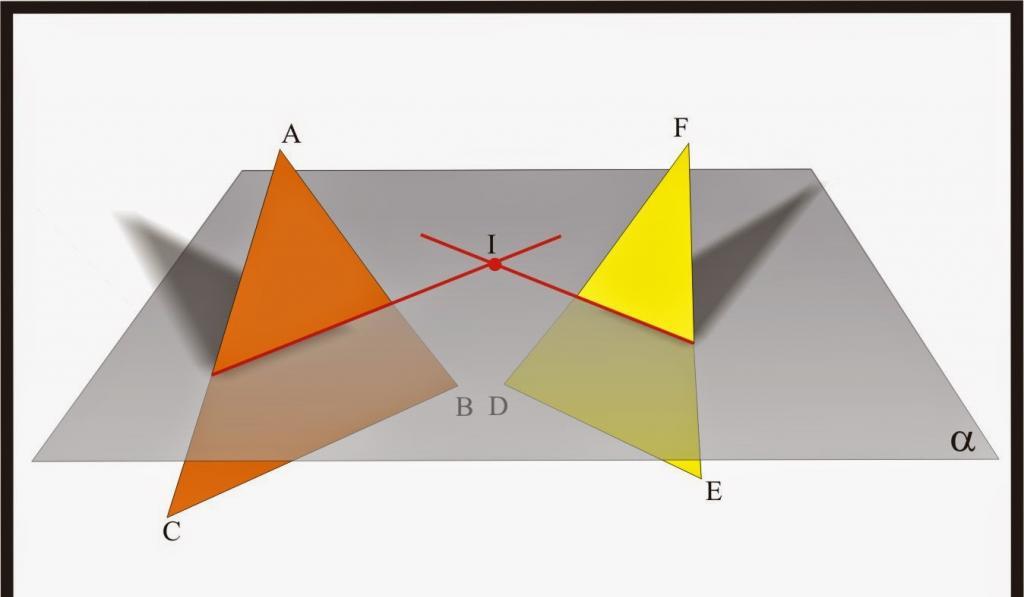
Na zgornji sliki sta prikazani dve ravnini, ki sekajo tretji horizontali.
Poseben primer preseka dveh ravnin je kot φ = 90 o , to je pravokotnost obravnavanih geometrijskih objektov. Za določitev pravokotnosti ni potrebno izračunati kota φ z nekoliko bolj zapleteno formulo zgoraj, zato bo dovolj izračunati vrednost skalarnega izdelka n 1 ¯ in n 2 ¯. Za pravokotne ravnine je nič, to je:
(n 1 ¯ * n 2 ¯) = A 1 * A 2 + B 1 * B 2 + C 1 * C 2 = 0.
Snop letal
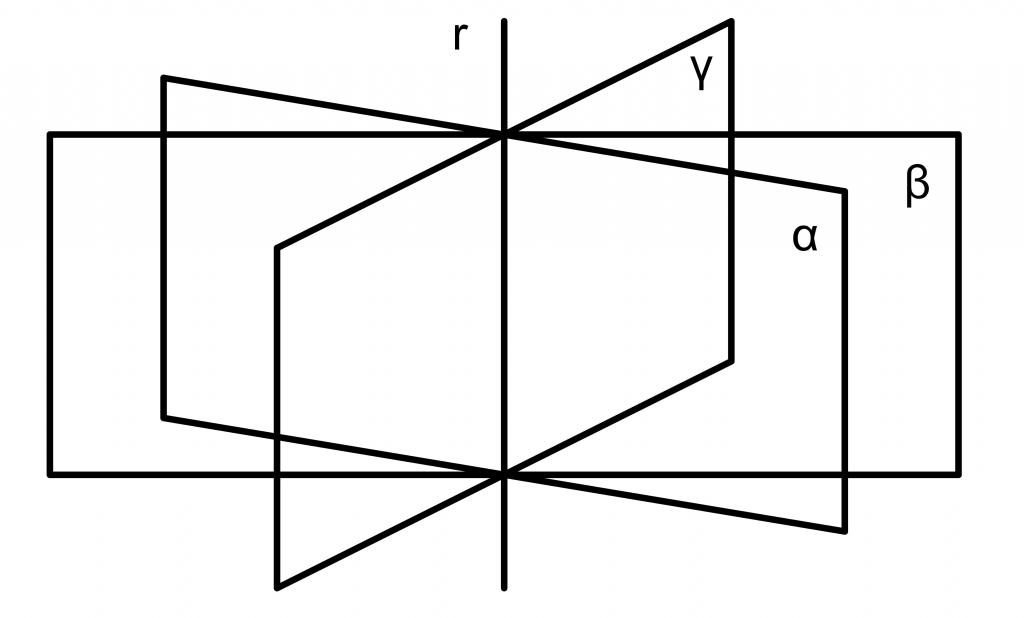
Če se dve ravnini križata, vse njihove skupne točke ležijo na eni premici. Upoštevajte, da je ena od metod za določanje ravne črte v prostoru sistem dveh splošnih enačb ravnine. Koliko ravnin v prostoru lahko potegnete skozi eno ravno črto? Neskončno število. Njihova zbirka se imenuje sveženj. Enačba, ki opisuje ta sveženj, ima naslednjo obliko:
k 1 * (A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Tu sta k 1 in k 2 poljubne številke. Poseben primer je situacija, ko en ali oba parametra k ne moreta prevzeti vrednosti nič. Recimo, da je k 1, 0, potem lahko enačbo žarka prepišemo v obliki:
(A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 / k 1 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Ta enakost opisuje vse ravnine žarka, razen ene, ki ima neposredni vektor n 2 ¯ (A 2 ; B 2 ; C 2 ).
Primer snopa ravnin je zbirka listov odprte knjige.

Nato rešujemo več geometrijskih problemov z uporabo pridobljenega znanja o lastnostih ravnin v prostoru.
Pretvorite parametrično vektorsko enačbo v splošno
Glede na naslednjo ravninsko enačbo v parametričnem vektorskem obrazcu:
(x; y; z) = (1; 2; 0) + α * (1; 2; 3) + β * (- 1; 3; 0).
To je potrebno napisati kot splošno enačbo ravnine v prostoru.
Izrecno ga prepišite:
x = 1 + α - β;
y = 2 + 2 * α + 3 * β;
z = 3 * α.
Iz zadnjega izraza dobimo α, nato ga nadomestimo v prvo enakost in izrazimo β. Najdeni parametri so zamenjani v drugo enačbo, imamo:
α = z / 3;
β = 1 - x + z / 3;
y = 2 + 2 * z / 3 + 3 - 3 * x + z =>
y + 3 * x + 5/3 * z - 5 = 0 =>
9 * x + 3 * y + 5 * z -15 = 0.
Za pridobitev splošne enačbe iz parametričnega vektorja jo moramo najprej izrecno zapisati, nato pa parametre izraziti v smislu spremenljivih koordinat.
Pretvorba splošnega v parametrično vektorsko enačbo
Ta naloga je popolnoma nasprotna prejšnji. Razmislite o tehnikah za njegovo rešitev.
Glede na naslednjo enačbo:
x-2 * y + 3 * z -1 = 0.
Za začetek naj bo ena koordinata izražena v dveh. Express npr. X:
x = 2 * y-3 * z +1.
To pomeni, da vsaka točka, ki ima koordinate, pripada ravnini:
(2 * y-3 * z +1; y; z).
Sedaj bomo to koordinato prepisali kot vsoto treh vektorjev, prva bo vsebovala le spremenljivko y, druga pa samo z, tretja pa bo sestavljena samo iz številk. Imamo:
(x; y; z) = (2 * y; y; 0) + (-3 * z; 0; z) + (1; 0; 0).
Vidimo, da pri odpiranju te enačbe dobimo splošne koordinate za točko ravnine. Zdaj je ostalo le še faktorizirati spremenljivke v prvem in drugem vektorju in jih redefinirati s parametri α in β. Dobimo:
(x; y; z) = (1; 0; 0) + α * (2; 1; 0) + β * (- 3; 0; 1).
Pridobili smo enačbo v parametrični vektorski obliki, podobni prvotni.
Slika ravnine v koordinatnem sistemu
Naloga je naslednja: po znani enačbi je treba v prostoru narisati ravnino. Ustrezna enačba je:
3 * x - y -4 * z +5 = 0.
Za prikaz te ravnine je treba poiskati točke, na katerih seka koordinatne osi. V ta namen lahko dobimo ustrezno enačbo v segmentih. Vendar pa v tem primeru nadaljujemo drugače: postavimo dve koordinati, ki sta enaki nič, in izračunamo tretjo. Imamo:
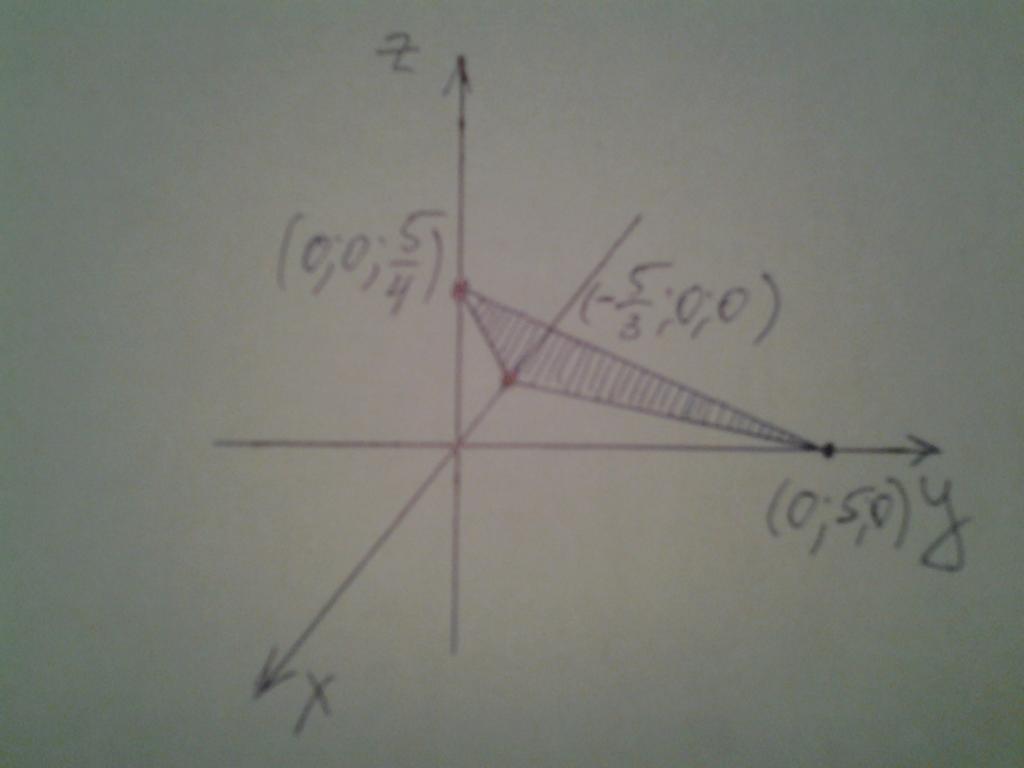
y = 0; z = 0; x = -5/3;
x = 0; z = 0; y = 5;
x = 0; y = 0; z = 5/4.
Preostale točke je treba postaviti na koordinatne osi in skozi njih narisati ravnino. Položaj ravnine v prostoru je prikazan na spodnji sliki.
Tri točke in ravnina
Naj se dajo tri točke v prostoru:
M (l; -1; 3);
N (3, 2, -4);
L (2; 5; 0).
Potrebno je najti ravnino, ki teče skozi njih.
Iz geometrije je znano, da tri točke, ki ne ležijo na eni premici, enolično določajo ravnino. Njegovo enačbo lahko sestavimo, če najdemo njeno vektorsko vodilo n. To je enako vektorskemu produktu koplanarnih vektorjev, ki ležijo v ravnini. Koordinate vektorjev lahko dobimo iz koordinat točk, na primer:
MN¯ (2; 3; -7);
ML¯ (1; 6; -3).
Njihov vektorski izdelek bo dal vektor n¯. Izračunamo ga:
n¯ (33; -1; 9).
Če vzamemo na primer točko M, dobimo splošno enačbo v obliki:
33 * x -y + 9 * z - 61 = 0.
Koordinate točk N in L lahko nadomestite z enačbo in se prepričajte, da je enakost enaka.