Štiri formule, s katerimi lahko izračunate površino romba. Diamantne lastnosti

Romb je posebna figura v geometriji. Zaradi svojih posebnih lastnosti ni ene, ampak več formul, s pomočjo katerih se izračuna površina romba. Kakšne so te lastnosti in katere so najpogostejše formule za iskanje območja te številke? Poglejmo.

Katero geometrijska oblika imenovan diamant

Preden ugotovite, kaj je območje romba, je vredno vedeti, kakšna je to številka.

Od časa evklidske geometrije se romb imenuje simetrični štirikotnik, katerega vse štiri stranice so enake v dolžini in vzporedne v parih.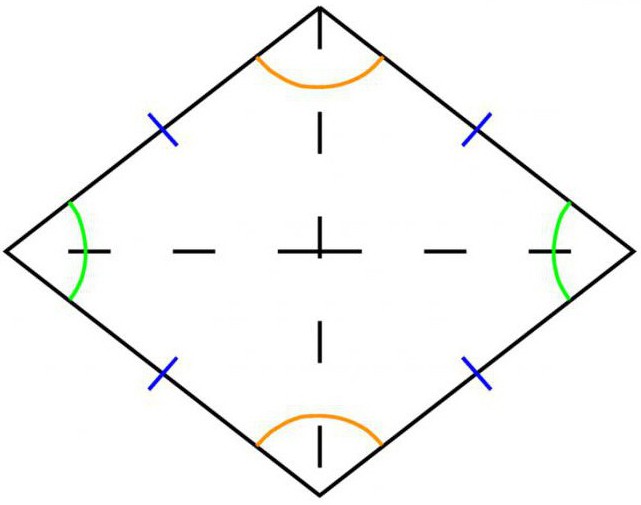

Izvor izraza

Ime te številke je prišlo do najsodobnejših jezikov iz grščine, preko mediacije latinščine. "Prednik" besede "romb" je postal grški samostalnik μόμβος (tamburin). Čeprav so si prebivalci dvajsetega stoletja, navajeni na okrogle tamburine, težko predstavljati drugačno obliko, vendar pa so Heleni tradicionalno te glasbene instrumente naredili ne okrogle, ampak diamantne oblike.

V večini sodobnih jezikov se ta matematični izraz uporablja kot v latinščini: rombus. V angleščini pa se diamanti včasih imenujejo diamant (diamant ali diamant). Ta podoba je dobila ta vzdevek zaradi svoje posebne oblike, ki spominja na dragi kamen. Praviloma se tak izraz ne uporablja za vse diamante, ampak samo za tiste, katerih kot presečišča med obema stranema je šestdeset ali štirideset pet stopinj.

Prvič je bila ta številka omenjena v spisih grškega matematika, ki je živel v prvem stoletju nove dobe - čaplje Aleksandrijske.

Katere lastnosti ima ta geometrijska figura?

Da bi našli območje romba, morate najprej vedeti, kakšne značilnosti ima ta geometrijska figura.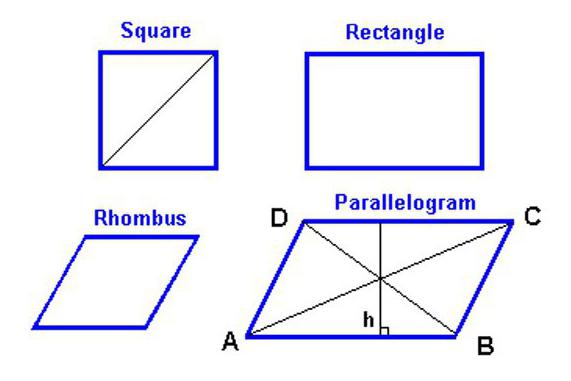

• Kot je že omenjeno v definiciji romba, je štirikotnik. In zato, ker so njegove nasprotne strani v parih medsebojno vzporedne, se lahko romb imenuje tudi paralelogram, kar pomeni, da se večina lastnosti te številke nanaša nanj.
• Oba diagonalna romba na njegovem presečišču sta enakomerno razdeljena na dva dela. Zaradi tega, ker se križajo pod kotom 90 stopinj, diagonali delijo sliko na 4 pravokotni trikotnik.
• V vsakem rombu diagonali delijo njegove kote na dva dela, hkrati pa so tudi bisektorji.
• Če se vsaka od dveh diagonal romba dvigne na moč kvadrata, bo njihova vsota enaka zmnožku kvadrata strani te številke in števila štiri.
• Če povežete črte na sredini štirih strani romba, bo dobljena slika pravokotnik.
• Če je krog vpisan v diamant (ne glede na njegove kote), bo njegova osrednja točka sovpadala s presečiščem diagonal.
• Diagonalni diamanti v stiku z osmi simetrije pri kotih 90 stopinj.
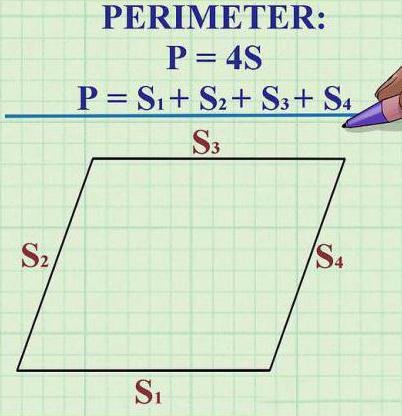
• Ker so vse strani romba enake med seboj po dolžini, se njen obseg izračuna po formuli P = 4 x K (K je dolžina ene od strani).

Pod kakšnimi pogoji je paralelogram diamant

Kot veste, je vsak romb paralelogram, toda ne vsak paralelogram je romb. Da bi lahko natančno trdili, da je predstavljena figura dejansko romb in ne preprost paralelogram, mora ustrezati eni od treh glavnih značilnosti, ki razlikujejo romb. Ali vse tri naenkrat.

1. Diagonalni paralelogram se križa pod kotom 90 stopinj.
2. Diagonali delijo kote na dva dela in delujejo kot bisektorji.
3. Ne samo vzporedno, temveč tudi sosednje strani imajo enako dolžino. To je, mimogrede, ena glavnih razlik med rombom in paralelogramom, saj ima druga številka le vzporedne strani, ne pa sosednjih.

Pod kakšnimi pogoji je romb kvadrat

Glede na njegove lastnosti lahko v nekaterih primerih romb hkrati postane kvadrat. Če želite jasno potrditi to izjavo, preprosto zavrtite kvadrat v obe smeri za štirideset pet stopinj. Dobljena slika bo diamant, katerega kot je devetdeset stopinj.

Če želite potrditi, da je kvadrat romb, lahko primerjate znake teh številk: v obeh primerih so vse strani enake, diagonale pa bisektrike in sekajo pod kotom 90 stopinj.

Kako najti območje romba s pomočjo diagonal

V sodobnem svetu na internetu lahko najdete skoraj vse materiale za izvedbo potrebnih izračunov. Torej obstaja množica virov, opremljenih s programi za samodejno izračunavanje območja določene oblike. Še več, če (kot v primeru romba) obstaja več formul za to, potem obstaja možnost, da izberete, katera od njih je najbolj primerna za uporabo. Najprej pa je potrebno, da lahko brez kompjuterja izračunamo površino romba in se usmerimo v formule. Za diamant jih je veliko, vendar so najbolj znane štiri.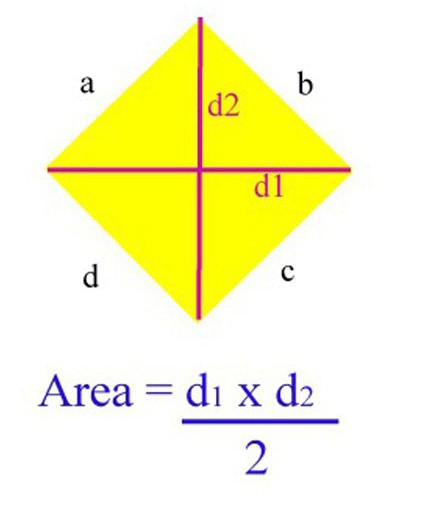

Eden od najlažjih in najpogostejših načinov za ugotovitev območja te številke, če obstajajo informacije o dolžini njegovih diagonal. Če ima problem te podatke, lahko v tem primeru uporabimo naslednjo formulo, da najdemo območje: S = KM x LN / 2 (KM in LN sta diagonala rombov KLMN).

V praksi lahko preverite veljavnost te formule. Predpostavimo, da ima KLMN romb eno diagonalo KM, njegova dolžina je 10 cm, drugi LN pa 8 cm, nato te podatke nadomestimo z zgornjo formulo in dobimo naslednji rezultat: S = 10 x 8/2 = 40 cm ² .

Formula za izračun površine paralelograma

Obstaja še ena formula. Kot že omenjeno v definiciji romba, ni le štirikotnik, ampak tudi paralelogram in ima vse značilnosti te oblike. V tem primeru je smiselno uporabiti formulo, uporabljeno za paralelogram: S = KL x Z. V tem primeru je KL dolžina vzporednega dela (romb), Z pa dolžina višine, ki je narisana na to stran.

Pri nekaterih nalogah dolžina strani ni podana, vendar je obod diamanta znan. Ker je formula za iskanje zgoraj navedena, jo lahko uporabimo za ugotavljanje dolžine stranice. Torej je obod številke 10 cm, stranska dolžina pa se lahko prepozna tako, da se obrne formulo za obod in razdeli 10 na 4. Rezultat je 2,5 cm - to je želena dolžina rombne strani.

Zdaj je vredno poskusiti nadomestiti to število v formuli, vedoč, da je dolžina na stran tudi 2,5 cm, zdaj pa bomo skušali te vrednosti postaviti v zgoraj omenjeno formulo paralelograma. Izkaže se, da je površina romba S = 2,5 x 2,5 = 6,25 cm2.

Drugi načini za izračun Diamond Area

Tisti, ki so že obvladali sinuse in kosinus, lahko uporabijo formule, ki jih vsebujejo, da bi našli območje romba. Klasičen primer je naslednja formula: S = KM ² x Sin KLM. V tem primeru je območje slike enako zmnožku obeh strani romba, pomnoženo s sinusom kota med njimi. In ker so v rombu vse strani enake, je lažje takoj izdelati eno stran v kvadrat, kot je prikazano v formuli.

To shemo preverjamo v praksi in ne samo na rombu, temveč na kvadrat, ki ima, kot je dobro znano, vse kotne ravne, kar pomeni, da so 90 stopinj. Recimo, da je ena stran 15 cm, znano pa je tudi, da je sinus kota 90 °. Nato po formuli S = 15 x 15 x Sin 90 ° = 255x1 = 255 cm2 ^.

Poleg zgoraj navedenega se v nekaterih primerih uporablja tudi druga formula, ki uporablja sinus za določitev območja romba: S = 4 x R ² / Sin KLM. Pri tej varianti se uporablja polmer kroga, vpisanega v diamant. Dvigne se na moč kvadrata in pomnoži s štiri. Celoten rezultat delimo s sinusom kota, ki je v bližini vpisane številke.

Na primer, za enostavnost izračunov bomo ponovno vzeli kvadrat (sinus njegovega kota bo vedno enak enemu). Polmer kroga, v katerega je vtisnjen, je 4,4 cm, nato se izračuna površina rombov: S = 4 x 4,4 ² / Sin 90 ° = 77,44 cm ²

Zgornje formule za iskanje polmera romba so daleč od edinstvenih, vendar so najlažje razumeti in izvajati izračune.