Ekstremne funkcije. Kako najti?
Matematična analiza - to je precej zabaven del matematike, s katerim se soočajo absolutno vsi diplomanti in študenti. Kljub temu, ne vsi imajo radi matan. Nekateri morda ne razumejo niti osnovnih stvari, kot je navidezno standardna študija funkcije. Ta članek je namenjen odpravi takšne napake. Želite izvedeti več o analizi funkcije? Želite vedeti, kaj so točke ekstremov in kako jih najti? Potem je ta članek za vas.
Študija grafov funkcij
Najprej je vredno razumeti, zakaj je graf sploh potrebno analizirati. Obstajajo preproste funkcije za risanje, ki ni težko. Parabola lahko služi kot jasen primer take funkcije. Nariši njen urnik ni težko. Vse, kar je potrebno, je, da poiščemo številke, za katere funkcija z enostavnim preoblikovanjem prevzame vrednost, in načeloma je to vse, kar je potrebno za risanje, da bi narisali graf parabole.
Kaj pa, če je funkcija, katere graf, ki jo moramo narisati, veliko težje? Ker so lastnosti kompleksnih funkcij precej nejasne, je potrebno izvesti celotno analizo. Samo takrat lahko funkcijo prikažemo grafično. Kako to storiti? Odgovor na to vprašanje najdete v tem članku.
Načrt analize funkcij
Prva stvar, ki jo je treba storiti, je izvedba površne študije funkcije, v kateri bomo našli področje definicije. Torej začnimo z redom. Domena definicije je zbirka vrednosti, za katere je določena funkcija. Preprosto povedano, to so številke, ki se lahko uporabijo v funkciji namesto x. Da bi določili obseg, morate le pogledati vnos. Očitno je na primer, da je funkcija y (x) = x 3 + x 2 - x + 43 domena definicije množica realnih števil. No, s funkcijo, kot je (x 2 - 2x) / x, je vse malo drugače. Ker število v imenovalcu ne sme biti 0, bo področje funkcije vse realne številke, poleg ničle.
Nato morate poiskati ti funkcijske ničle. To so vrednosti argumenta, za katerega celotna funkcija prevzame vrednosti nič. Da bi to naredili, je potrebno funkcijo enačiti z ničlo, podrobno jo preučiti in izvesti nekaj transformacij. Vzemimo funkcijo y (x) = (x 2 - 2x) / x, ki nam je že znana. Iz šolskega tečaja vemo, da je frakcija 0, ko je števec nič. Zato zavržemo imenovalec in začnemo delati s števcem in ga izenačimo z ničlo. Dobimo x 2 - 2x = 0 in postavimo x za oklepaje. Zato je x (x - 2) = 0. Kot rezultat, ugotovimo, da je naša funkcija nič, kadar je x enak 0 ali 2.
Ekstremne točke na grafu funkcije
Pri proučevanju grafa funkcije se mnogi srečujejo s problemom v obliki točk ekstremov. In to je čudno. Navsezadnje so skrajnosti precej preprosta tema. Ne verjameš? Prepričajte se sami z branjem tega dela članka, v katerem bomo govorili o točkah minimuma in maksimuma.
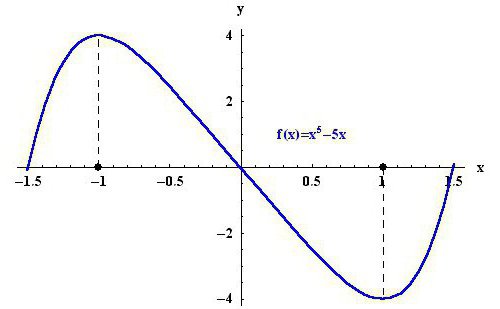
Če želite začeti, morate razumeti, kaj predstavlja skrajnost. Ekstrem je mejna vrednost, ki jo funkcija doseže na grafu. Od tu se izkaže, da obstajata dve skrajni vrednosti - maksimum in minimum. Za jasnost si lahko ogledate zgornjo sliko. V preučevanem območju je točka -1 največja vrednost funkcije y (x) = x 5 - 5x, točka 1 pa je minimalna.
Prav tako ne zamenjujte konceptov. Ekstremne točke funkcije so tisti argumenti, pri katerih dano funkcijo prevzame ekstremne vrednosti. Po drugi strani pa je ekstrem vrednost minimumov in maksimumov funkcije. Ponovno preglejte sliko zgoraj. -1 in 1 sta ekstremni točki funkcije, 4 in 4 pa sta sami skrajnosti.
Iskanje ekstremnih točk
Toda kako lahko najdemo ekstremne točke funkcije? Preprosto je. Prva stvar, ki jo je treba narediti, je, da najdemo derivat enačbe. Recimo, da imamo nalogo: "Poiščite ekstremne točke funkcije y (x), x je argument. Za jasnost vzamemo funkcijo y (x) = x 3 + 2x 2 + x + 54. Diferenciramo in dobimo naslednjo enačbo: 3x 2 + 4x + 1. Na koncu smo dobili standard kvadratna enačba. Naslednja naloga je, da jo enačimo z ničlo in najdemo korenine. Ker je diskriminantni večji od nič (D = 16 - 12 = 4), je ta enačba definirana z dvema korenima. Poiščite jih in dobite dve vrednosti: 1/3 in -1. To bodo ekstremne točke funkcije. Vendar, kako ugotoviti, kdo je kdo? Katera točka je najvišja in katera je minimalna? Če želite to narediti, vzemite naslednjo točko in ugotovite njeno vrednost. Na primer, vzemite številko -2, ki je levo od koordinatne črte od -1. To vrednost nadomestimo z enačbo y (-2) = 12 - 8 + 1 = 5. Posledično dobimo pozitivno število. To pomeni, da se na intervalu od 1/3 do -1 funkcija poveča. To pa pomeni, da se v intervalih od minus neskončnosti do 1/3 in od -1 do neskončnosti funkcija zmanjša. Tako lahko sklepamo, da je število 1/3 najmanjša točka funkcije na preučevanem intervalu, -1 pa je največja točka.
Vsota skrajnih točk funkcije

Omeniti je treba tudi, da je na USE potrebno najti samo točke ekstremov, ampak tudi opraviti nekakšno operacijo z njimi (dodajanje, množenje, itd.). Zato je treba posebno pozornost nameniti pogojem problema. Konec koncev lahko zaradi nepazljivosti izgubite točke.