Dirichletov princip: problemi z rešitvami
Obstaja veliko načel v matematiki. Nekateri so preprosti in razumljivi tudi za začetnike, nekateri pa zahtevajo določena pojasnila in dokaze. Vendar pa so vsi zelo učinkoviti in jih je mogoče zlahka uporabiti v praksi. Eden od njih je Dirichletov princip (znan tudi kot načelo golobov / zajcev). To je dokaj preprosta izjava, ki lahko pomaga pri reševanju mnogih matematičnih problemov.

Zgodovina
To načelo je leta 1834 oblikoval častni nemški matematik Johann Dirichlet. Danes se uporablja tako v kombinatoriki kot tudi v matematični fiziki. Prevedeno iz prvotnega nemškega, zveni kot "načelo škatel". Znanstvenik je opravil svoje raziskave z zajci in zabojniki. Pokazal je, da če navedemo, recimo, 5 kuncev v 7 posodah, potem bi vsaj ena posoda imela 5/7 ene živali. Vendar kunca ni mogoče razdeliti na dele, zato bo vsaj ena celica prazna (5/7 je 0 celih števil). Na enak način, v nasprotni smeri, če ima 7 kuncev in 5 škatel, ima vsaj eden od njih 2 kunca (7/5 je 2 nedotaknjena). Iz te izjave je matematika uspela oblikovati načelo, ki že vrsto let zagotavlja uspešno reševanje matematičnih problemov.
Sodobno besedilo in dokaz
Danes obstaja več različnih formulacij tega načela. Najbolj razumljivo in preprosto pomeni, da je nemogoče posaditi 8 kuncev v 3 kletke, tako da vsaka nima več kot 2. Bolj znanstvena in kompleksna formulacija, ki pojasnjuje Dirichletov princip, pravi: če v k celicah obstaja k + 1 kuncev, potem vsaj Vsaj ena celica bo vsebovala več kot en zajček. Če je v k-celicah tudi k-1 zajcev, bo vsaj ena celica vsebovala manj kot en zajček. Dokaz te trditve je preprosto, tako rekoč, protislovje. Če predpostavimo, da je v vsaki celici manj zajcev kot k-1 / k, je k zajčjih celic manjši od k * k-1 / k = k-1, kar je v nasprotju z začetnimi pogoji.
Pravzaprav tako preprosto in razumljivo načelo zelo olajša reševanje problemov iz matematike in dokazuje številne težavne izreke. Potrebno je le upoštevati, da se lahko zajci in celice enostavno zamenjajo z matematičnimi predmeti in predmeti (številke, točke, segmenti, številke itd.).
Drugo besedilo
Včasih naloge na Dirichletovem načelu niso tako preproste in očitne kot pri živalih v škatlah. To načelo je treba prenesti v matematične sklope, da bi našli rešitve. V tem primeru se lahko zanesete na drugačno, bolj zapleteno formulacijo. 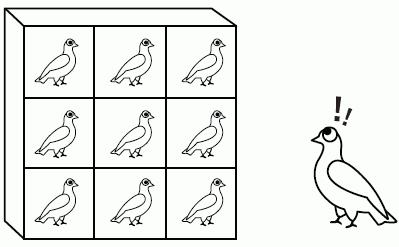
Če preslikamo množico S, ki vsebuje d + 1 elemente, v množico R z množico elementov d, potem bosta dva elementa iz množice S imela isto sliko.
Čeprav moderna GEF v matematiki nalaga kreativne zahteve študentom in ponuja nestandardne možnosti, rešitev z Dirichletovo trditvijo ni vedno tako preprosta in enostavna. Včasih je zelo težko določiti, katero vrednost je treba obravnavati kot žival, in ki je kot kletka in kako dejstvo, da imajo dve živali v eni kletki, pomaga rešiti problem. In če nam uspe ugotoviti, je še vedno nemogoče ugotoviti, v kateri celici bo objekt. To pomeni, da lahko preprosto dokažete obstoj takšne celice, vendar je ne morete konkretizirati.
Primer številka 1. Geometrija
Sodobni primeri reševanja problemov kažejo, da lahko popolni različni matematični predmeti delujejo kot živali in celice.
Naloga
Proga k poteka skozi ravnino trikotnika ABC, vendar se ne seka nobenega od njegovih tock. Treba je dokazati, da ne more prečkati svojih treh strani.
Rešitev
Predstavljajte si, kako linija k deli trikotnik na dve ravnini, naj jim rečemo s1 in s2. Predvidevamo, da sta s1 in s2 odprta, torej ne vsebuje črte k. No, zdaj je čas, da uporabimo Dirichletovo načelo. Naloge z rešitvami lahko pokažejo, da v sodobnih razmerah zajci in celice pomenijo različne predmete. Torej namesto zajcev nadomestimo tocke trikotnika in namesto celic - polovično ravnino. Ker vlečena črta k ne seka nobenega od tock, je vsak od njih v eni ali drugi ravnini. Ker pa v trikotniku obstajajo tri tocke in imamo samo dve ravnini (s1 in s2), bo ena izmed njih vsebovala dve tocki. Denimo, da so to vozlišča A in B in sta v pol-ravnini s2 (to je, da ležita na isti strani k). V tem primeru segment AB ne seka ravne črte k. To pomeni, da je stran v trikotniku, da k ne seka.
Alternativna rešitev
V tem problemu smo predpostavili, da sta točki A in B v isti ravnini, vendar Dirichletov princip ne navaja specifične celice, zato lahko tudi poudarimo, da so tocki C in B, ali A in C locirani v isti ravnini. ni pomembno, na kateri strani trikotnika je premica k seka. Zato je to načelo idealno za njegovo rešitev.
Primer št. 2. Geometrija
Naloga
V sredini enakostraničnega trikotnika ABC (v katerem je AB = BC = AC = 1) je bilo lociranih 5 točk. Dokazati je treba, da sta dve od njih oddaljeni manj kot 0,5.
Rešitev
Če v desnem trikotniku ABC narišete srednje črte, ga razdelimo na 4 majhna pravokotna trikotnika s stranicami ½ = 0,5. Recimo, da so ti trikotniki celice, točke v njih pa so zajci. Izkazalo se je, da imamo 5 kuncev in 4 celice, zato bomo v enem od njih našli vsaj dva kunca. Glede na to, da točke niso točke (ker se nahajajo znotraj trikotnika ABC in ne na eni od njenih strani), bodo postavljene znotraj majhnih številk. Zato bo razdalja med njimi manjša od 0,5 (ker velikost segmenta znotraj trikotnika nikoli ne presega velikosti njegove največje strani).
Primer številka 3. Kombinatorika
Na drugih področjih lahko uspešno uporabimo tudi Dirichletov princip: kombinatorika in matematična fizika že dolgo temeljijo na reševanju problemov.
Naloga
Na primer, okoli okrogle mize, m zastave različnih držav stojijo na enaki razdalji drug od drugega, in m predstavniki iz vsake države sedijo za mizo, vsaka od njih se nahaja poleg zastave nekoga drugega. Treba je dokazati, da bosta z določeno rotacijo mize vsaj dva izmed predstavnikov blizu svojih zastav.
Rešitev
Izkazalo se je, da so m-1 načini za razširitev tabele tako, da se medsebojna ureditev predstavnikov in zastav spremeni (če izključimo začetno postavitev tabele), vendar je m m predstavnikov levo.
Mi uporabimo Dirichletovo trditev za rešitev in označimo, da so predstavniki zajci, in nekateri položaji tabel med rotacijo so celice. V tem primeru je treba narediti analogijo med lokacijo zastopnika poleg ustrezne zastave in polnimi celicami. To pomeni, da je pozitiven rezultat (1 predstavnik nameščen v bližini njegove zastave) enakovreden rezultatu »kunec je v kletki«. Razumemo, da imamo eno celico manj, kot je potrebno (m-1), kar pomeni, da bo eden od njih imel vsaj 2 kunca. Hkrati pa ni izključeno, da bodo nekatere kletke prazne (noben predstavnik ne ustreza zastavi), v nekaterih kletkah pa bosta dva, tri ali celo več zajcev (dva, tri ali več predstavnikov bo sovpadlo z zastavami). Tako se bosta z eno določeno rotacijo vsaj dva predstavnika znašla blizu svojih zastav (vsaj dva zajca padejo v eno celico).
Z začetkom reševanja takega problema je pomembno razumeti, da je začetni položaj tudi celica, vendar je glede na stanje problema očitno prazen, zato zmanjšujemo skupno za 1 (m-1).
Primer številka 4. Teorija števil
Dirichletovo načelo v teoriji števil je prav tako bistvenega pomena.
Naloga
Recimo, na kosu zvezka v kletki, študent naključno v vozliščih celic položi 5 točk. Treba je dokazati, da vsaj en odsek z vozlišči na teh točkah poteka skozi vozlišče celice.
Rešitev
Najprej morate prikazati na listu zvezka koordinatni sistem, katerega osnova se nahaja v enem od vozlišč. Osi koordinatnega sistema bodo sovpadale z mrežnimi linijami, stran celice pa kot en segment. Izkazalo se je, da bo vseh 5 označenih točk v sistemu, njihove koordinate pa bodo samo celo število (parno ali liho). Tako dobimo 4 možnosti koordinat: (celo, celo), (liho, celo), (parno, liho) in (liho; liho). Tako bo 2 od 5 točk ustrezalo eni različici. Če pogledate situacijo iz Dirichletovega položaja, potem morate označiti točke kot zajce in koordinatne možnosti - kot celice. Dobimo 5 ptic z enim kamnom in 4 kletkami, v enem izmed njih bosta vsaj 2 živali. Denimo, da so to točke P in A, s koordinatami (x 4 , y 3 ) in (x 5 , y 6 ). Sredina segmenta, ki povezuje ta dva tocka, bo imel koordinate ((x 4 + x 5 ) / 2), ((y 3 + y 6 ) / 2)), ki bodo pod pogoji ustrezne paritete x 4 in x 5 cela števila , y 3 in y 6 . Izkazalo se je, da se sredina segmenta nahaja v vozlišču celic.
Primer številka 5
Z Dirichletovim načelom je mogoče rešiti precej nalog različne kompleksnosti. Težave z reševanjem različnih matematičnih in logičnih vprašanj se pogosto opirajo na to načelo.
Naloga
Na ravni cesti so kopali majhne prečne utore. Razdalja med vsemi utori je enaka in enaka Ö2 m. Potrebno je dokazati, da bo, ne glede na širino utorov, oseba, ki hodi po cesti v intervalih 1 m, enkrat padla v eno od njih.
Rešitev
Da bi olajšali rešitev, si je treba zamisliti, da se lahko cesta „navije“ na krog dolžine Ö2 metra. Izkaže se, da se bodo vsi žlebovi združili v dva nasproti, stopnji osebe pa bodo prikazani v obliki loka, ki je enaka 1 m. Zaporedoma moramo označiti vse korake, dokler eden od njih ni v loku, ki označuje utor, ne glede na dolžino k lok (širina utora). Seveda je očitno, da če bi človek hodil z razdaljo, ki je bila manjša od k, potem bi prej ali slej vstopil v jarek. Navsezadnje oseba ne more prestopiti razdalje k, če je njegova dolžina koraka manjša od k. Torej moramo poiskati dve stezi, razdalja med katero ne bo presegla vrednosti k. Za to bi bilo primerno uporabiti načelo Dirichleta. Mentalno razdelimo celoten krog na loke, ki so manjše od k in jih bomo obravnavali kot celice. Recimo, da jih je n. Predpostavimo, da je število korakov večje od števila lokov (n + m), čeprav zaradi iracionalnosti števila ,2 dva koraka ne sovpadata, potem pa bo v skladu z Dirichletovim načelom vsaj ena od celic vsebovala več kot en korak. Ker je dolžina loka manjša od k, bo razdalja med koraki manjša. Zato smo našli korake, potrebne za dokaz. 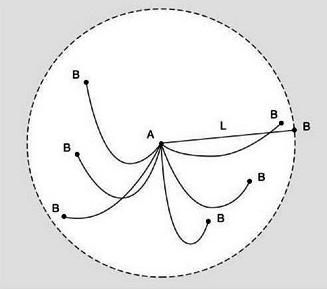
Posplošitev načela
Materiali za matematiko poleg standardnih (preprostih in ne zelo) formulacij vsebujejo tudi eno generalizirano, ki se uporablja za identifikacijo več kot dveh predmetov, ki sta si podobni. Trdi, da če so dm + 1 zajci dani v d celice, potem bo v isti celici vsaj m + 1 zajcev.
Primer št. 6. Generalizacija
Naloga
Pravokotnik s površino 5 x 6 celic (30 celic), osenčen samo 19. Ali je mogoče najti kvadrat s površino 2 x 2 celic, v katerih bodo vsaj tri barve prebarvane?
Rešitev
Naša slika mora biti razdeljena na 6 blokov po 5 celic. Na podlagi izjave Dirichleta bodo v eni izmed njih poslikane vsaj 4 celice (19/6 = 4). Nato v enem izmed kvadratov s površino 4 celic, ki se nahajajo v enem od blokov, bodo prebarvali vsaj 3 celice.
Primer številka 7
Razred, v katerem je 25 ljudi. Od treh naključno izbranih študentov bosta dva prijatelja. Treba je dokazati, da je v razredu šolar, ki ima več kot 11 prijateljev.
Dve rešitvi

Za začetek vzamemo dva učenca, ki nista drug z drugim prijateljska (če bi bili vsi med seboj prijatelji, bi bili v vsaki trojici trije prijatelji in vsak učenec bi bil prijatelj s 24 drugimi). Preostalih 23 sošolcev bo prijatel z enim od naših dveh, saj bi sicer prišlo do trojke brez prijateljev (kar je v nasprotju s prvotnim stanjem problema). Izkazalo se je, da bo eden od dveh študentov prijatelj z vsaj 12 študenti. V tem primeru so študenti zajci, izrazi "prijatelji ali ne" pa so celice. Imamo 23 živali in samo 2 kletke. V skladu s tem je v enem od njih vsaj 23/2 = 11,5, to je 12 zajcev. To pomeni, da bo eden od dveh študentov, ki jih bomo izbrali, prijatelji vsaj 12 njihovih sošolcev (ali celo več). Seveda obstajajo še druge metode za reševanje problema, vendar je to eden najbolj razumljivih in priročnih.